Lecture 4 OUTLINE Resistors in series equivalent resistance

Lecture #4 OUTLINE • Resistors in series – equivalent resistance – voltage-divider circuit – measuring current • Resistors in parallel – equivalent resistance – current-divider circuit – measuring voltage • Examples • Node Analysis Reading Chapter 2 EE 40 Fall 2004 Lecture 4, Slide 1 Prof. White

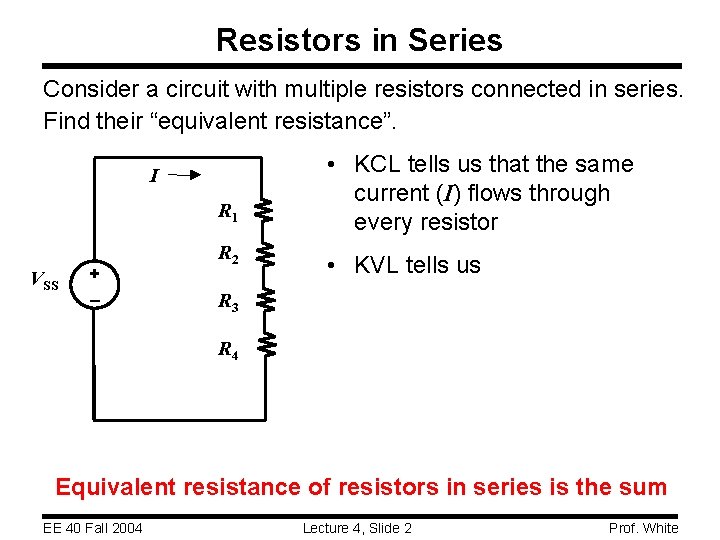
Resistors in Series Consider a circuit with multiple resistors connected in series. Find their “equivalent resistance”. I R 1 VSS + R 2 • KCL tells us that the same current (I) flows through every resistor • KVL tells us R 3 R 4 Equivalent resistance of resistors in series is the sum EE 40 Fall 2004 Lecture 4, Slide 2 Prof. White

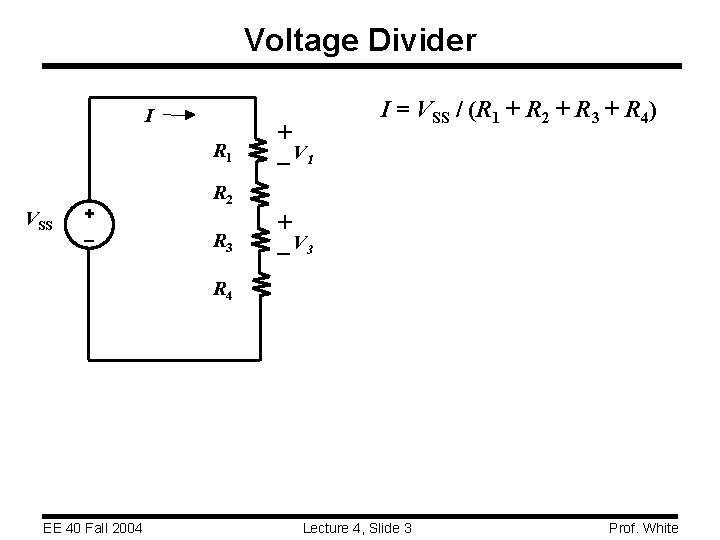
Voltage Divider I R 1 VSS + + – V 1 I = VSS / (R 1 + R 2 + R 3 + R 4) R 2 R 3 + – V 3 R 4 EE 40 Fall 2004 Lecture 4, Slide 3 Prof. White

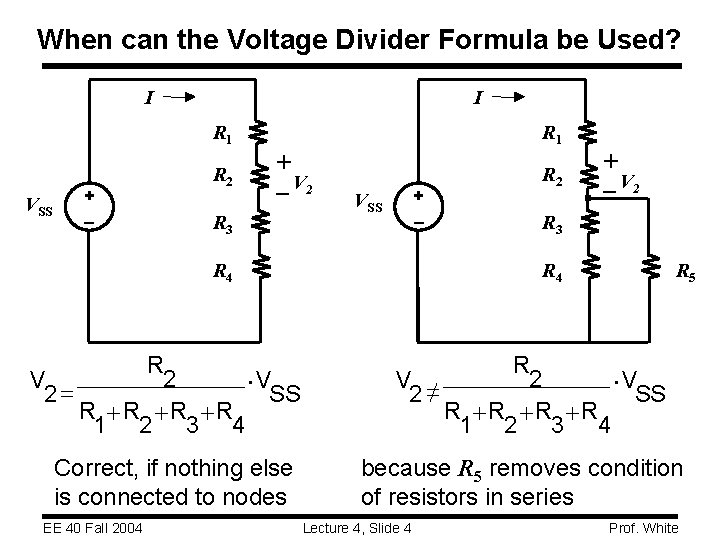
When can the Voltage Divider Formula be Used? I I R 1 VSS + R 2 R 1 + – V 2 R 3 + VSS R 4 R 2 V = ×V 2 SS R +R +R +R 1 2 3 4 Correct, if nothing else is connected to nodes EE 40 Fall 2004 R 2 + – V 2 R 3 R 4 R 5 R 2 V ≠ ×V 2 SS R +R +R +R 1 2 3 4 because R 5 removes condition of resistors in series Lecture 4, Slide 4 Prof. White

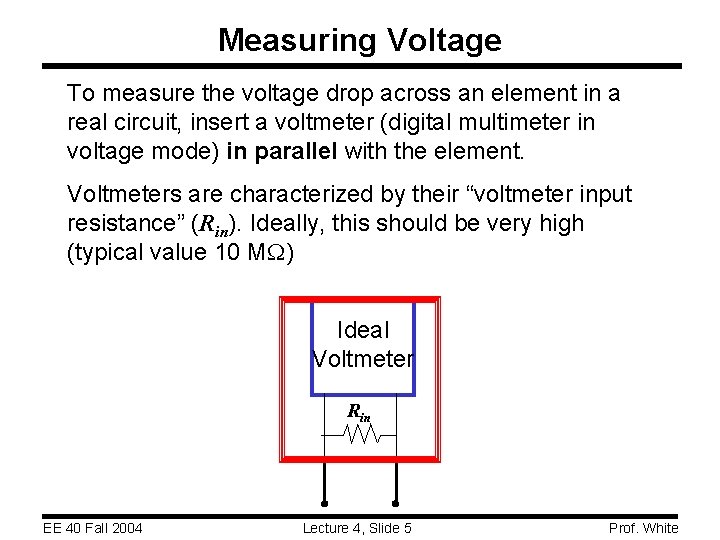
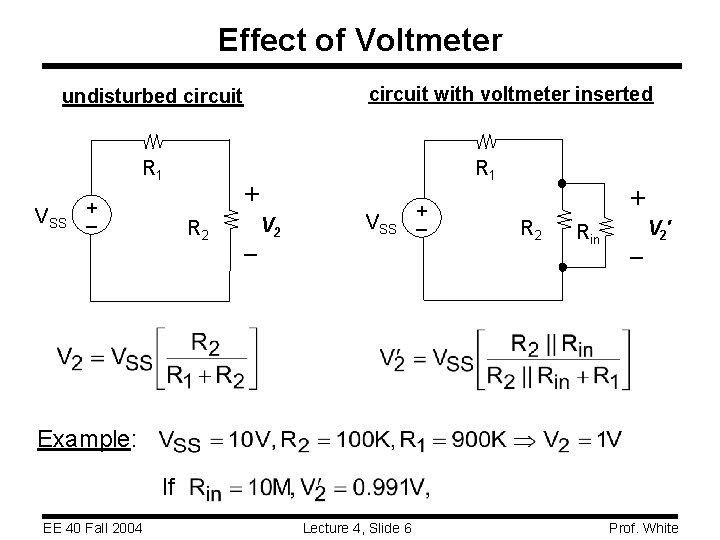
Measuring Voltage To measure the voltage drop across an element in a real circuit, insert a voltmeter (digital multimeter in voltage mode) in parallel with the element. Voltmeters are characterized by their “voltmeter input resistance” (Rin). Ideally, this should be very high (typical value 10 MW) Ideal Voltmeter Rin EE 40 Fall 2004 Lecture 4, Slide 5 Prof. White

Effect of Voltmeter circuit with voltmeter inserted undisturbed circuit R 1 VSS + _ R 1 + R 2 – V 2 VSS + _ + R 2 Rin – V 2 ′ Example: If EE 40 Fall 2004 Lecture 4, Slide 6 Prof. White

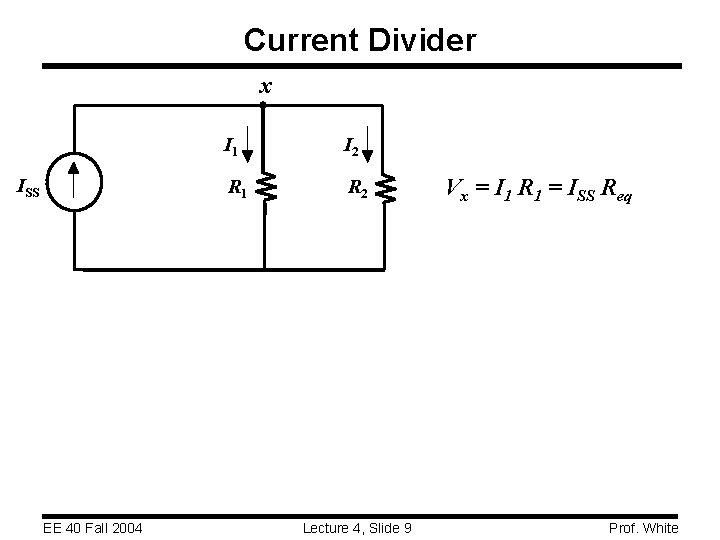
Resistors in Parallel ISS Consider a circuit with two resistors connected in parallel. Find their “equivalent resistance”. x • KVL tells us that the same voltage is dropped I 1 I 2 across each resistor Vx = I 1 R 1 = I 2 R 1 R 2 • KCL tells us EE 40 Fall 2004 Lecture 4, Slide 7 Prof. White

General Formula for Parallel Resistors What single resistance Req is equivalent to three resistors in parallel? I I + V + R 1 R 2 R 3 eq V Req Equivalent conductance of resistors in parallel is the sum EE 40 Fall 2004 Lecture 4, Slide 8 Prof. White

Current Divider x ISS EE 40 Fall 2004 I 1 I 2 R 1 R 2 Lecture 4, Slide 9 Vx = I 1 R 1 = ISS Req Prof. White

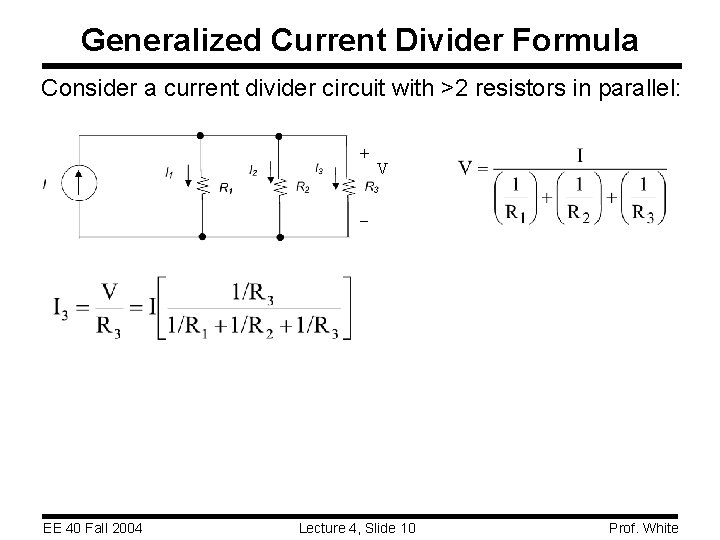
Generalized Current Divider Formula Consider a current divider circuit with >2 resistors in parallel: + V EE 40 Fall 2004 Lecture 4, Slide 10 Prof. White

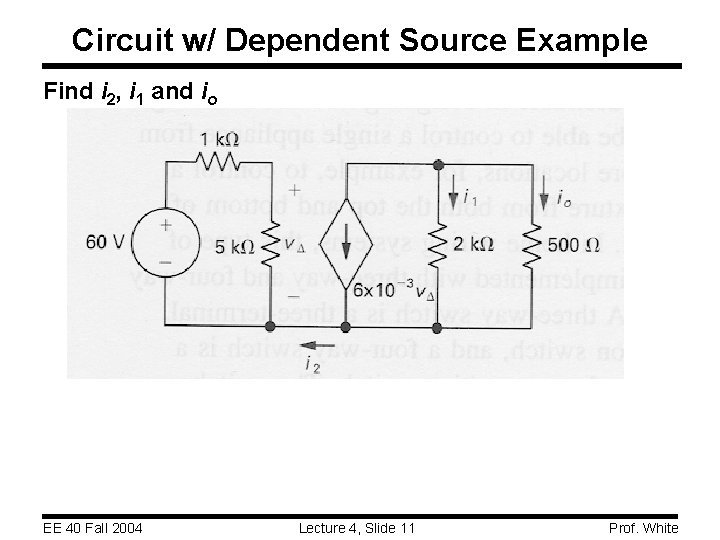
Circuit w/ Dependent Source Example Find i 2, i 1 and io EE 40 Fall 2004 Lecture 4, Slide 11 Prof. White

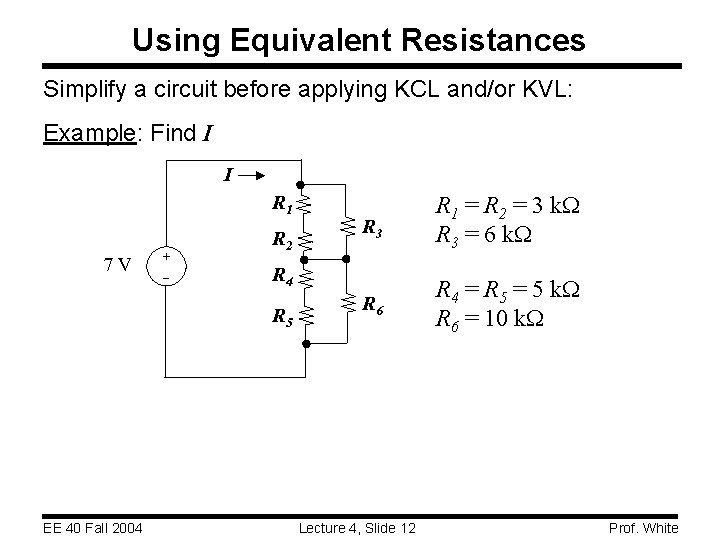
Using Equivalent Resistances Simplify a circuit before applying KCL and/or KVL: Example: Find I I R 1 7 V + R 2 R 6 R 4 = R 5 = 5 k. W R 6 = 10 k. W R 4 R 5 EE 40 Fall 2004 R 3 R 1 = R 2 = 3 k. W R 3 = 6 k. W Lecture 4, Slide 12 Prof. White

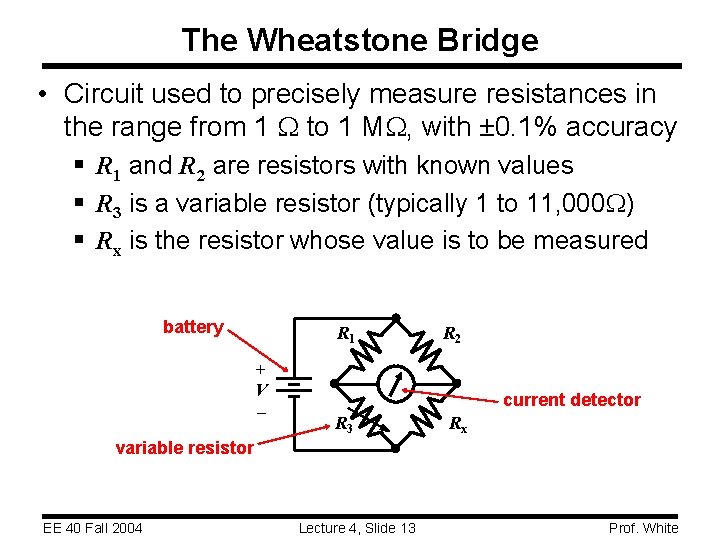
The Wheatstone Bridge • Circuit used to precisely measure resistances in the range from 1 W to 1 MW, with ± 0. 1% accuracy § R 1 and R 2 are resistors with known values § R 3 is a variable resistor (typically 1 to 11, 000 W) § Rx is the resistor whose value is to be measured battery R 1 + V – R 2 current detector R 3 Rx variable resistor EE 40 Fall 2004 Lecture 4, Slide 13 Prof. White

Finding the value of Rx • Adjust R 3 until there is no current in the detector Then, Rx = R 2 R 1 R 3 Derivation: KCL => i 1 = i 3 and i 2 = ix R 1 + V – i 1 i 2 i 3 R 2 KVL => i 3 R 3 = ix. Rx and i 1 R 1 = i 2 R 2 i 1 R 3 = i 2 Rx ix Rx R 3 Typically, R 2 / R 1 can be varied from 0. 001 to 1000 in decimal steps EE 40 Fall 2004 Lecture 4, Slide 14 R 1 = Rx R 2 Prof. White

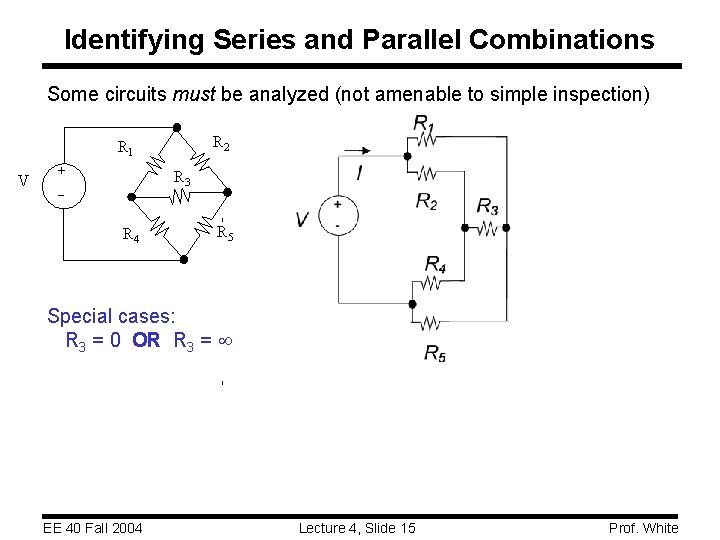
Identifying Series and Parallel Combinations Some circuits must be analyzed (not amenable to simple inspection) R 2 R 1 V + R 3 R 4 R 5 Special cases: R 3 = 0 OR R 3 = EE 40 Fall 2004 Lecture 4, Slide 15 Prof. White

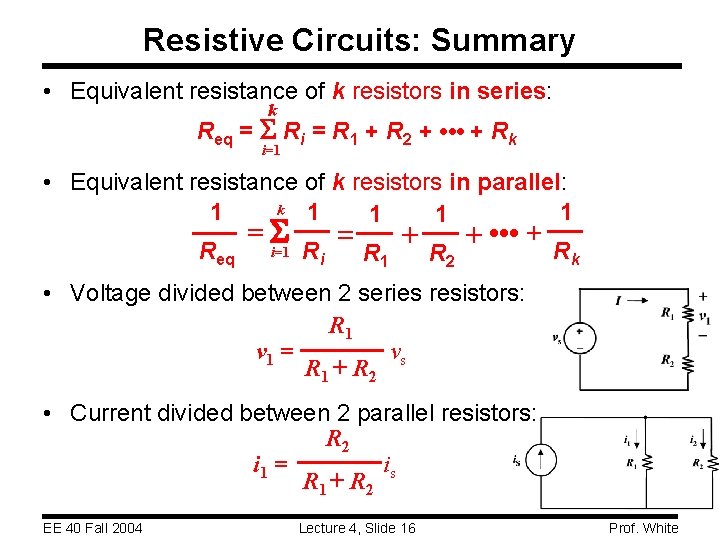
Resistive Circuits: Summary • Equivalent resistance of k resistors in series: k Req = S Ri = R 1 + R 2 + • • • + Rk i=1 • Equivalent resistance of k resistors in parallel: k 1 1 1 Req =S i=1 Ri = R 1 + R 2 + • • • + Rk • Voltage divided between 2 series resistors: R 1 v 1 = vs R 1 + R 2 • Current divided between 2 parallel resistors: R 2 i 1 = is R 1 + R 2 EE 40 Fall 2004 Lecture 4, Slide 16 Prof. White

Node-Voltage Circuit Analysis Method 1. Choose a reference node (“ground”) Look for the one with the most connections! 2. Define unknown node voltages those which are not fixed by voltage sources 3. Write KCL at each unknown node, expressing current in terms of the node voltages (using the I-V relationships of branch elements) Special cases: floating voltage sources 4. Solve the set of independent equations N equations for N unknown node voltages EE 40 Fall 2004 Lecture 4, Slide 17 Prof. White

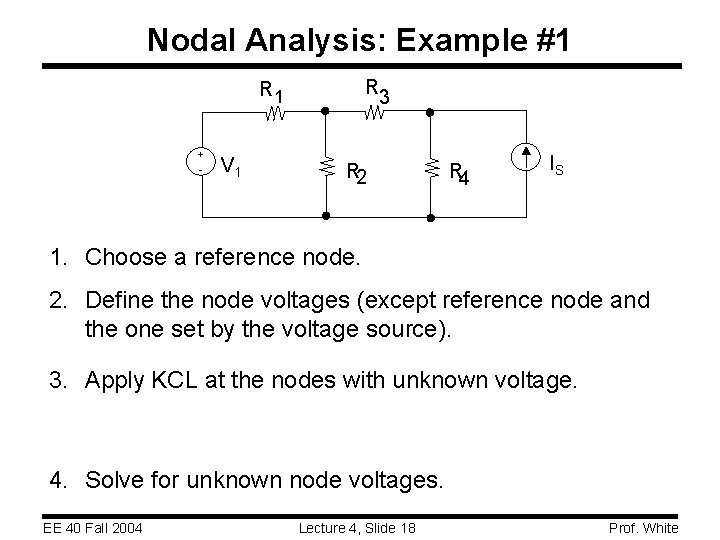
Nodal Analysis: Example #1 R 3 R 1 + - V 1 R 2 R 4 IS 1. Choose a reference node. 2. Define the node voltages (except reference node and the one set by the voltage source). 3. Apply KCL at the nodes with unknown voltage. 4. Solve for unknown node voltages. EE 40 Fall 2004 Lecture 4, Slide 18 Prof. White

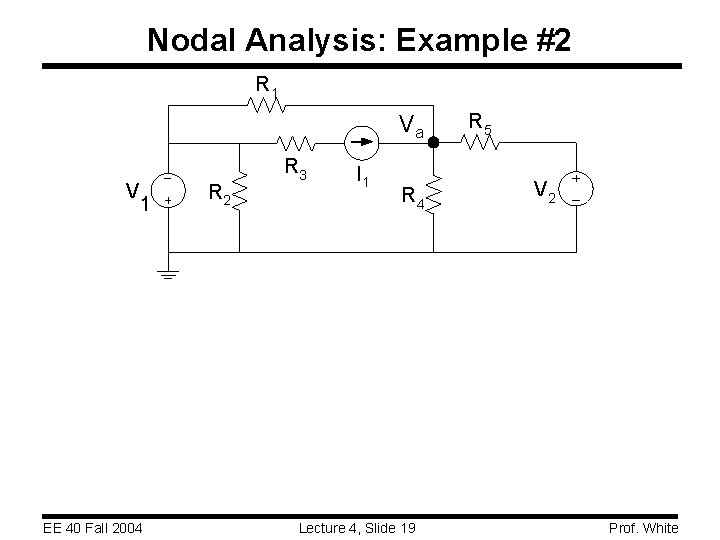
Nodal Analysis: Example #2 R 1 Va V 1 EE 40 Fall 2004 R 2 R 3 I 1 R 4 Lecture 4, Slide 19 R 5 V 2 Prof. White

Nodal Analysis w/ “Floating Voltage Source” A “floating” voltage source is one for which neither side is connected to the reference node, e. g. VLL in the circuit below: VLL Va Vb - + I 1 R 2 R 4 I 2 Problem: We cannot write KCL at nodes a or b because there is no way to express the current through the voltage source in terms of Va-Vb. Solution: Define a “supernode” – that chunk of the circuit containing nodes a and b. Express KCL for this supernode. Incorporate voltage source constraint into KCL equation. EE 40 Fall 2004 Lecture 4, Slide 20 Prof. White

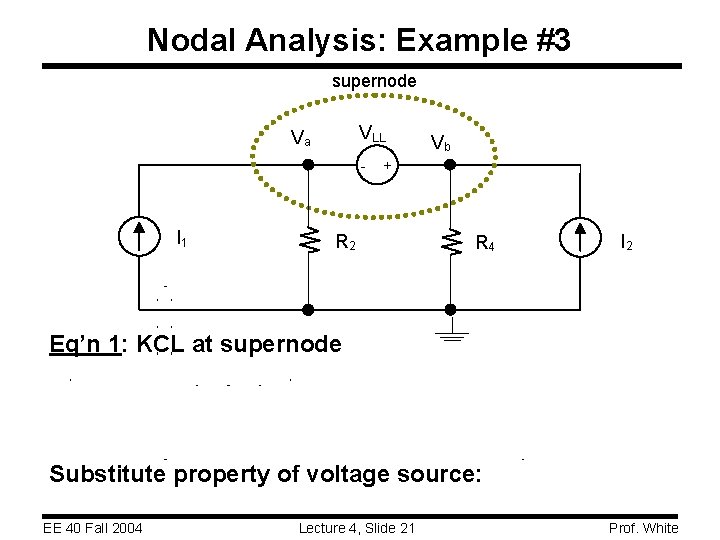
Nodal Analysis: Example #3 supernode VLL Va - I 1 Vb + R 2 R 4 I 2 Eq’n 1: KCL at supernode Substitute property of voltage source: EE 40 Fall 2004 Lecture 4, Slide 21 Prof. White