Lecture 4 Monte Carlo improvements via variance reduction

Lecture 4 - Monte Carlo improvements via variance reduction techniques: antithetic sampling n n n Antithetic variates: for any one path obtained by a gaussian variate vector draw {zi}, we generate a mirror image by changing the sign of all random numbers {zi}. Then we compute the pay-off along the two paths. The second mirrored path has the same probability of the original one. So that we can combine the two pay-offs in a new estimator: The Monte Carlo error for the improved estimate is: 5/19/2021

Monte Carlo improvements via variance reduction techniques: control variates Control variates: the Monte Carlo simulation is carried out both for the original problem as well as a similar problem for which we have a closed form solution. Being n f : the option value we want to estimate and n y : the analytical exact value of the auxiliary option an improved estimator of f is: n n As a consequence of the above relations, control variates become more and more efficient as the auxiliary option is more correlated (or anti-correlated) with the original option, i. e. when the two problems are similar. 5/19/2021

Monte Carlo improvements via variance reduction techniques: control variates and p n n Let us back to the problem of estimate p. A good choice for a control variable is a polygon with n edges inscribed in the circle. Indeed: n a closed formula exists for any value of n Stochastic term n it has an high superposition with the circle The error scales again as 1/sqrt(N) but with a smaller proportional constant : 5/19/2021

Monte Carlo improvements: low discrepancy sequences – Quasi Monte Carlo n In the standard Monte Carlo the error decreases slowly, as 1/sqrt(N), with number of samples, N, because draws do not fill in the space in a regular way. Indeed some gaps are present (clustering effects). n In low discrepancy sequences the points are chosen in order to fill in the space more regularly and uniformly, without inhomogeneities. As a result the function to be integrated converges not as one over the square root of the number of samples (N) but much more closely as one over N (Quasi Monte Carlo). 5/19/2021

Monte Carlo improvements: low discrepancy sequences – definition and results n The most famous algorithms to generate low discrepancy numbers are the Sobol and Halton sequences. n The discrepancy is a measure of how inhomogeneous a set of D-dimensional vectors of random numbers fills in a unit hypercube. n By definition, in a low discrepancy sequence (in D dimension), the discrepancy scales with the number of draws, N, as: 5/19/2021

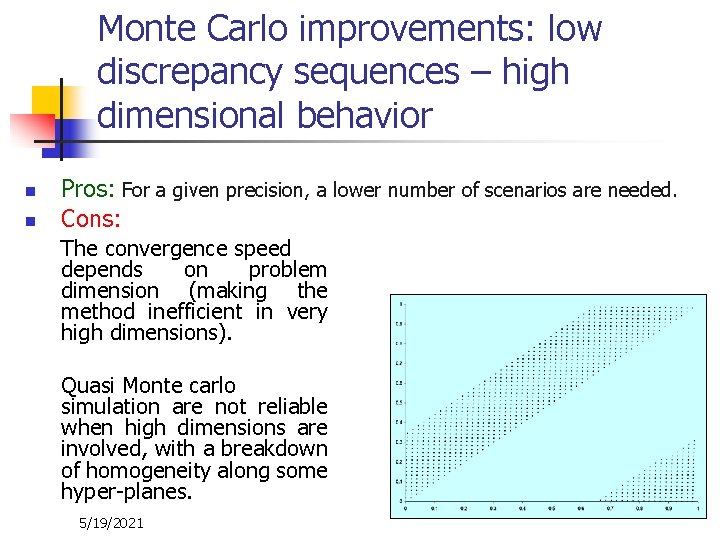
Monte Carlo improvements: low discrepancy sequences – high dimensional behavior n n Pros: For a given precision, a lower number of scenarios are needed. Cons: The convergence speed depends on problem dimension (making the method inefficient in very high dimensions). Quasi Monte carlo simulation are not reliable when high dimensions are involved, with a breakdown of homogeneity along some hyper-planes. 5/19/2021

Monte Carlo pros and cons Pros n Can be used in high dimensional problems. n Easy to implement n Easily extensible to any type of pay-off Cons: n Heavy from a computational point of view. 5/19/2021

Conclusion n We have presented a powerful numerical technique to price exotic options: the Monte Carlo method. Numerical methods in finance will become more and more important due to the rapid growth in financial markets of the exotic products, with a clear trend to increase the complexity embedded in the exotic options. References: P. Jackel - Monte Carlo Methods in Finance, Wiley Finance, (2002). 5/19/2021