Lecture 4 Models of Price Competition I Bertrand

Lecture 4: Models of Price Competition I. Bertrand (Price) Competition II. A. Homogeneous Goods III. B. Differentiated Products A. Bertrand (Price) Competition Homogeneous Products B. Assumptions: C. Homogeneous Products (Perfect Substitutes) D. No Capacity Constraints E. Timing – Consumers learn about prices instantly F. Same constant marginal cost (denoted c); no fixed costs

Di(pi) if pi<pj Di(pi, pj) = . 5 Di (pi) if pi=pj 0 if pi>pj Firms choose prices simultaneously and non-cooperatively. NE is a pair of prices pi*, pj* such that: i (pi*, pj*) i(pi, pj*) for all pi j (pi*, pj*) j(pi*, pj) for all pj Claim: pi*=c, pj*=c Result is referred to as the Bertand Paradox – It takes only two firms to obtain (perfect) competition.

B 1. Bertrand (Price) Competition: Differentiated Products Example: q 1=90 -2 p 1+p 2, q 2=90 -2 p 2+p 1, No variable costs 1= p 1 q 1 = p 1(90 -2 p 1+p 2) =90 p 1 – 2 p 12 + p 2 p 1 d 1/dp 1=90 -4 p 1+p 2 =0 or p 1=(90+p 2)/4 (Reaction function of firm 1) Similarly, p 2=(90+p 1)/4 (Reaction function of firm 2)

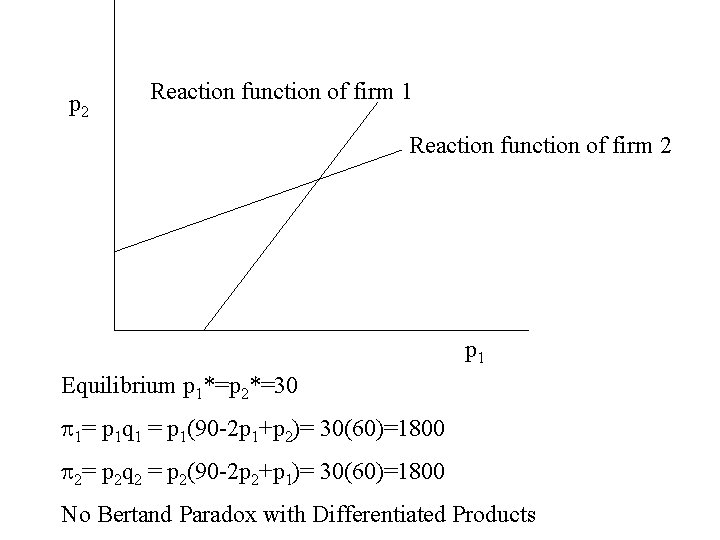
p 2 Reaction function of firm 1 Reaction function of firm 2 p 1 Equilibrium p 1*=p 2*=30 1= p 1 q 1 = p 1(90 -2 p 1+p 2)= 30(60)=1800 2= p 2 q 2 = p 2(90 -2 p 2+p 1)= 30(60)=1800 No Bertand Paradox with Differentiated Products

Comparison between Bertrand Cournot Competition: Example: q 1=90 -2 p 1+p 2, q 2=90 -2 p 2+p 1 Bertrand Competition: p 1*=p 2*=30, q 1*=q 2*=60, 1 = 2 = 1800 Cournot Competition: Derive (inverse) demand curves: p 1=(270 -2 q 1 -q 2)/3, p 2=(270 -2 q 2 -q 1)/3 1= p 1 q 1 = (270 -2 q 1 -q 2)q 1/3. FOC: 270 -4 q 1 -q 2=0. q 1*=q 2*=54, p 1*=p 2*=36, 1 = 2 =1944

Intuitively Explaining the Results Under Bertrand Competition, the elasticity of demand is e(B)=-(P/Q) (d. Q/d. P) = 2 P/Q e(C)=-(P/Q) (d. Q/d. P) = 1. 5 P/Q Perceived Elasticity of Demand Lower Under Cournot Competition. (True for all linear demand curves. ) Hence, profits are higher under Cournot competition.

B 2: Price Competition with Differentiated Products: Hotelling (1929) Model B A 0 1 City of length one (1) unit Two firms: denoted A & B at different ends of the interval Consumers uniformly distributed on [0, 1]. (Another interpretation is that consumer tastes are uniformly distributed on the interval) Unit Cost is “c” Transportation cost of “k” per unit distance (x) Consumers have unit demands, i. e. , they purchase one unit of good Except for distance, goods are homogenous with gross utility “v. ”

B A 0 x 1 A consumer located at “x” incurs a transportation cost of “kx” to purchase from firm A, and a transportation cost of “k(1 -x)” to purchase from firm B. Net utility: U(A)=v-p. A-kx (where price p. A is charged by firm A) Net utility: U(B)=v-p. B-k(1 -x) (where price p. B is charged by firm B) Under the assumption that prices are not too high relative to “v, ” the market is fully covered. In such a case, marginal consumer (x) is indifferent between the two good, i. e. , U(A)=U(B). Marginal consumer x=(p. B – p. A + k)/2 k.

Demand for good A, DA(p. A, p. B)= x= (p. B – p. A + k)/2 k. Demand for good B, DB(p. A, p. B)= (1 -x) =(p. A – p. B + k)/2 k. Hence: A= (p. A-c) DA(p. A, p. B)= (p. A-c)(p. B – p. A + k)/2 k. B= (p. B-c) DB(p. A, p. B)= (p. B-c)(p. A – p. B + k)/2 k. FOC: - (p. A-c) + (p. B – p. A + k) = 0 - (p. B-c) + (p. A – p. B + k) = 0 p. A=(p. B + c + k)/2. (firm A) p. B=(p. A + c + k)/2. (firm B) Nash equilibrium prices: p. A*=p. B*= c+k. Equilibrium profits: A*= B*= k/2. When the products are more differentiated (larger k), prices are higher. When k 0, the model approaches Bertrand competition with homogeneous products.

Different Locations along line: • We looked at the case of maximum differentiation. • When the products are in the same location, competition will force the price down to marginal cost (p. A*=p. B*= c). • Different Locations (but not at the end of the line) - need quadratic transportation costs to insure equilibrium: Example PS 2, #4 0 A B 4 8 x 9 4 -x U(A)=v-p. A-2 x 2 , U(B)=v-p. B-2(4 -x)2 A= (p. A-c) (4+x) , B= (p. B-c) [1+(4 -x)] x=(p. B-p. A+32)/16