Lecture 4 Interference and diffraction of light I

Lecture 4: Interference and diffraction of light (I) Young’s two slit experiment (Y&F 35. 2) o To observe interference of light one needs to set-up two independent, coherent, monochromatic (same frequency) light sources. o Coherent light sources are difficult to make since light is emitted by the random agitation of atoms (we will see later on that lasers can be sources of coherent light). S 1 S 0 S 2 o To achieve two coherent sources of light, we can use a common source and split it such that the light emerges from two secondary sources, so the relative phase between them is always the same. P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 1

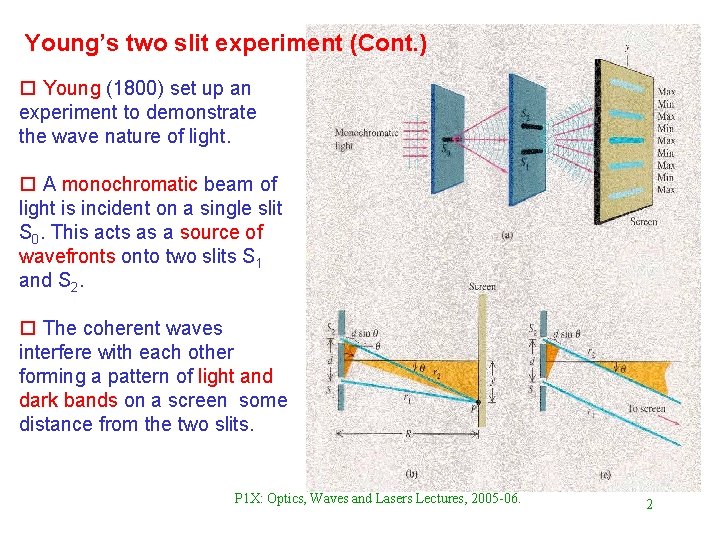
Young’s two slit experiment (Cont. ) o Young (1800) set up an experiment to demonstrate the wave nature of light. o A monochromatic beam of light is incident on a single slit S 0. This acts as a source of wavefronts onto two slits S 1 and S 2. o The coherent waves interfere with each other forming a pattern of light and dark bands on a screen some distance from the two slits. P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 2

Geometry of Young’s two slit experiment o The triangle S 1 S 2 Q means that: S 1 Q = d sin q o. If the screen is at a distance R which is much larger than the separation d of the two slits (R could be a few metres and d a few millimetres) then r 1 and r 2 are nearly parallel to each other and q is small: d sin q = r 2 - r 1 S 1 Q d Intensity q S 2 q q r 2 y r 1 P R P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 3

o Constructive interference: bright fringes o. Destructive interference: dark fringes P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 4

o Example 35 -1 (Y&F): In a two slit interference experiment, the slits are 0. 20 mm apart, and the screen at a distance of 1. 0 m. The third bright fringe (not counting the central bright fringe) is displaced by 7. 5 mm. Find the wavelength of light used. Third fringe: m=3, R=1. 0 m, d=0. 2 mm, R>>d Another possibility: m= -3 ym= -7. 5 mm P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 5

o Example L 61 (Example book): Light from a source containing 2 wavelengths of 567 nm and 486 nm illuminates a double slit arrangement with d=1. 0 mm and R=1. 50 m. At what distance from the central fringe on the screen will a bright fringe from one interference pattern coincide with the bright fringe from the other interference pattern. Bright fringes: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 6

Intensity in interference patterns (Y&F, 35. 3) o The waves associated with light are called electromagnetic waves. Unlike the other waves we have encountered, they don’t need a medium to propagate. They can propagate in vacuum. o In the two slit experiment we have an electric field coming from S 1: and another coming from S 2: (frequency and amplitude are the same since the two sources are coherent). Principle of superposition: P. 1463 Y&F Trigonometric functions Since: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 7

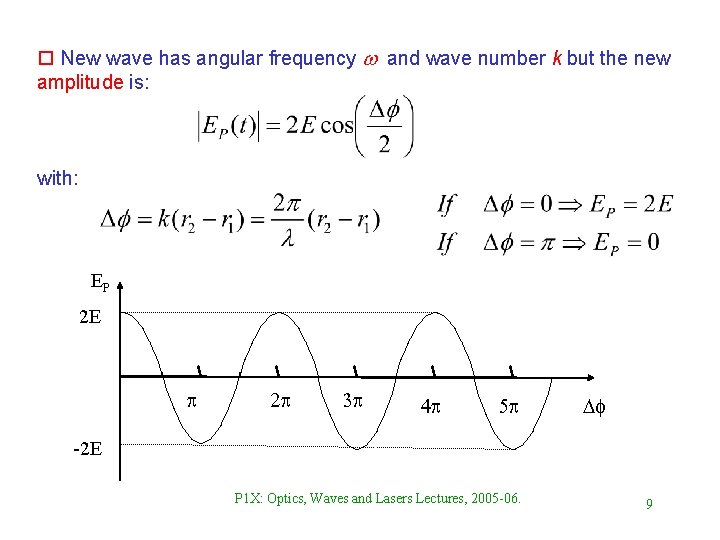
o Since: Then: o Phase difference between two waves: r 2 -r 1 is called the path difference. o New wave: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 8

o New wave has angular frequency w and wave number k but the new amplitude is: with: EP 2 E p 2 p 3 p 4 p 5 p Df -2 E P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 9

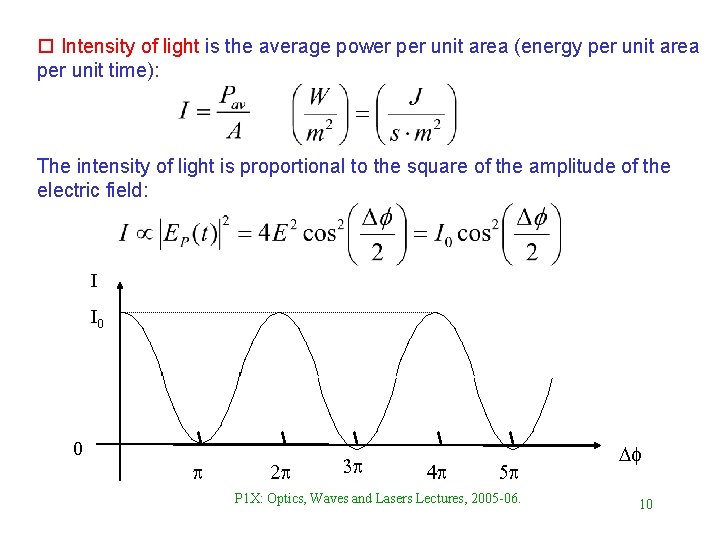
o Intensity of light is the average power per unit area (energy per unit area per unit time): The intensity of light is proportional to the square of the amplitude of the electric field: I I 0 0 p 2 p 3 p 4 p 5 p P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. Df 10

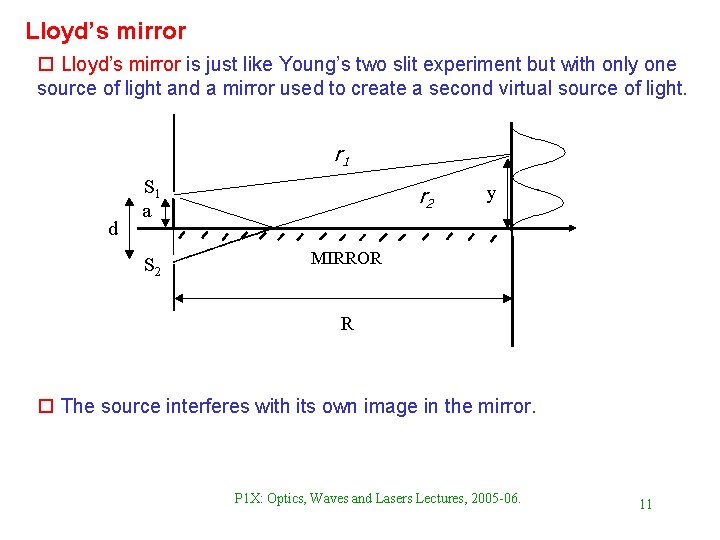
Lloyd’s mirror o Lloyd’s mirror is just like Young’s two slit experiment but with only one source of light and a mirror used to create a second virtual source of light. r d S 1 a S 2 r 1 r 2 y y r 2 I MIRROR R o The source interferes with its own image in the mirror. P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 11

o There is a phase change of p radians due to the reflection of the mirror (equivalent to a path difference of l/2). EP EP p Df 2 p BEFORE MIRROR p 2 p Df AFTER MIRROR o The constructive and destructive conditions are reversed with respect to Young’s experiment and there is a dark fringe next to the mirror. • Constructive interference: bright fringes • Destructive interference: dark fringes P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 12