Lecture 4 From Extensive to Strategic Form This

Lecture 4 From Extensive to Strategic Form This lecture shows how to derive the strategic form from the extensive form, and illustrates their equivalence in simultaneous move games. Key words and phrases: players, actions, information, payoffs, strategies, strategic profiles, expected payoffs.

The strategic versus the extensive form In the first lecture we defined a game using its strategic form. It has three elements: 1. Players 2. Strategies 3. Expected payoffs. Then in the third lecture we defined a game using its extensive form. It has four elements: 1. 2. 3. 4. Players. . Who is involved? Moves. . What can they do at different points? Information. . How much do they know when they move? Payoffs. . How do they value the outcomes? These are two ways of representing the same game.

Analyzing strategic interactions begins with the extensive form The extensive form is a more comprehensive way of representing a game than the strategic form. There are many examples of games with different extensive forms that have the same strategic form (but not the other way around). To study strategic interactions, it is therefore more useful to start with the extensive form of a game rather than the strategic form.

But for solving games? Sometimes it easier to solve the game in its strategic form; at other times solving the extensive form is easier. The cola wars case study already hinted at that: 1. in the simultaneous move game it seemed easier to solve the game when presented in its strategic form. 2. when Coke could observe Pepsi’s move before making its own choice (in what is called a perfect information game), solving the game in its extensive form looked straightforward. Note that NE are defined with respect to the strategic form, not the extensive form. So to find the NE for a game defined in its extensive form, we must first derive the strategic form from the extensive form.

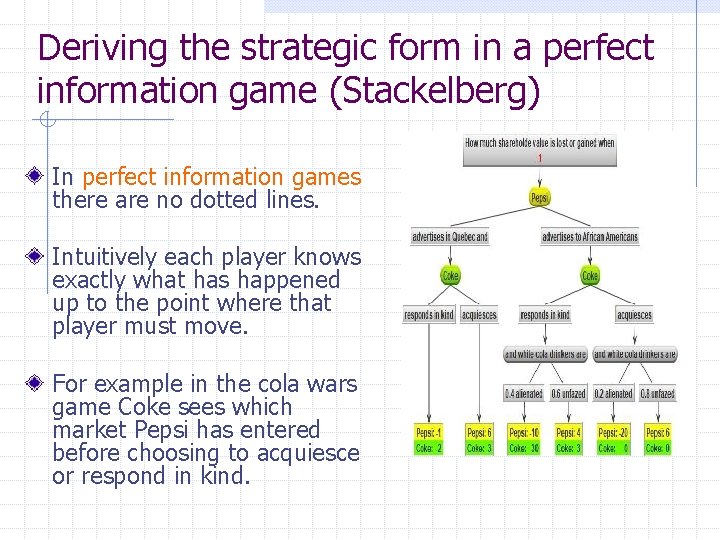
Deriving the strategic form in a perfect information game (Stackelberg) In perfect information games there are no dotted lines. Intuitively each player knows exactly what has happened up to the point where that player must move. For example in the cola wars game Coke sees which market Pepsi has entered before choosing to acquiesce or respond in kind.

The Strategy Space for Pepsi What happens if we try to solve the game with its strategic form? Pepsi is a first mover, and makes no further moves in the game. Furthermore nature (consumer demand tastes) follow Pepsi’s move. That is Pepsi moves without knowing nature’s moves. Therefore each of Pepsi’s two moves corresponds to precisely one strategy: 1. 2. Advertise in Quebec. Advertise to African Americans.

The Strategy Space for Coke, like Pepsi, only makes one move in this game. However Coke moves second, and can see the move Pepsi has taken before it makes its own. Therefore Coke can condition on what Pepsi does in formulating its own strategy. Thus Coke has four strategies: 1. 2. 3. 4. Always acquiesce. Always respond in kind. Acquiesce if Pepsi advertises in Quebec and respond in kind if Pepsi advertises to African Americans. Acquiesce if Pepsi advertises to African Americans and respond in kind if Pepsi advertises in Quebec.

Matching strategy pairs to expected payoffs For each strategy pair we calculate the expected payoff to both of the players. First, suppose Pepsi advertises in Quebec and Coke always acquiesces. That is they both choose their first strategy. Then the payoff to: 1. 2. Pepsi is 6 Coke is -3 Second, suppose Pepsi advertises to African Americans and Coke always acquiesces. Then the expected payoff to: 1. 2. Pepsi is 6*0. 8 - 20*0. 2 = 4. 8 – 4 = 0. 8 Coke is 0*0. 8 - 0*0. 2 = 0

The Strategic Form Illustrated The bi-matrix is created by forming rows from Pepsi’s strategies, columns from Coke’s strategies and filling in the expected payoffs in the cell corresponding to each strategy pair.

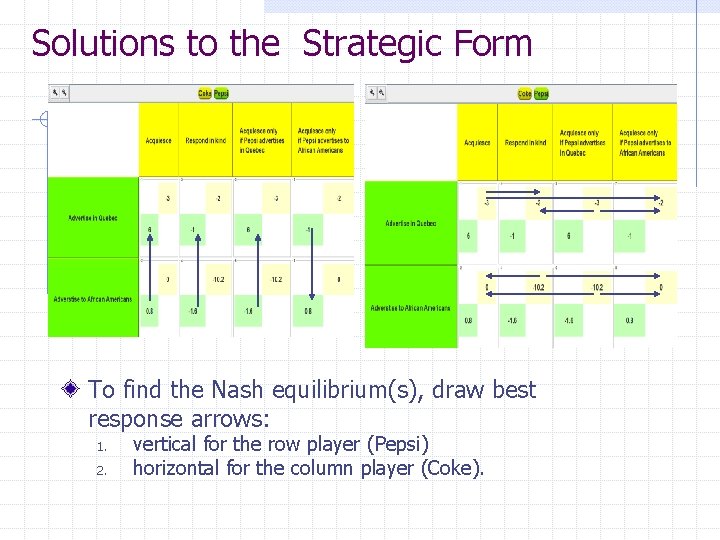
Solutions to the Strategic Form To find the Nash equilibrium(s), draw best response arrows: 1. 2. vertical for the row player (Pepsi) horizontal for the column player (Coke).

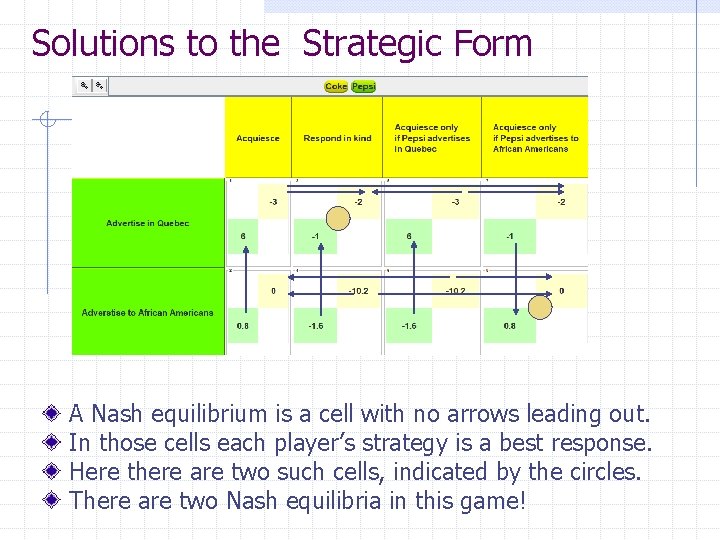
Solutions to the Strategic Form A Nash equilibrium is a cell with no arrows leading out. In those cells each player’s strategy is a best response. Here there are two such cells, indicated by the circles. There are two Nash equilibria in this game!

One of the Nash equilibrium is implausible Suppose Pepsi “advertises to African Americans”. Why would Coke “respond in kind”? This is implausible. For if Coke plays the far right strategy, it cannot lose! For this reason Coke’s fourth strategy is called a (weakly) dominant strategy. The plausible Nash equilibrium is called subgame perfect and exactly corresponds to the solution found by applying backwards induction to the extensive form!

Comparing the solutions of the strategic and extensive forms Coke playing the far right strategy, acquiescing only if Pepsi advertises to African Americans (the fourth strategy), guarantees itself the highest payoff regardless of what Pepsi does. For this reason Coke’s fourth strategy is called a (weakly) dominant strategy. If Coke plays this strategy, then the best strategy of Pepsi is to advertise to African Americans. The plausible Nash equilibrium is called subgame perfect and exactly corresponds to the solution we found by applying the backwards induction to the extensive form!

The strategies for Pepsi and Coke in this simultaneous move game As in the perfect information game Pepsi has just two strategies: 1. Advertise in Quebec. 2. Advertise to African Americans. In contrast to the perfect information game Coke cannot condition on what Pepsi has done in this game. It is as if they moved simultaneously: hence the name. Thus Coke also only has two strategies: 1. Respond in kind. 2. Acquiesce.

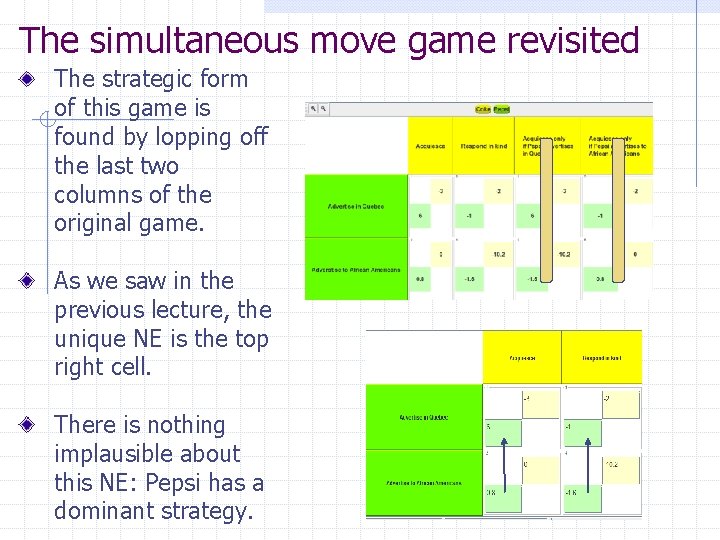
The simultaneous move game revisited The strategic form of this game is found by lopping off the last two columns of the original game. As we saw in the previous lecture, the unique NE is the top right cell. There is nothing implausible about this NE: Pepsi has a dominant strategy.

Deriving the strategic form of a game from its extensive form The cola wars case study shows it is useful to know how to solve games using both the strategic and extensive forms. There are essentially three steps to deriving the strategic form from the extensive form: 1. List all the (pure) strategies for every player. 2. Using the first step list all the strategy profiles (a strategy for each player) formed from all possible permutations of the strategies. 3. For each strategy profile compute the expected payoff for every player. In the second step, if for example, player n =1, 2, 3 has n+1 strategies in a 3 player game, then there are: 2*3*4 = 24 strategy profiles.

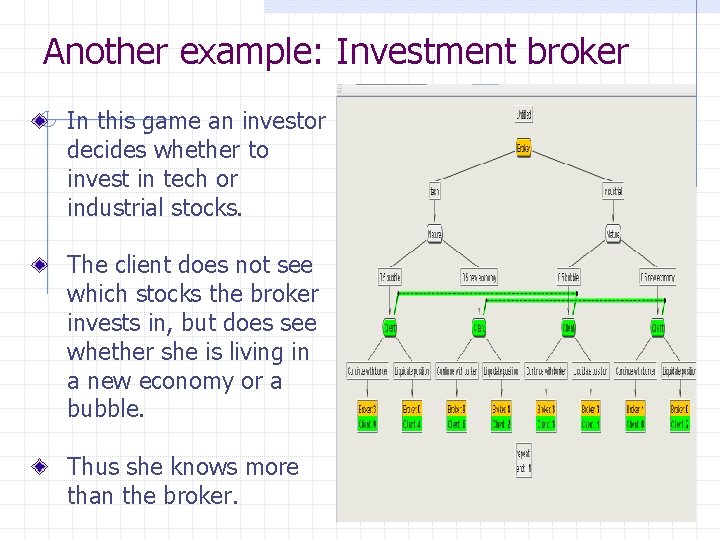
Another example: Investment broker In this game an investor decides whether to invest in tech or industrial stocks. The client does not see which stocks the broker invests in, but does see whether she is living in a new economy or a bubble. Thus she knows more than the broker.

Strategies for both players The broker has two strategies: 1. Tech. 2. Industrial. The client however has four strategies: 1. Always continue with broker. 2. Always liquidate. 3. Continue with broker if she is living in a bubble and liquidate if she is living in a new economy. 4. Continue with broker if she is living in a new economy and liquidate if she is living in a bubble.

Computing the expected payoffs for the strategy profiles Consider the following strategy pair: 1. The broker chooses “tech” 2. The client chooses “Continue with broker if she is living in a bubble and liquidate if she is living in a new economy. What is the expected payoffs to each player? From the game tree we see that the: 1. broker gets 0. 5(3 + 4) = 3. 5. 2. client gets 0. 5(-9 + 2) = -3. 5. The expected payoffs for the other strategy pairs are calculated in exactly the same way.

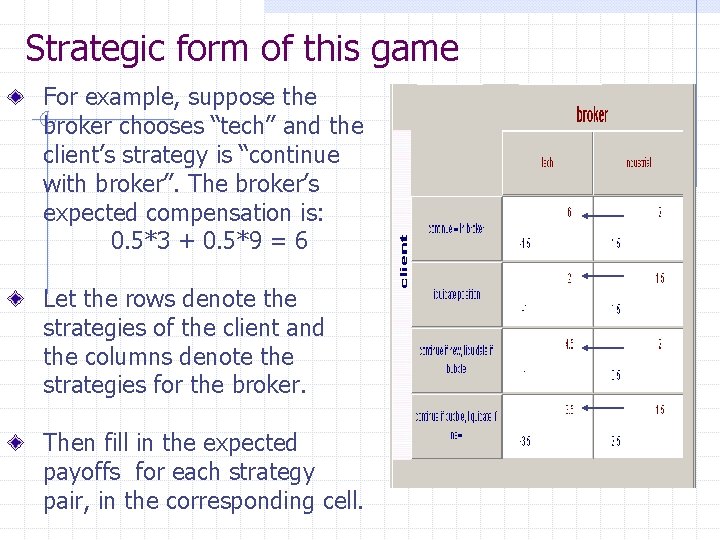
Strategic form of this game For example, suppose the broker chooses “tech” and the client’s strategy is “continue with broker”. The broker’s expected compensation is: 0. 5*3 + 0. 5*9 = 6 Let the rows denote the strategies of the client and the columns denote the strategies for the broker. Then fill in the expected payoffs for each strategy pair, in the corresponding cell.

Solution to investment broker The broker should choose “tech” because regardless of which strategy “Tech is an example of a dominant strategy. If the investor recognized that the broker had a dominant strategy, the investor would use the signal she receives about the economy, picking the strategy “continue if new, liquidate if bubble”. In that case she would be using the principle of iterated dominance to solve the game.