Lecture 4 Dynamics Newtons Laws of Motion l

Lecture 4 Dynamics: Newtons Laws of Motion l Objects undergo motion and accelerations. This is caused by an interaction between bodies. Such interactions are called forces. Recall most of our forces are contact forces l Newton’s laws of motion: Published Newton’s Principia (1642) 1

NEWTON’S FIRST LAW An object continues in a state of rest or of motion at constant speed in a straight line unless acted upon by a net force. If you push it and let it go, it will move at constant velocity. Example : Hockey puck of mass m on ice Block of Ice 2

l Examples of Contact Forces: çA push or pull can be a force çNormal force çTension in a string ç Friction çTwo balls colliding. l Example of Noncontact forces çGravitation çElectric

NEWTON’S FIRST LAW An object continues in a state of rest or of motion at constant speed in a straight line unless acted upon by a net force. If you don’t push it, it won’t move. A body has inertia. Example : Hockey puck of mass m on ice Block of Ice 4

Inertia Another way of understanding the First Law Inertia is a bodies resistance to change due to forces. Inertia is related to mass. Some examples of inertia • Hit a nail in a piece of wood on an anvil sitting on your head • Mass on string (Demo) 5

Two different ways of breaking the string: Inertia and Tension Upper string breaks when you pull slowly because tension is greater Lower string breaks when you pull quickly because of inertia First pull fast see where it breaks Then pull slowly see where it breaks Explain 6

NEWTON’S SECOND LAW = sum of all external forces acting on the body = net force System SI CGS BE Mass kg g slug (sl) Acceleration m/s 2 cm/s 2 ft/s 2 Force Newton (N) dyne (dyn) pound (lb) 7

Now let’s combine Newton’s Second Law F=ma and his Law of Gravitation to find the acceleration of gravity g. Where does the value of g come from? 8

Newton’s Universal Law of Gravitation Mass m at height h h R Earth has mass M 9

Where does the value of g come from? Mass m at height h h R Earth has mass M 10

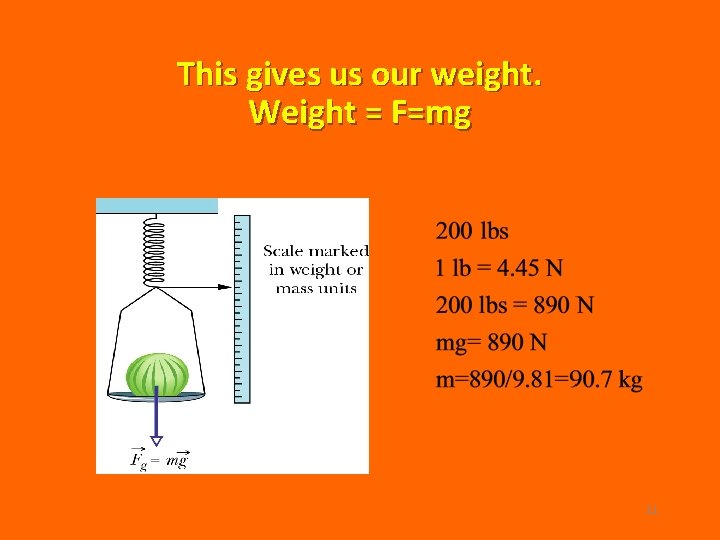
This gives us our weight. Weight = F=mg 11

At the equator the earths effective g is 9. 7805 m/s 2. The acceleration at the equator due to the earths rotation is 0. 0339 m/s 2. This means that the true gravitational acceleration is 9. 8144=9. 7805+0. 0339 m/s 2 At the poles the Gravitational acceleration is 9. 8322 m/s 2 The difference between the poles and the equator is that objects on the Equator are still about 21 km away from the center of the earth. In summary the difference between the poles and the equator is 70% is due to the acceleration and 30% is due to the oblateness 12

NEWTON’S THIRD LAW When two bodies interact, the forces on the bodies due to each other are always equal in magnitude and opposite in direction. M Gravitational Interaction E 13

NEWTON’S THIRD LAW When two bodies interact, the forces on the bodies due to each other are always equal in magnitude and opposite in direction. M T Contact Interaction E 14

Rules for drawing free body diagrams. Isolates the forces acting on one body • Represent the body by a point. • Each force acting on the body is represented by a vector with tail at the point and the length of vector indicating the approximate magnitude of the force. • If the situation consist of several bodies which are rigidly connected, you can still represent all the bodies by a point and use the total mass. Internal 15 forces are not included.

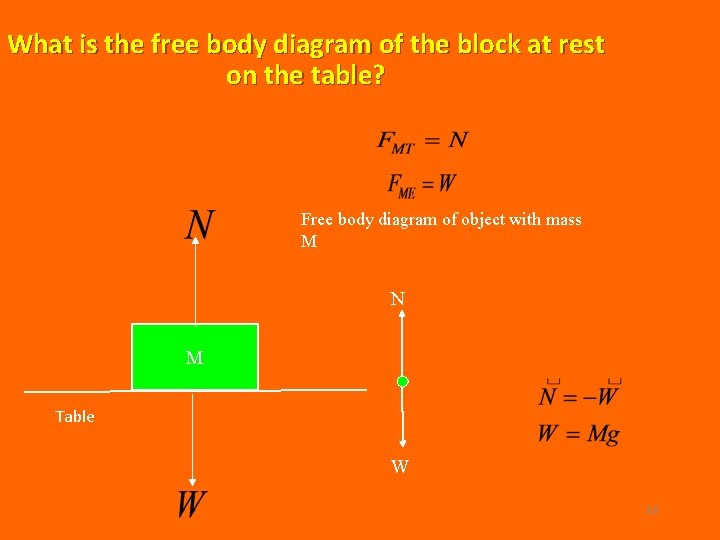
What is the free body diagram of the block at rest on the table? Free body diagram of object with mass M N M Table W 16

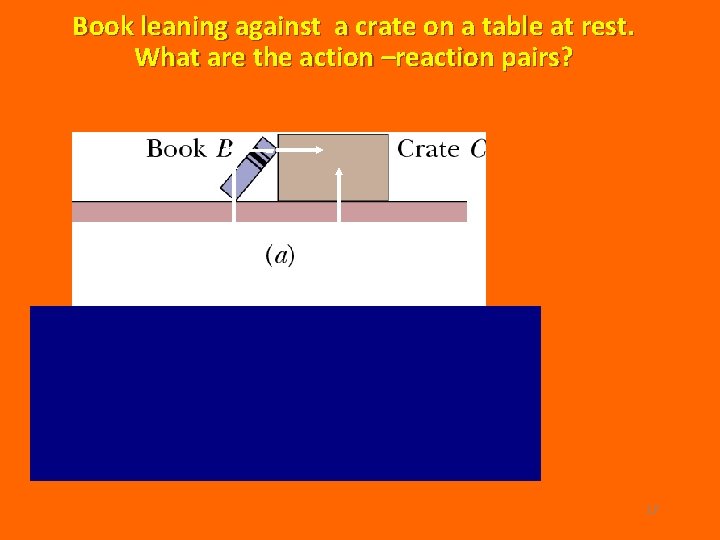
Book leaning against a crate on a table at rest. What are the action –reaction pairs? Table T 17

1) Draw a free body diagram of the forces acting on the crate NT B mg 18

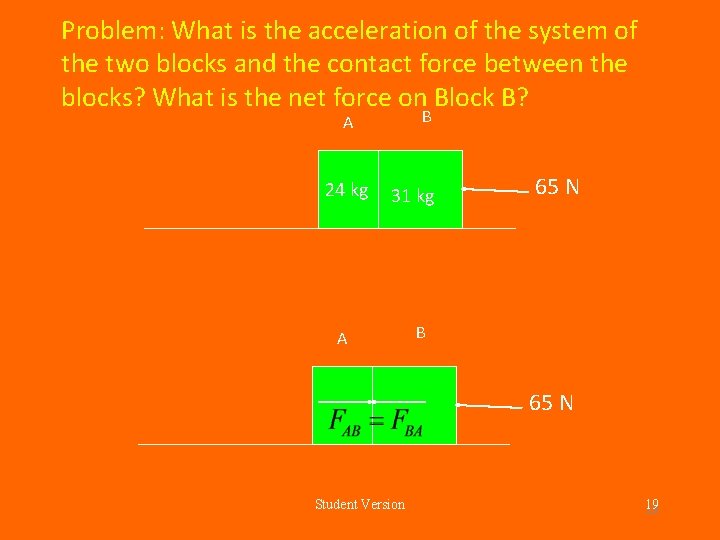
Problem: What is the acceleration of the system of the two blocks and the contact force between the blocks? What is the net force on Block B? B A 24 kg 31 kg A 65 N B 65 N Student Version 19 19

Problem: What is the acceleration of the system of the two blocks and the contact force between the blocks? What is the net force on Block B? B A 24 kg 31 kg A 65 N B 65 N Student Version 20 20

Now lets look at tension in a string Tension in the string is equal to the weight = 10 N The scale reads the tension in the string 21

Is the tension in the string any different when I have weights pulling it down on both sides? 10 N 10 N 22

Problem 1212 kg kg 24 24 kg kg 31 kg T 3=65 N kg 65 N a) What is the acceleration of the system? b) Find T 1 c) Find T 2 a) b) c) 23

A crate is being pulled by a man as shown in the figure. What is the acceleration of the crate along the x direction? Man does not move. +y N T f +x m= 310 kg W x component of forces in free body diagram 24

What is the normal force assuming there is no acceleration in the y direction? N T f W y component of forces in free body diagram 25

Rev George Atwood’s machine 1746 -1807 Tutor Trinity College, Cambridge 1 2 26

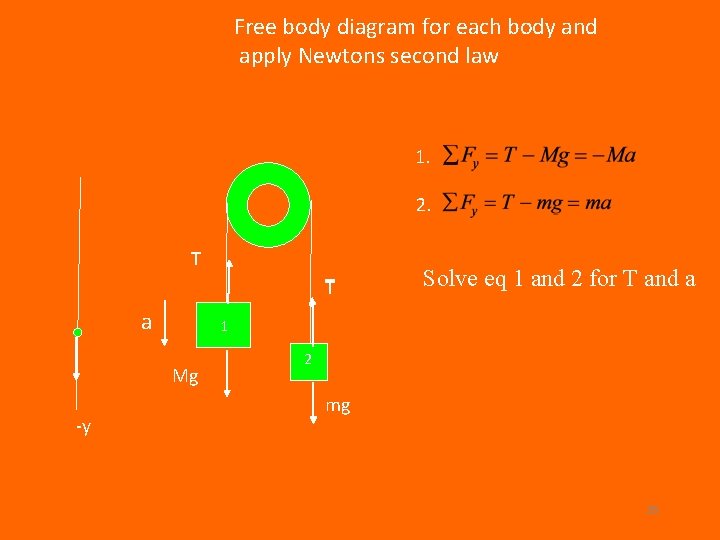
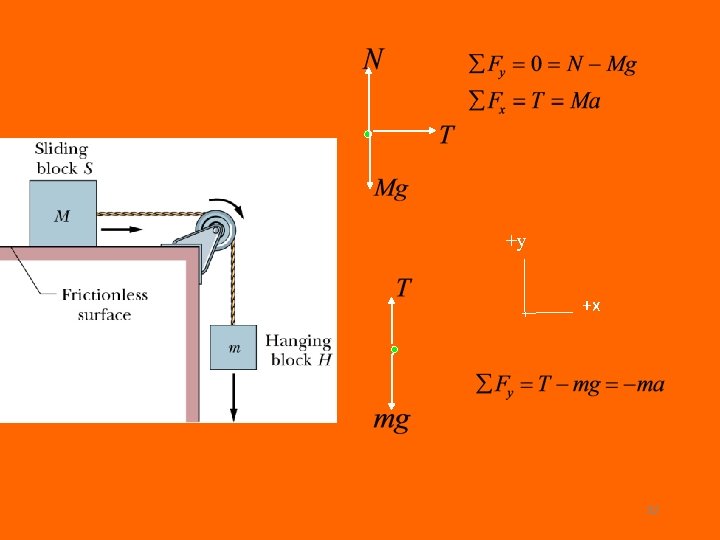
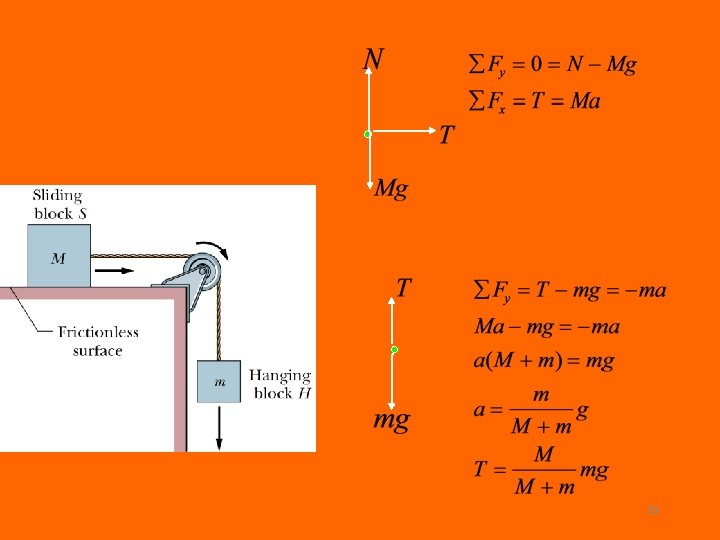
1) 2) 3) 4) Set up Coordinate system Assume acceleration in some direction Draw free body diagram for each body Apply Newtons second law to each body 1) Take negative y direction as down 2) Assume mass 1 is going down T T a 1 Mg -y 2 mg 27

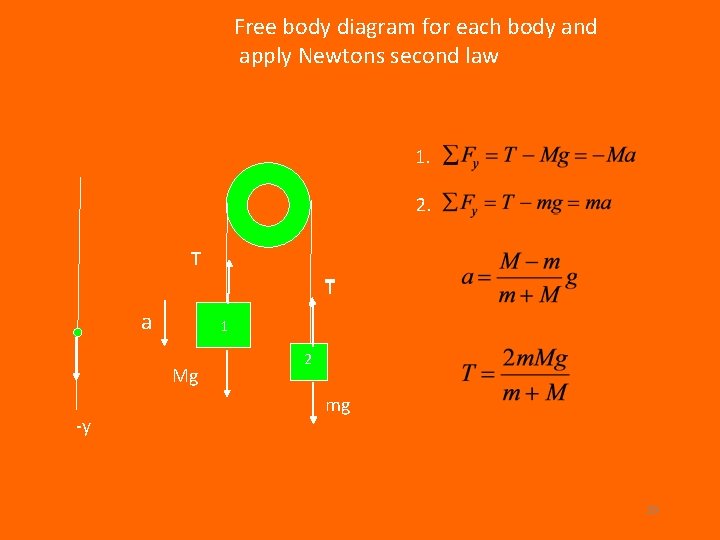
Free body diagram for each body and apply Newtons second law 1. 2. T T a 1 Mg -y Solve eq 1 and 2 for T and a 2 mg 28

Free body diagram for each body and apply Newtons second law 1. 2. T T a 1 Mg -y 2 mg 29

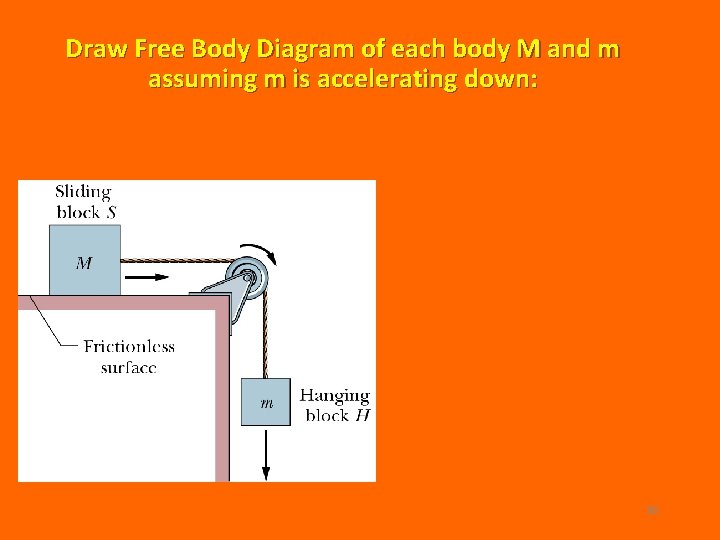
Draw Free Body Diagram of each body M and m assuming m is accelerating down: Frictionless pulley T T 30

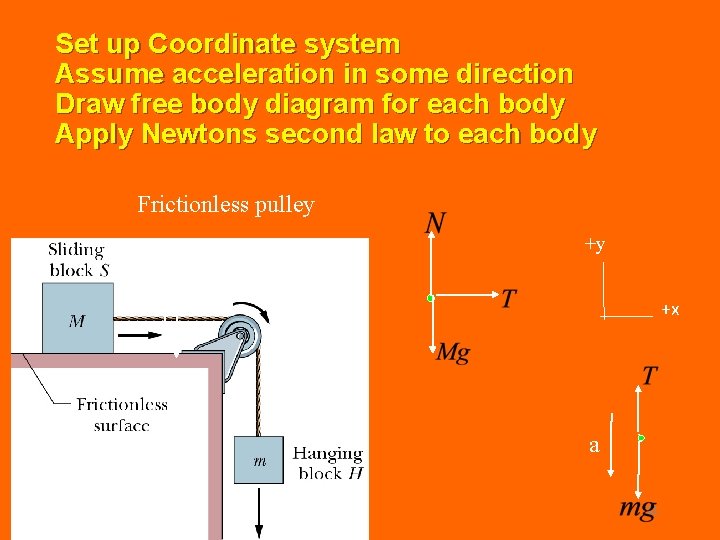
Set up Coordinate system Assume acceleration in some direction Draw free body diagram for each body Apply Newtons second law to each body Frictionless pulley +y +x T a 31

+y +x 32

33

Tug-of-war demo illustrates how a small sideways force can produce a large horizontal force Suppose two guys in the tug of war are at 4. 5 meters apart and I pull the rope out 0. 15 meters. Then φ =4 degrees 2. 25 m Therefore, f If then The smaller the angle the larger the magnification

Concep. Test 4. 1 a Newton’s First Law I A book is lying at rest on a table. The book will remain there at rest because: 1) there is a net force but the book has too much inertia 2) there are no forces acting on it at all 3) it does move, but too slowly to be seen 4) there is no net force on the book 5) there is a net force, but the book is too heavy to move

Concep. Test 4. 1 a Newton’s First Law I A book is lying at rest on a table. The book will remain there at rest because: 1) there is a net force but the book has too much inertia 2) there are no forces acting on it at all 3) it does move, but too slowly to be seen 4) there is no net force on the book 5) there is a net force, but the book is too heavy to move There are forces acting on the book, book but the only forces acting are in the y-direction. Gravity acts downward, but the table exerts an upward force that is equally strong, so the two forces cancel, leaving no net force

Concep. Test 4. 1 b Newton’s First Law II A hockey puck slides on ice at constant velocity. What is the net force acting on the puck? 1) more than its weight 2) equal to its weight 3) less than its weight but more than zero 4) depends on the speed of the puck 5) zero

Concep. Test 4. 1 b Newton’s First Law II A hockey puck slides on ice at constant velocity. What is the net force acting on the puck? 1) more than its weight 2) equal to its weight 3) less than its weight but more than zero 4) depends on the speed of the puck 5) zero The puck is moving at a constant velocity, velocity and therefore it is not accelerating Thus, there must be no net force acting on the puck. Follow-up: Are there any forces acting on the puck? What are they?

Concep. Test 4. 1 c Newton’s First Law III You put your book on the bus seat next to you. When the bus stops 1) a net force acted on it 2) no net force acted on it suddenly, the book 3) it remained at rest slides forward off the 4) it did not move, but only seemed to seat. Why? 5) gravity briefly stopped acting on it

Concep. Test 4. 1 c Newton’s First Law III You put your book on the bus seat next to you. When the bus stops 1) a net force acted on it 2) no net force acted on it suddenly, the book 3) it remained at rest slides forward off the 4) it did not move, but only seemed to seat. Why? 5) gravity briefly stopped acting on it The book was initially moving forward (since it was on a moving bus). When the bus stopped, the book continued moving forward, forward which was its initial state of motion, motion and therefore it slid forward off the seat. Follow-up: What is the force that usually keeps the book on the seat?

Concep. Test 4. 1 d Newton’s First Law IV You kick a smooth flat stone out on a frozen pond. The stone slides, slows down and eventually stops. You conclude that: 1) the force pushing the stone forward finally stopped pushing on it 2) no net force acted on the stone 3) a net force acted on it all along 4) the stone simply “ran out of steam” 5) the stone has a natural tendency to be at rest

Concep. Test 4. 1 d Newton’s First Law IV You kick a smooth flat stone out on a frozen pond. The stone slides, slows down and eventually stops. You conclude that: 1) the force pushing the stone forward finally stopped pushing on it 2) no net force acted on the stone 3) a net force acted on it all along 4) the stone simply “ran out of steam” 5) the stone has a natural tendency to be at rest After the stone was kicked, no force was pushing it along! However, there must have been some force acting on the stone to slow it down and stop it. it This would be friction!! Follow-up: What would you have to do to keep the stone moving?

Concep. Test 4. 5 Force and Mass A force F acts on mass M for a time interval T, giving it a final speed v. If the same force acts for the same time on a different 1) 4 v 2) 2 v 3) v mass 2 M, what would be the 4) 1/2 v final speed of the bigger mass? 5) 1/4 v

Concep. Test 4. 5 Force and Mass A force F acts on mass M for a time interval T, giving it a final speed v. If the same force acts for the same time on a different 1) 4 v 2) 2 v 3) v mass 2 M, what would be the 4) 1/2 v final speed of the bigger mass? 5) 1/4 v In the first case, the acceleration acts over time T to give velocity v = a. T. In the second case, the mass is doubled, doubled so the acceleration is cut in half; half therefore, in the same time T, the final speed will only be half as much. Follow-up: What would you have to do to get 2 M to reach speed v ?

Concep. Test 4. 6 Force and Two Masses A force F acts on mass m 1 giving acceleration a 1. The same force acts on a different mass m 2 giving acceleration a 2 = 2 a 1. If m 1 and m 2 are glued together and the same force F acts on this combination, what is the resulting acceleration? F F F m 1 a 1 m 2 m 1 a 2 = 2 a 1 a 3 1) 3/4 a 1 2) 3/2 a 1 3) 1/2 a 1 4) 4/3 a 1 5) 2/3 a 1

Concep. Test 4. 6 Force and Two Masses A force F acts on mass m 1 giving acceleration a 1. The same force acts on a different mass m 2 giving acceleration a 2 = 2 a 1. If m 1 and m 2 are glued together and the same force F acts on this combination, what is the resulting acceleration? F m 1 a 1 F m 2 F = m 2 a 2 = (1/2 m 1 )(2 a 1 ) m 2 m 1 2) 3/2 a 1 3) 1/2 a 1 4) 4/3 a 1 5) 2/3 a 1 F = m 1 a 2 = 2 a 1 F 1) 3/4 a 1 Mass m 2 must be (1/2)m 1 because its acceleration was 2 a 1 with the same force. Adding the two masses together gives (3/2)m 1, leading to an a 3 acceleration of (2/3)a 1 for the same applied force. F = (3/2)m 1 a 3 => a 3 = (2/3) a 1

Concep. Test 4. 9 a Going Up I A block of mass m rests on the floor of 1) N > mg an elevator that is moving upward at 2) N = mg constant speed. What is the relationship between the force due to 3) N < mg (but not zero) gravity and the normal force on the 4) N = 0 block? 5) depends on the size of the elevator v m

Concep. Test 4. 9 a Going Up I A block of mass m rests on the floor of 1) N > mg an elevator that is moving upward at 2) N = mg constant speed. What is the relationship between the force due to 3) N < mg (but not zero) gravity and the normal force on the 4) N = 0 block? 5) depends on the size of the elevator The block is moving at constant speed, so it must have no net force on it. The forces v on it are N (up) and mg (down), so N = mg, mg just like the block at rest on a table. m

Concep. Test 4. 9 b Going Up II A block of mass m rests on the 1) N > mg floor of an elevator that is 2) N = mg accelerating upward. What is 3) N < mg (but not zero) the relationship between the 4) N = 0 force due to gravity and the 5) depends on the size of the elevator normal force on the block? a m

Concep. Test 4. 9 b Going Up II A block of mass m rests on the 1) N > mg floor of an elevator that is 2) N = mg accelerating upward. What is 3) N < mg (but not zero) the relationship between the force due to gravity and the normal force on the block? 4) N = 0 5) depends on the size of the elevator The block is accelerating upward, so it must have a net upward force The forces on it are N (up) and mg (down), so N must be greater than mg in order to give the net upward force! force Follow-up: What is the normal force if the elevator is in free fall downward? N m a>0 mg S F = N – mg = ma > 0 N > mg

Concep. Test 4. 10 Normal Force Below you see two cases: a physics student pulling or pushing a sled with a force F which is applied at an angle q. In which case is the normal force greater? 1) case 1 2) case 2 3) it’s the same for both 4) depends on the magnitude of the force F 5) depends on the ice surface Case 1 Case 2

Concep. Test 4. 10 Normal Force Below you see two cases: a physics student pulling or pushing a sled with a force F which is applied at an angle q. In which case is the normal force greater? 1) case 1 2) case 2 3) it’s the same for both 4) depends on the magnitude of the force F 5) depends on the ice surface Case 1 In Case 1, the force F is pushing down (in addition to mg), mg so the normal force needs to be larger In Case 2, the force F is pulling up, up against gravity, so the normal force is lessened Case 2

Concep. Test 4. 15 a Contact Force I If you push with force F on either the heavy box (m 1) or the light box (m 2), in which of the two cases below is the contact force between the two boxes larger? 1) case A 2) case B 3) same in both cases A m 2 F m 1 B m 2 m 1 F

Concep. Test 4. 15 a Contact Force I If you push with force F on either the heavy box (m 1) or the light box (m 2), in which of the two cases below is the contact force between the two boxes larger? 1) case A 2) case B 3) same in both cases The acceleration of both masses together A is the same in either case. But the contact force is the only force that accelerates m 1 m 2 F m 1 in case A (or m 2 in case B). Since m 1 is the B larger mass, mass it requires the larger contact force to achieve the same acceleration. Follow-up: What is the accel. of each mass? m 2 m 1 F

Concep. Test 4. 16 b Tension II Two tug-of-war opponents each 1) 0 N pull with a force of 100 N on 2) 50 N opposite ends of a rope. What is the tension in the rope? 3) 100 N 4) 150 N 5) 200 N

Concep. Test 4. 16 b Tension II Two tug-of-war opponents each 1) 0 N pull with a force of 100 N on 2) 50 N opposite ends of a rope. What is the tension in the rope? 3) 100 N 4) 150 N 5) 200 N This is literally the identical situation to the previous question. The tension is not 200 N !! Whether the other end of the rope is pulled by a person, or pulled by a tree, the tension in the rope is still 100 N !!