Lecture 4 Dynamic Programming Basic Algorithm Design Techniques

Lecture 4 Dynamic Programming

Basic Algorithm Design Techniques • Divide and conquer • Dynamic Programming • Greedy Analyzing running time Design algorithm • Common Theme: To solve a large, complicated problem, break it into many smaller sub-problems.

Dynamic Programming • Idea: Break the problem into many closely related sub-problems, memorize the result of the subproblems to avoid repeated computation.

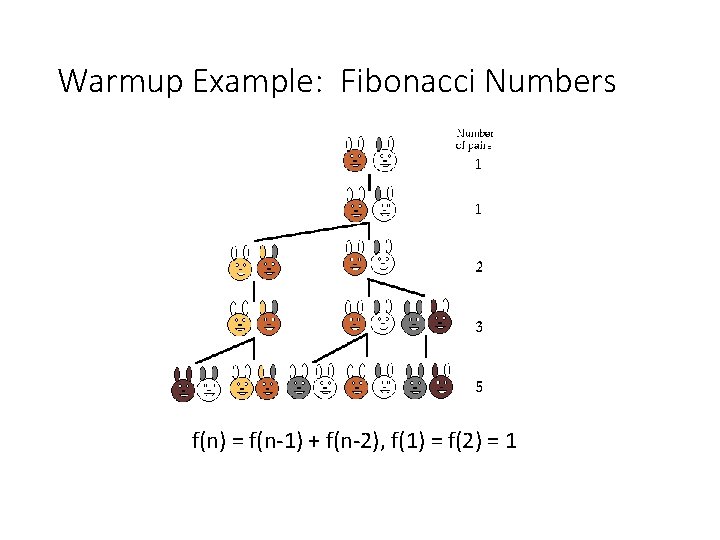
Warmup Example: Fibonacci Numbers f(n) = f(n-1) + f(n-2), f(1) = f(2) = 1

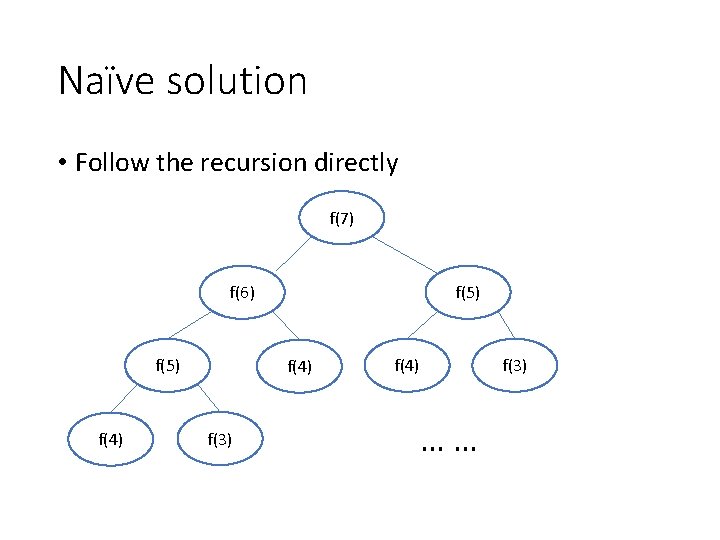
Naïve solution • Follow the recursion directly f(7) f(6) f(5) f(4) f(3) f(4) ……

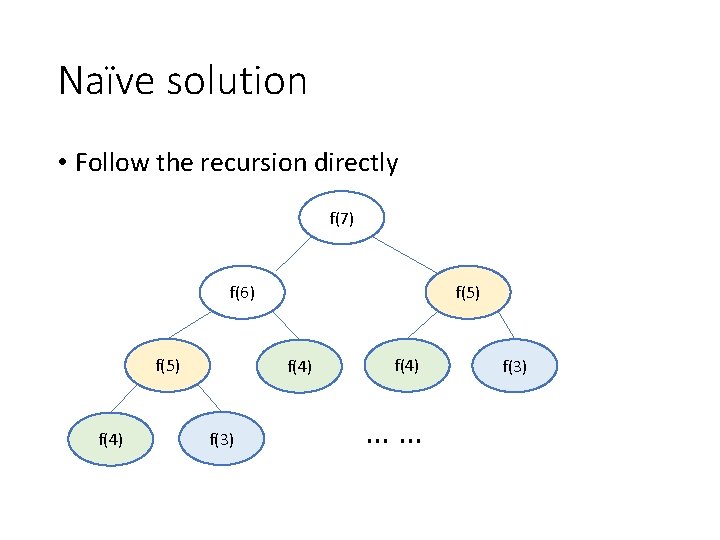
Naïve solution • Follow the recursion directly f(7) f(6) f(5) f(4) f(3) f(4) …… f(3)

Memoization f(n) 1. IF n < 3 THEN RETURN 1. 2. IF f(n) has been computed before THEN RETURN stored result. 3. res = f(n-1) + f(n-2) 4. Mark f(n) as computed, Store f(n) = res 5. RETURN res n 1 2 3 4 5 6 7 8 f(n) 1 1 2 3 5 8 13 21 Dynamic Programming Table

Filling in the table iteratively • Observation: f(n) is always computed in the order of n = 1, 2, 3, … • No need to recurse f(n) 1. IF n < 3 THEN RETURN 1. 2. a[1] = a[2] = 1 3. FOR i = 3 TO n 4. a[i] = a[i-1] + a[i-2] 5. RETURN a[n]

Basic Steps in Designing Dynamic Programming Algorithms • Relate the problem recursively to smaller subproblems. (Transition function, f(n) = f(n-1)+f(n-2)) • Organize all sub-problems as a dynamic programming table. (A table for all values of n) • Fill in values in the table in an appropriate order. (n = 1, 2, 3, …)

How to figure out the transition function • Often: need to think of the problem as making a sequence of decisions (i. e. , design a brute-force algorithm) • To find the transition function, enumerate all options for the last decision (rabbit + bunny) • For each option relate it to smaller subproblems (rabbit = f(n-1); bunny = f(n-2))

Example 1 Knapsack Problem • There is a knapsack that can hold items of total weight at most W. There are now n items with weights w 1, w 2, …, wn. Each item also has a value v 1, v 2, …, vn. • Goal: Select some items to put into knapsack 1. Total weight is at most W. 2. Total value is as large as possible.

Designing a DP algorithm for Knapsack • Step 1: think of the problem as making a seq. of decisions • For each item, decide whether we put it into the knapsack Knapsack(w[], v[], capacity) n = length(w[]) IF n == 0 THEN return 0 Ans = Knapsack(w[1. . n-1], v[1. . n-1], capacity) -- not putting last item in IF w[n] <= capacity THEN Alternative = Knapsack(w[1. . n-1], v[1. . n-1], capacity – w[n]) + v[n] -- putting last item in IF Alternative > Ans THEN Ans = Alternative RETURN Ans

Designing a DP algorithm for Knapsack • Step 1: think of the problem as making a seq. of decisions • For each item, decide whether we put it into the knapsack • Step 2: Focus on last decision, enumerate the options • For the last item, we either put it in, or leave it out. • Step 3: Try to relate each option to a smaller subproblem • Subproblem: Fill the remaining capacity using the remaining items • leave it out: number of items is now smaller. • put it in: reserve the capacity, both capacity and number of items are smaller.

States and Transition function • Example: Capacity W = 4, 3 items with (weight, value) = (1, 2), (2, 3), (3, 4). • States (sub-problems): What is the maximum value for a Knapsack with capacity j (= 0, 1, 2, 3, 4) and the first i (= 0, 1, 2, 3) items? • Use a[i, j] to denote this maximum value, we have a[i, j] = max a[i - 1, j - wi] + vi (item i in knapsack) a[i - 1, j] (item i not in knapsack)

Dynamic Programming Table • Example: Capacity W = 4, 3 items with (weight, value) = (1, 2), (2, 3), (3, 4). 0 1 2 3 4 0 0 0 1 0 2 2 2 0 2 3 5 5 3 0 2 3 5 6 +4

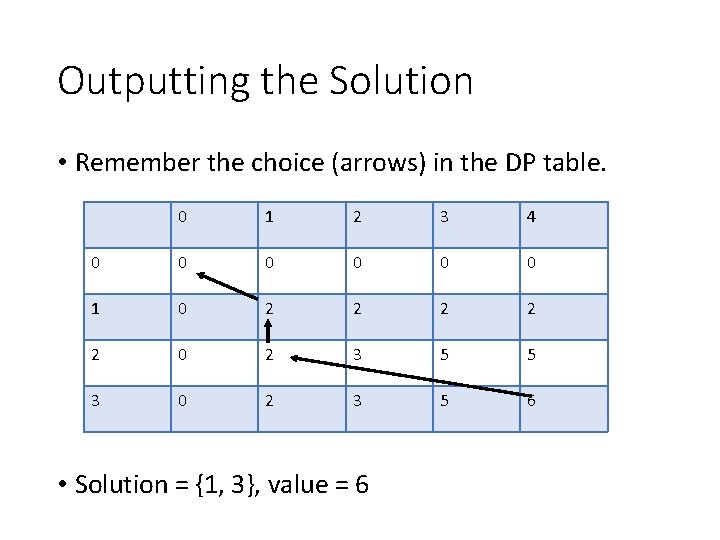
Outputting the Solution • Remember the choice (arrows) in the DP table. 0 1 2 3 4 0 0 0 1 0 2 2 2 0 2 3 5 5 3 0 2 3 5 6 • Solution = {1, 3}, value = 6

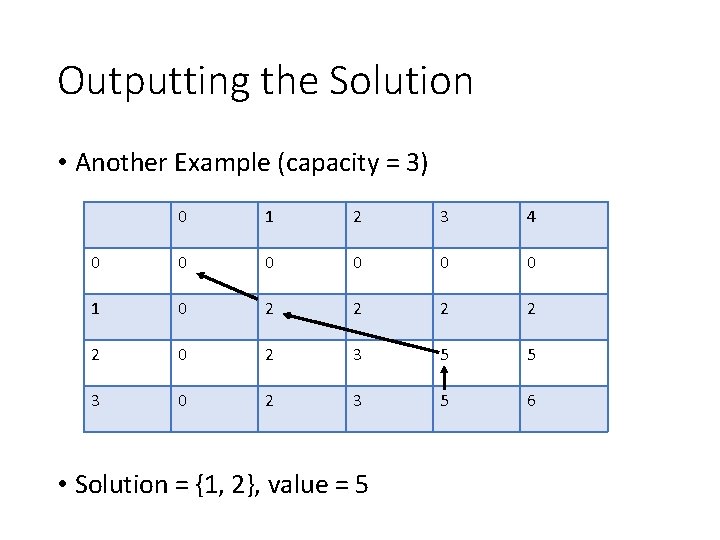
Outputting the Solution • Another Example (capacity = 3) 0 1 2 3 4 0 0 0 1 0 2 2 2 0 2 3 5 5 3 0 2 3 5 6 • Solution = {1, 2}, value = 5

Pseudo-code Knapsack 1. Initialize a[i, 0] = 0, a[0, j] = 0 (Base Case) 2. FOR i = 1 to n (Enumerate #items) 3. FOR j = 1 to W (Enumerate capacity) 4. a[i, j] = a[i-1, j] (Case 1: not using item i) 5. IF j >= w[i] and a[i-1, j-w[i]] + v[i] > a[i, j] (if Case 2 is better) 6. a[i, j] = a[i-1, j-w[i]] + v[i] (Case 2: using item i) Output(n, W) 1. IF n = 0 or W = 0 THEN RETURN 2. IF a[n, W] = a[n-1, W] THEN 3. Output(n-1, W) 4. ELSE 5. Output(n-1, W-w[n]) 6. Print(n) (Case 1) (Case 2)