Lecture 4 CS 1813 Discrete Mathematics Inference Rules

Lecture 4 CS 1813 – Discrete Mathematics Inference Rules, Dude 1

Definitions of Variables in Haskell double-hyphen starts comment x=3 -- defines x to be three xs = [4, 2, 9, 1] -- defines xs to be a sequence and. Commutes = Theorem [A `And` B] (B `And` A) -- defines and. Commutes to be a Theorem proof. And. Commutes = -- variable def’d to be Proof infix alternative (Assume(A `And` B) x `f` y means f x y {-----------}`And. ER` B, Assume(A `And` B) {-----------}`And. EL` A) {-------------------}`And. I` (B `And` A) indent to continue definition {- comment -} embedded comment first letter in variable: lowercase CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 2

Using Haskell from Windows importing de tools f’n s module Lecture 04 where ave ty import Stdm pin s g cp = check_proof comm = Theorem [A `And` B] (B `And` A) proof. Comm = (Assume(A `And` B) {-------------}`And. ER` B, Assume(A `And` B) {------------}`And. EL` A) {-------------------}`And. I` (B `And` A) Notepad window Gr e cm en i d f ndi rom cat use es Prelude> : cd DMs 05 r Prelude> : cd Lectures Prelude> : load lecture 04. hs Reading file "lecture 04. hs": Reading file "Stdm. lhs": Reading file "lecture 04. hs": Hugs session for: C: HUGS 98libPrelude. hs Stdm. lhs lecture 04. hs Main> cp comm proof. Comm The proof is valid Hugs Session CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 3

Incorrect Proof of Theorem q Theorem ( Commutes) § a b |– b a q Proof a b { EL} { ER} a b { I} b a Conclusion not in proper form (b and a in wrong positions to match I rule) a b { I} a b I rule CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 4

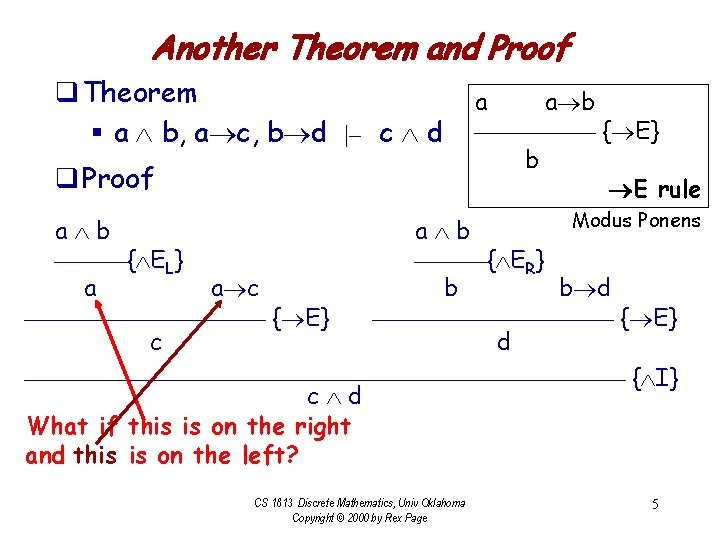
Another Theorem and Proof q Theorem § a b, a c, b d |– c d q Proof a a b { E} b E rule Modus Ponens a b { EL} { ER} a c b d a b { E} c d { I} c d What if this is on the right and this is on the left? CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 5

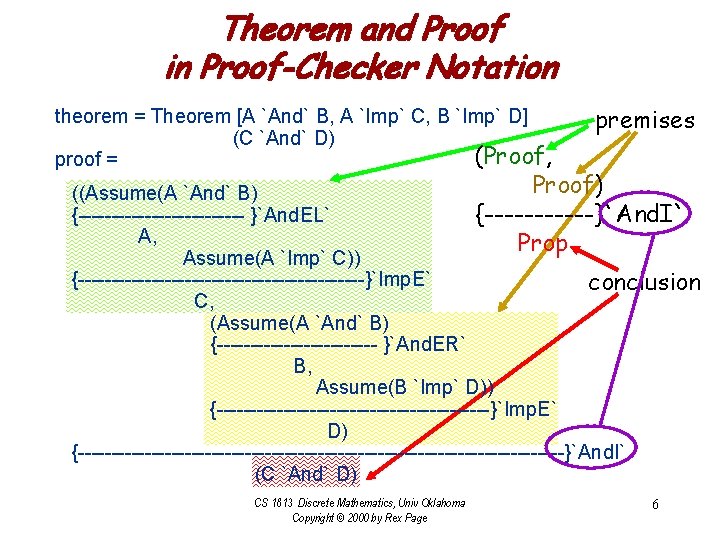
Theorem and Proof in Proof-Checker Notation theorem = Theorem [A `And` B, A `Imp` C, B `Imp` D] (C `And` D) (Proof, proof = premises Proof) ((Assume(A `And` B) {------------- }`And. EL` {------}`And. I` A, Prop Assume(A `Imp` C)) {----------------------}`Imp. E` conclusion C, (Assume(A `And` B) {------------ }`And. ER` B, Assume(B `Imp` D)) {---------------------}`Imp. E` D) {-------------------------------------}`And. I` (C `And` D) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 6

Inference Rules We’ve Used in Proofs a b { EL} a EL rule a b { ER} b ER rule a b { I} a b I rule a a b { E} b E rule And Elimination Right Latin name: Modus Ponens And Elimination Left And Introduction Implication Elimination How these rules work: If you have proofs of the propositions above the line (or if they are premises of theorem you are trying to prove), you can infer the proposition below the line. CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 7

Implication Introduction a different kind of animal a |– b { I} a b then you can infer the proposition. a b I rule If there is a proof of proposition b when you assume proposition, a What’s Different? Implication Introduction The assumed proposition, a, need not be a premise of theorem Nor does it have to be proved from the premises Temporary Admission The assumption a is temporarily “admitted” into the proof Later, when the { I} rule is invoked, the assumption a is discharged What! You can assume anything you want? Where’s the logic in that? The conclusion of the rule doesn’t require a to be true, or b either It only requires that if a were true, then b would also be true What happens to assumptions that aren’t discharged? They become premises of theorem (“permanent inmates” so to speak) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 8

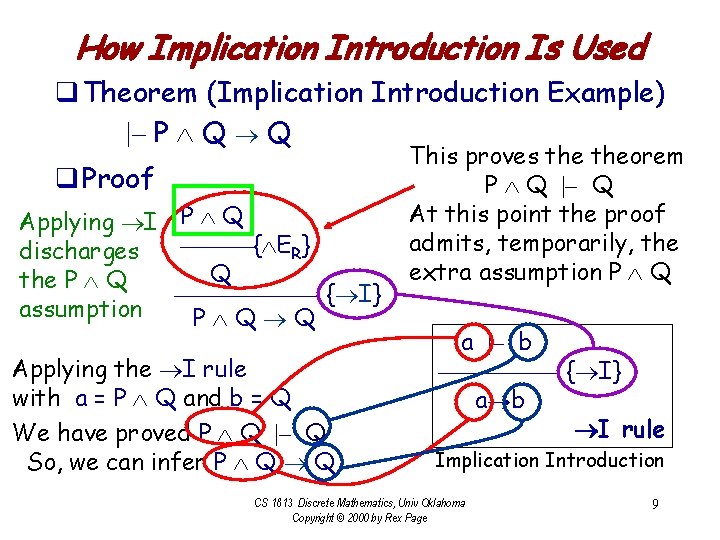
How Implication Introduction Is Used q Theorem (Implication Introduction Example) |– P Q Q q Proof Applying I P Q { ER} discharges Q the P Q { I} assumption P Q Q Applying the I rule with a = P Q and b = Q We have proved P Q |– Q So, we can infer P Q Q This proves theorem P Q |– Q At this point the proof admits, temporarily, the extra assumption P Q a |– b { I} a b I rule Implication Introduction CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 9

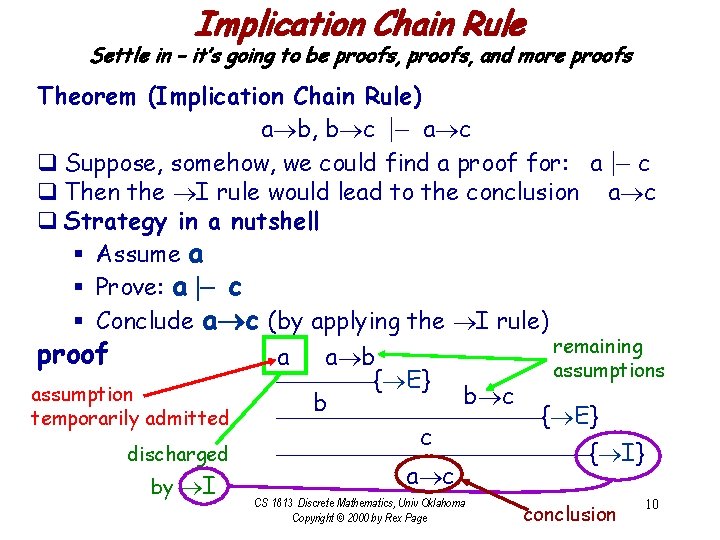
Implication Chain Rule Settle in – it’s going to be proofs, and more proofs Theorem (Implication Chain Rule) a b, b c |– a c q Suppose, somehow, we could find a proof for: a |– c q Then the I rule would lead to the conclusion a c q Strategy in a nutshell § Assume a § Prove: a |– c § Conclude a c (by applying the I rule) remaining proof a a b assumptions { E} assumption b c b { E} temporarily admitted c { I} discharged a c by I CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page conclusion 10

Getting the Parens and Commas Right in Proof-Checker Notation a { IL} (a b) False a b { E} False { I} a False ( ( (Assume A ) {--------}`Or. IL` ( A `Or` B ) ) , Assume((A `Or` B) `Imp` FALSE) ) {-------------------------------}`Imp. E` ( FALSE ) ) {----------------------------------}`Imp. I` ( A `Imp` FALSE ) ) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 11

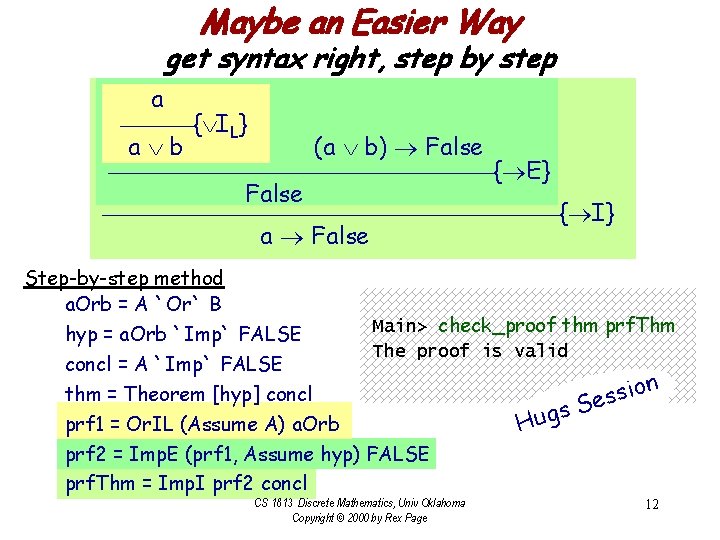
Maybe an Easier Way get syntax right, step by step a { IL} (a b) False a b { E} False { I} a False Step-by-step method a. Orb = A `Or` B Main> check_proof thm prf. Thm hyp = a. Orb `Imp` FALSE The proof is valid concl = A `Imp` FALSE on i thm = Theorem [hyp] concl s s Se s g prf 1 = Or. IL (Assume A) a. Orb Hu prf 2 = Imp. E (prf 1, Assume hyp) FALSE prf. Thm = Imp. I prf 2 concl CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 12

End of Lecture CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 13