Lecture 39 VIBRATIONS Springmass system undamped motion Now

Lecture 39 VIBRATIONS
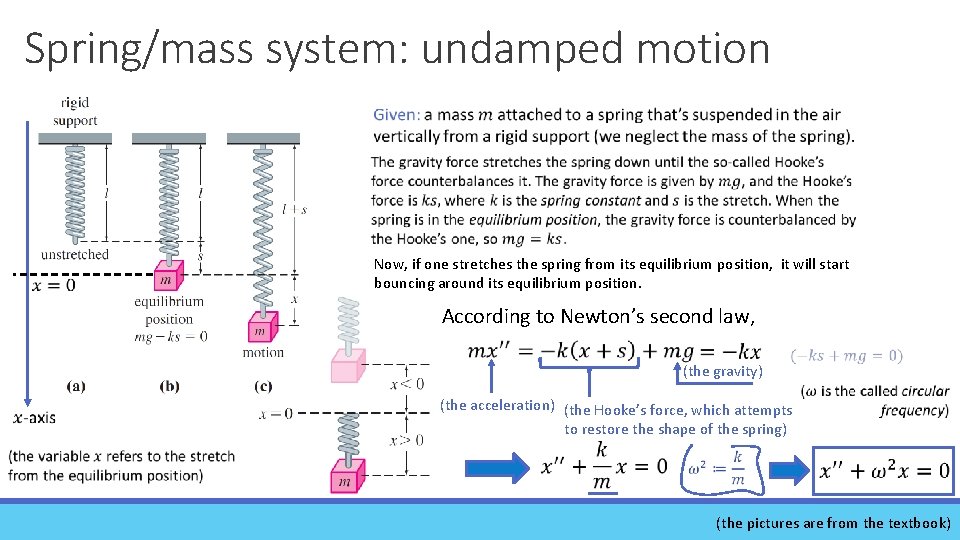
Spring/mass system: undamped motion Now, if one stretches the spring from its equilibrium position, it will start bouncing around its equilibrium position. According to Newton’s second law, (the gravity) (the acceleration) (the Hooke’s force, which attempts to restore the shape of the spring) (the pictures are from the textbook)
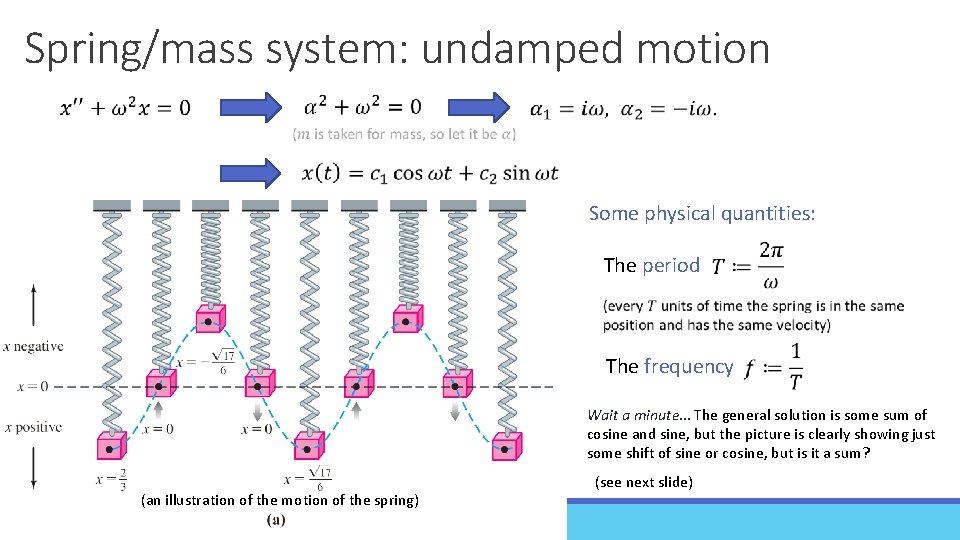
Spring/mass system: undamped motion Some physical quantities: The period The frequency Wait a minute… The general solution is some sum of cosine and sine, but the picture is clearly showing just some shift of sine or cosine, but is it a sum? (an illustration of the motion of the spring) (see next slide)

Let’s see how to convert the sum of cosine and sine into a single trig function. (can convert to) The idea: From geometry, The amplitude The phase angle

The amplitude determines the maximum possible stretch of the spring. (cosine and sine differ merely by a phase angle, that’s all the difference)

Spring/mass system: undamped motion continued Example. Solution. On the homework, convert everything into engineering units. (ft) (positive sign because released below) This is the displacement present in the Hooke’s law tha determines the equilibrium point: (lb/ft) The equation is

Spring/mass system: undamped motion continued Example. (ft)

Spring/mass system: damped motion For a free damped motion, we assume that the motion of the spring is in some viscous environment (or even just in water) that impedes the motion. Newton’s second law in this case: The damping force The roots of the auxiliary equation: brings convenience Depending on the three types of the roots, the system exhibits three different behaviors.

Analysis of the roots Case 1. The roots are real and distinct. Case 2. The roots are the same. Case 3. The roots are complex. Possible solutions: No oscillations, the spring slowly returns to the equilibrium (the environment is too viscous, for instance) The system is called overdamped. (a slight decrease in the damping constant results in an oscillatory behavior) (the system exhibits a decaying oscillatory behavior) The system is called critically damped. The system is called underdamped.

Driven motion A nonhomogeneous equation might arise when, for instance, the support for the spring oscillates itself. Newton’s second law: Example. Interpret and solve the initial-value problem Interpretation: The external periodic force The mass The damping constant What’s interesting: despite the damping, in this example the external force allows the spring to go on forever.

Driven motion continued Example. Interpret and solve the initial-value problem Solution. Normalize the equation: (interpreted on the previous slide) Let’s use undetermined coefficients method: (may go for Green’s function, but here it’s more complicated, for the integral in the end has the product of an exponential function and a trig function) … (the general solution)
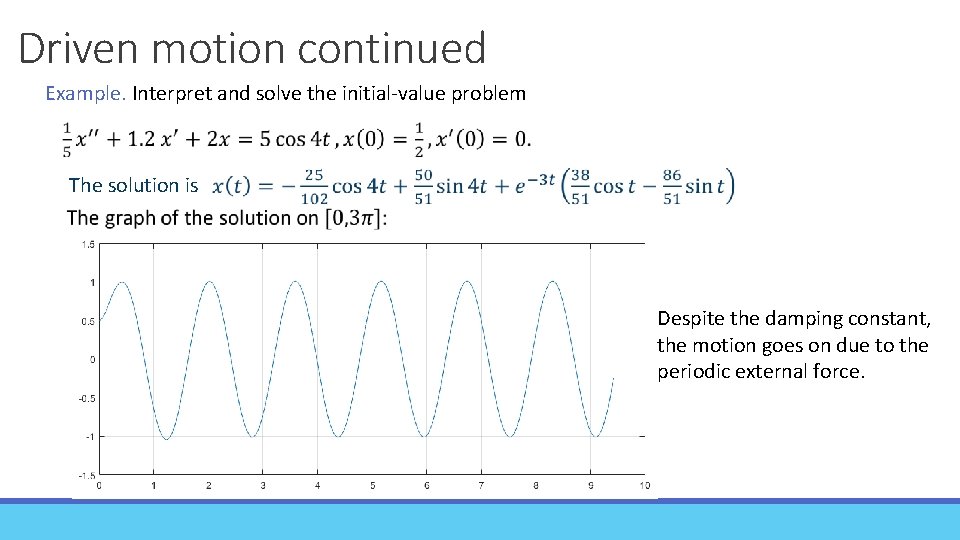
Driven motion continued Example. Interpret and solve the initial-value problem The solution is Despite the damping constant, the motion goes on due to the periodic external force.

Undamped forced motion Example. Solve the initial-value problem Solution. Let’s go for Green’s function. The Wronskian: The Green’s function:

Undamped forced motion Example. Solve the initial-value problem The first integral is: The second integral requires a certain care.
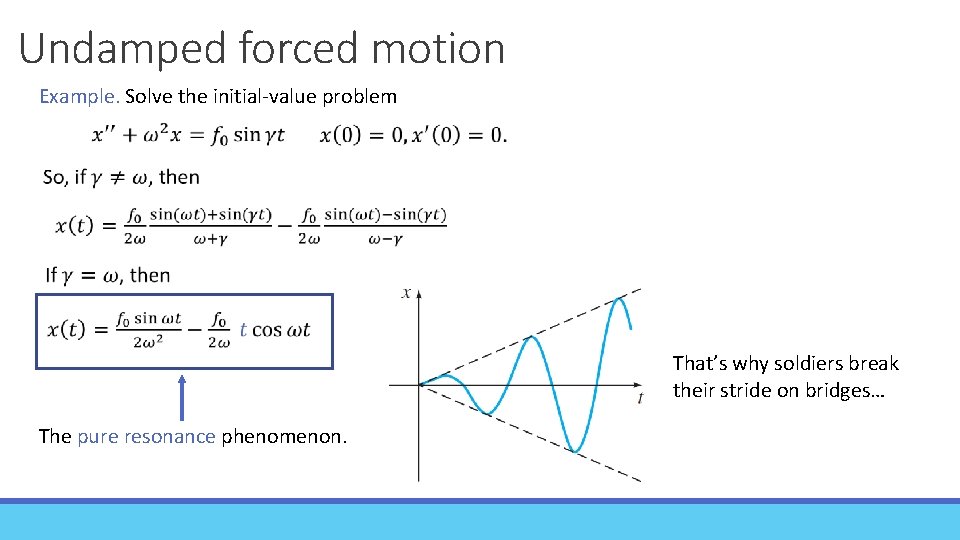
Undamped forced motion Example. Solve the initial-value problem That’s why soldiers break their stride on bridges… The pure resonance phenomenon.
- Slides: 15