Lecture 34 LINEAR HOMOGENEOUS ODES WITH CONSTANT COEFFICIENTS

Lecture 34 LINEAR HOMOGENEOUS ODES WITH CONSTANT COEFFICIENTS

Class Participation Question for 04/26 (all numbers and exponents are real) (don’t need to find the actual solutions, just pick the form they have)

(one obtains the formula by following the previous algorithm in the most general situation)

Linear Homogeneous ODE’s with constant coefficients Idea. Suppose we have the following DE: (the coefficients are constant) Linearly independent The general solution is

Case 1: real and distinct roots Solution. Solve an auxiliary quadratic equation: (the general solution) What if there is an IVP? (the solution of the IVP)

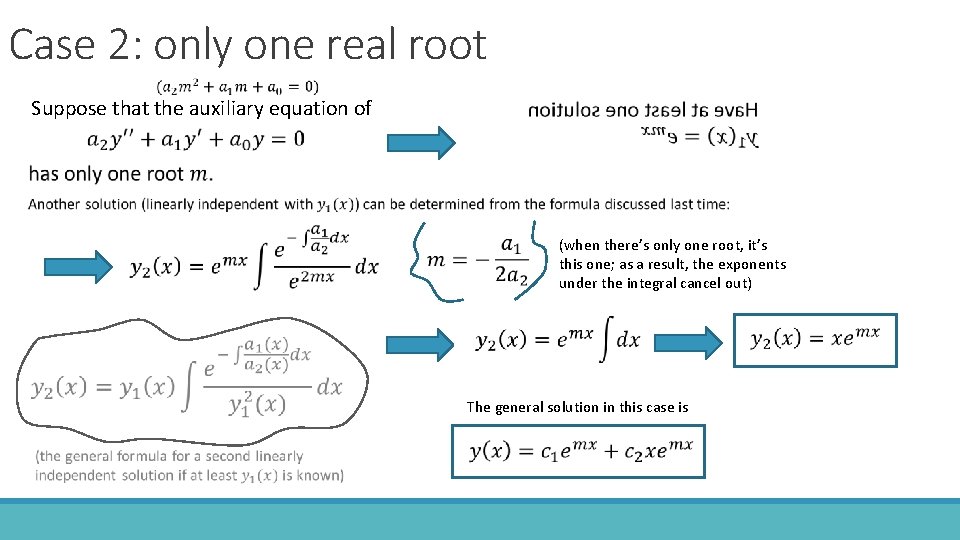
Case 2: only one real root Suppose that the auxiliary equation of (when there’s only one root, it’s this one; as a result, the exponents under the integral cancel out) The general solution in this case is

Case 2: only one real root continued Solution. Solve the auxiliary equation: (linearly independent solutions)

Case 3: complex roots (make a change of basis to make the basis real) (linearly independent, but complex-valued – less convenient to work with) (I use the same notation, those the functions now are different) (the general solution when the roots are complex)

Case 3: complex roots continued Solution. Solve the auxiliary equation: (a pair of linearly independent solutions for this case)

Other bases for the solution space Recall: (hyperbolic sine) (hyperbolic cosine) (so, can write solutions with respect to a different basis) (under the change of basis, with possibly different constants labelled by the same letters)

Other bases for the solution space continued Solution. (use IVP)

Higher order linear ODE’s with constant coefficients

Higher order linear ODE’s with constant coefficients Example. Find the general solution of assuming that the auxiliary equation has been already factorized as Solution. Collect the linearly independent functions corresponding to all factors:

Higher order linear ODE’s with constant coefficients Example. Find the general solution of assuming that the auxiliary equation has been factorized as