Lecture 3 Tools of the Trade High Energy

Lecture 3: Tools of the Trade • High Energy Units • 4 -Vectors • Cross-Sections • Mean Free Path Useful Sections in Martin & Shaw: Section 1. 5, Appendix A, Appendix B

High Energy Units (''natural" units) ''c = ℏ = 1" but really it’s just LYING! Say that you’re talking about mass, momentum, time and length but actually convert everything to units of energy using fundamental constants and pretend not to notice 1 e. V/c 2 = 1. 782 x 10 -36 kg m E E mc 2 L 1/E E = ℏc/ƛ p E E pc 1 e. V/c = 5. 346 10 -28 kg m/s t 1/E E=ℏ ℏ/t ℏ = 6. 58 10 -22 Me. V s ℏc/L ℏc = 197 Me. V fm (1 fm = 10 -15 m)

However The use of natural units is not always strictly followed and sometimes is even done in a mixed manner ! Basically, just look at what units you have and decide what units you would like given the nature of the quantity being calculated. Then just figure out what combinations of ℏ and c you need to get there Don’t worry the combination will be unique !

Example: Convert the following to MKS units of acceleration: 2. 18 x 10 34 Ge. V want to multiply by units ℏacb Ea Ta Lb. T b = Ea Ta-b Lb comparing a = 1 c = factor = ℏ ℏ ET c L T 1 LT 2 E 1 & b=1 3 x 108 m/s 6. 58 x 10 25 Ge. V s = 4. 5 x 1032 m/s 2/Ge. V (2. 18 x 10 34 Ge. V)(4. 5 x 1032 m/s 2/Ge. V) = 9. 8 m/s 2 = g

Steve’s Tips for Becoming a Particle Physicist 1) Be Lazy 2) Start Lying

4 -Momenta There are different formulations and different sign conventions used for this. . . so beware!! But (luckily) the basics are pretty straight-forward: Define the 4 -component vector P (E, px, py, pz) = (E, p) (''natural" units, otherwise E E/c) Define the scalar product of 2 such beasts as P 1 P 2 = E 1 E 2 - p 1 p 2 Note that this means P P = P 2 = E 2 - p 2 = m 2 true for the square of any linear combination of 4 -vectors! relativistic invariant !!

Basic Recipe Idea: 1) Represent the reaction in terms of 4 -momenta (statement of energy and momentum conservation) 2) Algebraically manipulate 4 -vectors to simplify and insure the result will be couched in terms of relevant angles, energies etc. 3) “Square” both sides of the equation, choosing convenient reference frames for each side 4) Let cool for 15 minutes and serve warm with plenty of custard and a nice, hot mug of tea

2 particle beams cross with angle . Find the total CM energy in the limit E≫m. What is this for a head-on collision? Example: p 1 LAB p 2 CM ( P 1 + P 2 )2 = PT 2 P 12 + P 22 + 2 P 1 · P 2 = PCM 2 PCM = (ECM, 0) m 12 + m 22 + 2 E 1 E 2 - 2 p 1 p 2 cos = ECM 2 – 02 for E≫m, ignore m 1 & m 2 and take p 1 E 1, p 2 ECM 2 = 2 E 1 E 2 (1 - cos ) = 2 E 1 E 2 (1 + cos ) so, for a head-on collision ECM ≈ 2(E 1 E 2)1/2

What is the threshold energy for antiproton production in the fixed target proton-proton collision: p + p + p ? Example: 1 P 1 +P 2 = PF 2 (fixed) 3 4 5 6 where: PF = (E 3+E 4+E 5+E 6 , p 3+p 4+p 5+p 6) = (4 m , 0) in CM at threshold p (P 1 + P 2)2 = PF 2 mp 2 + 2 E 1 E 2 – 2 p 1·p 2 = (4 mp)2 - (0)2 (in lab, p 2= 0 , so E 2=mp) 2 E 1 mp + 2 mp 2 = 16 mp 2 E 1 = 7 mp If target proton is moving with a kinetic energy of 30 Me. V, what is the threshold kinetic energy ? ( p 1 = E 12 - mp 2 = 6. 93 mp) T 2 = E mp = mp - mp = mp( 1) =1. 03 & = 0. 253 E = ( E p ) = 1. 03 (E 1 0. 253 p 1) = 5. 4 mp T 1 = E mp = 4. 4 mp

A high energy neutron travelling at velocity vn undergoes beta decay: n p + e + n e The opening angle of the charged particle products is measured, along with their energies. Determine the angle of the neutrino trajectory with respect to the incoming neutron direction. Example: ne n p Pn = Pp + Pe + Pn e (Pn )2 = ( P p + P e )2 Pn 2 + Pn 2 - 2(En. En - pnpncos ) = Pp 2 + Pe 2 + 2(Ep. Ee - pppecos ) mn 2 + 0 - 2 En(En - pncos ) = mp 2 + me 2 + 2(Ep. Ee - pppecos ) [mp 2 + me 2 - mn 2 + 2(Ep. Ee - pppecos )] cos = 2 pn. En = [mp 2 + - me mn 2 + 2(Ep. Ee 2 2 pn(En - Ep - Ee ) - pppecos )] En / pn ( m/ mv) vn

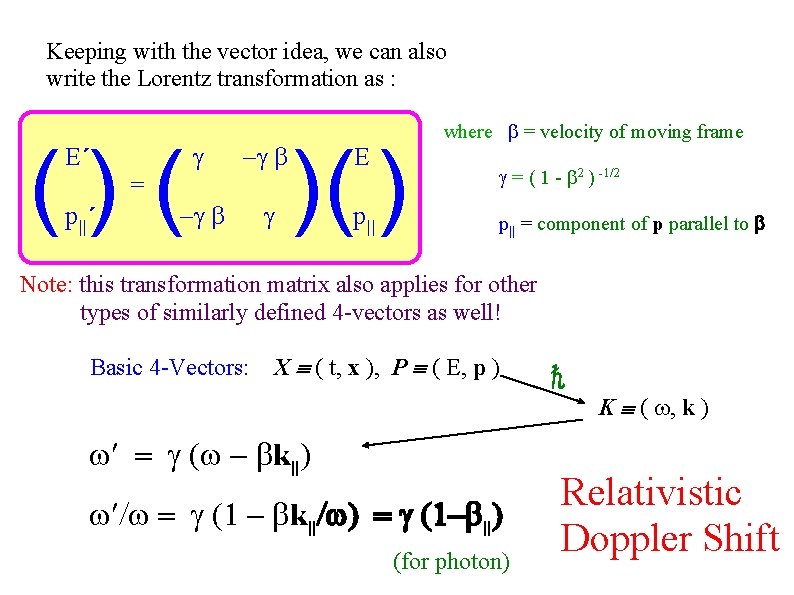
Keeping with the vector idea, we can also write the Lorentz transformation as : ( ) ( E´ = p||´ )( ) E p|| where = velocity of moving frame = ( 1 - 2 ) -1/2 p|| = component of p parallel to Note: this transformation matrix also applies for other types of similarly defined 4 -vectors as well! Basic 4 -Vectors: X ( t, x ), P ( E, p ) k||/w) = g (1 - ||) (for photon) ℏ K ( , k ) Relativistic Doppler Shift

More fun with 4 -Vectors! Start with X ( t, x ), P ( E, p ) Take time-derivative of X. . . but which “time? ” d/dt X = [(dt/dt d/dt) t, (dt/dt d/dt) x] = ( , v ) V Similary, d/dt P = ( d. E/dt, f ) F

3 sheet 1 Pions can decay via the reaction p+ ® m+ nm. Find the energy of the neutrino in the rest frame of the pion. Pp = P + Pn P = Pp - Pn rest frame (p & n in same frame) P 2 = Pp 2 + Pn 2 - 2 Pp· Pn p rest frame m 2 = mp 2 + 0 – 2(Ep. En – pp·pn) mp 2 - m 2 = 2(En Ep –pp·pn) = 2 Enmp En = (mp 2 - m 2 )/2 mp

3 sheet 1 Derive an expression relating the emission angle of the muon or neutrino with respect to the beam in the CM to that in the lab frame. Transverse momentum: CM frame lab frame plabsin = pcmsin p. CM plab Longitudinal momentum: plabcos = (pcmcos + Ecm divide: tan = sin [ (cos + Ecm/pcm ] pcm/Ecm = p (particle) = sin [ (cos + / p ] Are there any limits to the lab directions of the muon or neutrino? To find maximum angle, set d /d = 0 cos max = - p Thus, a solution is well defined if p < , or if > p Not possible for n since p (i. e. no restriction), but a restriction is possible for

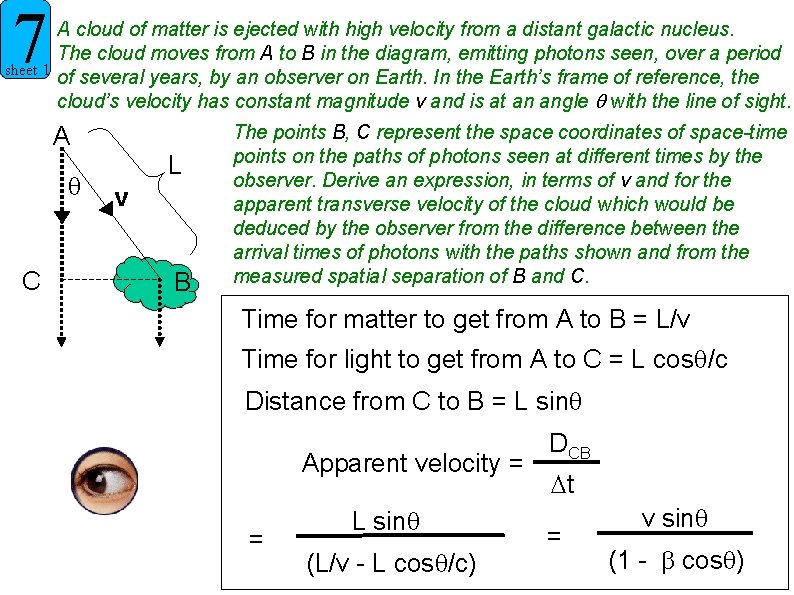
7 sheet 1 A cloud of matter is ejected with high velocity from a distant galactic nucleus. The cloud moves from A to B in the diagram, emitting photons seen, over a period of several years, by an observer on Earth. In the Earth’s frame of reference, the cloud’s velocity has constant magnitude v and is at an angle with the line of sight. A C L v B The points B, C represent the space coordinates of space-time points on the paths of photons seen at different times by the observer. Derive an expression, in terms of v and for the apparent transverse velocity of the cloud which would be deduced by the observer from the difference between the arrival times of photons with the paths shown and from the measured spatial separation of B and C. Time for matter to get from A to B = L/v Time for light to get from A to C = L cos /c Distance from C to B = L sin Apparent velocity = = L sin (L/v - L cos /c) DCB t = v sin (1 - cos )

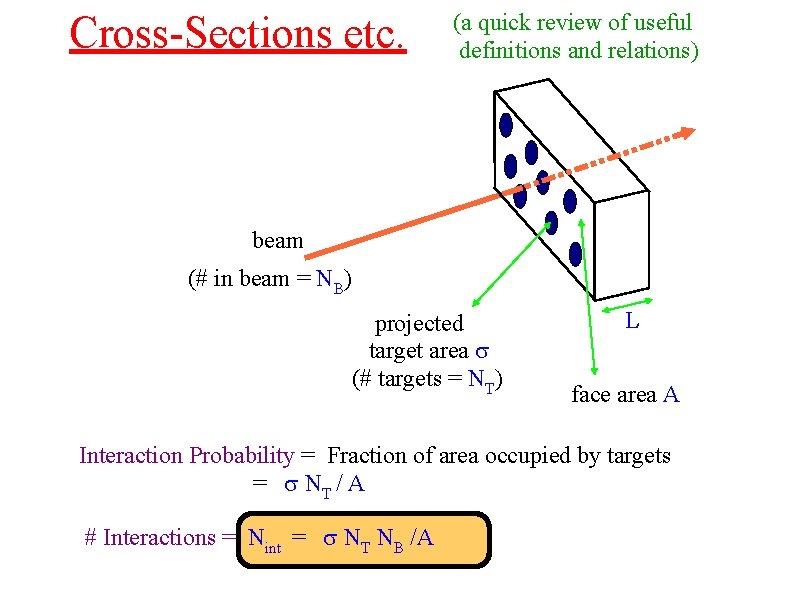
Cross-Sections etc. (a quick review of useful definitions and relations) beam (# in beam = NB) projected target area (# targets = NT) L face area A Interaction Probability = Fraction of area occupied by targets = NT / A # Interactions = Nint = NT NB /A

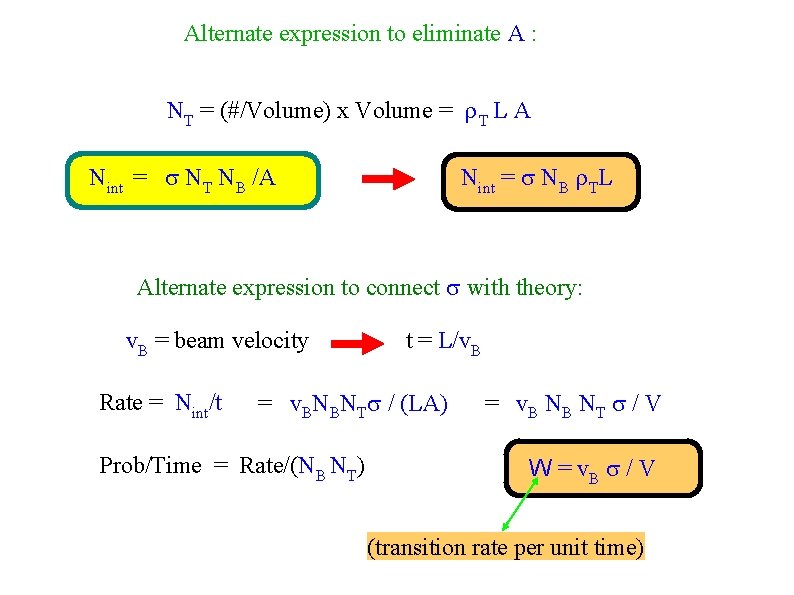
Alternate expression to eliminate A : NT = (#/Volume) x Volume = L A Nint = NT NB /A Nint = NB L Alternate expression to connect with theory: v. B = beam velocity Rate = Nint/t t = L/v. B = v. BNBNT / (LA) Prob/Time = Rate/(NB NT) = v. B NB NT / V W = v. B / V (transition rate per unit time)

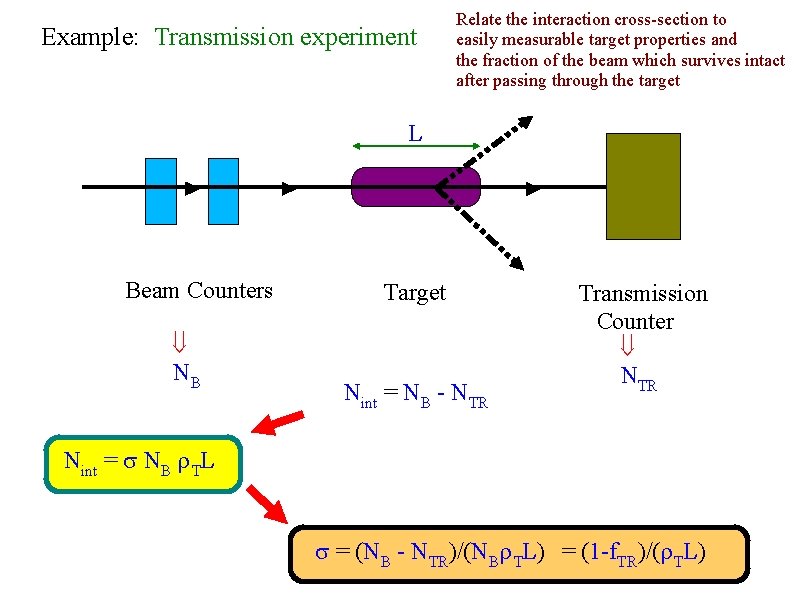
Example: Transmission experiment Relate the interaction cross-section to easily measurable target properties and the fraction of the beam which survives intact after passing through the target L Beam Counters NB Target Nint = NB - NTR Transmission Counter NTR Nint = NB L = (NB - NTR)/(NB L) = (1 -f. TR)/( L)

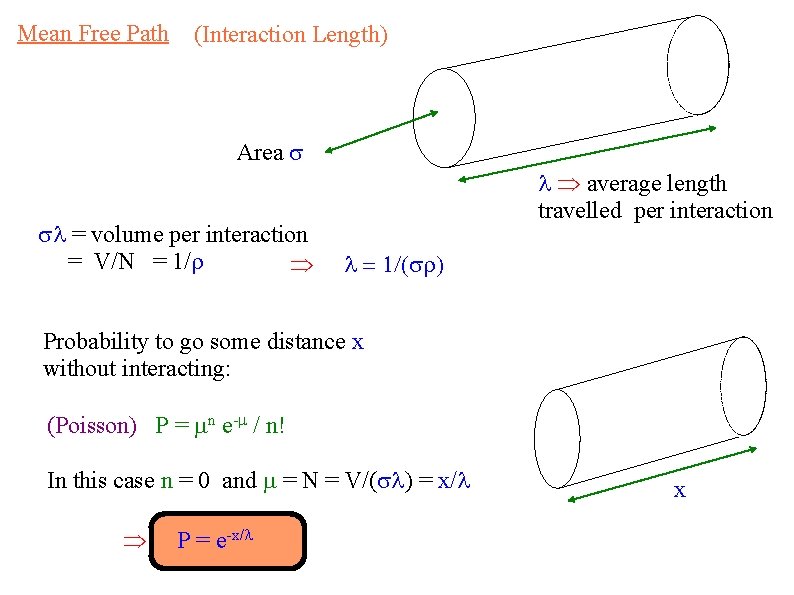
Mean Free Path (Interaction Length) Area = volume per interaction = V/N = 1/ average length travelled per interaction Probability to go some distance x without interacting: (Poisson) P = n e- / n! In this case n = 0 and = N = V/( ) = x/ P = e-x/ x