Lecture 3 SQL Aggregate Operators GROUP BY and

Lecture 3 • SQL – – – Aggregate Operators GROUP BY and HAVING Arithmetic, AS in SELECT DDL Set theory operators in SQL Subqueries • Relational Algebra – – 3/11/2021 Join queries Set queries Rename operator Divide operator Slide 1

Learning Objectives • LO 2. 1 Write SQL queries involving GROUP BY and HAVING. • LO 2. 2 Write an SQL query involving set operators. • LO 2. 3 Write an SQL query involving a subquery. • LO 2. 4 Tell whether an SQL subquery is correlated. • LO 2. 5 Write join queries in relational algebra • LO 2. 6 Write set operator queries in relational algebra 3/11/2021 Slide 2

Aggregate Operators • Let's return to the cl tables in your handout. • Find the number of donations, the largest, the smallest and the average donation. SELECT COUNT(*), MAX(amount), MIN(amount), AVG(amount) FROM indivcl; count max 21 3550 min 200 avg 631. 9047619048 – round(AVG(amount), 2) will get rid of all those significant digits. 3/11/2021 Slide 3

Aggregates with DISTINCT* • What is the difference between SELECT COUNT(street 1) FROM commcl; • and SELECT COUNT(DISTINCT street 1) FROM commcl; 3/11/2021 Slide 4

Bad SQL* • What are the occupations of donors who gave the highest donations? • This SQL doesn't make sense because the query processor has no way to know which values of occup to list with the MAX value of amount. • What if the aggregate function were AVG? • So if one aggregate operator appears in the SELECT clause, then ALL of the entries in the select clause must be aggregate operators (unless the query includes a GROUP BY clause - covered next). 3/11/2021 Slide 5

French Fries Warmup-1* 3/11/2021 Slide 6

GROUP BY • Here is the SQL for that query: SELECT month, MAX(amount) 3 For each month, compute the values in the SELECT clause FROM indivcl 1 Gather rows from indivgb GROUP BY month 2 Create groups, one for each GROUP BY value 3/11/2021 Slide 7

French Fries Warmup-2* 3/11/2021 Slide 8

SQL for this query: HAVING SELECT commid, SUM(amount) 5 For each committee, compute the values in the SELECT clause FROM indivgb 1 Gather rows from indivgb WHERE amount > 200 2 Keep rows satisfying the WHERE condition GROUP BY commid 3 Create groups, one for each GROUP BY value HAVING COUNT(*) > 5; 4 Keep groups satisfying the HAVING condition 3/11/2021 Slide 9

Practice Group By/Having* • Back to the indivcl on your handout. What is the SQL for: • For commitees that received at least three donations in March, how many donations did they receive? 3/11/2021 Slide 10

3/11/2021 Slide 11

LO 2. 1: GROUP BY/HAVING • Consider only donations in February and March. For each committee that had at least $2500 in donations, display that committee's range* of donations. *range = highest - lowest 3/11/2021 Slide 12

Arithmetic and AS in SELECT commcl. commid, commname, MAX(amount) - MIN(amount) AS Range Arbitrary arithmetic is possible in the SELECT clause. AS is used to label output columns. FROM commcl JOIN indivcl USING (commid) WHERE month = 2 OR month = 3 donations in February and March GROUP BY commcl. commid, commcl. commname must be here to be in the SELECT clause HAVING(SUM(amount)>=2500); any group condition can be in the HAVING clause 3/11/2021 Slide 13

NULLs and Aggregates • The value NULL is ignored by all aggregate functions. COUNT, SUM, AVG all ignore it, and it cannot be the MIN or MAX. COUNT(*) is the number of rows but COUNT(att) is the number of rows with non-null att values. • However, if you GROUP BY an attribute, a separate group is created for NULL values of the attribute. • So you don't like NULL and vow never to insert NULL values in your database? Sorry. If you aggregate (except count) over an empty table, you get NULL. There's no way to avoid it. 3/11/2021 Slide 14

Return to DDL: Populating a Database • Recall that SQL consists of DDL and DML. • We've been learning DML. • Let's digress for a bit and learn some more DDL, by reviewing the code for populating the Postgre. SQL database we're using. – Related to ETL in data warehousing • Populating a database consists of these steps (my files) 0. Format and clean the data (u 2 uc) 1. Create the schema (Tables. sql) 2. Copy the data into the database (cs) 3. Create structures and other tables (DDL. sql) 3/11/2021 Slide 15

0. Format and clean the data (u 2 uc) • The first step does not involve DDL • The shell script u 2 uc prepares files for copying into Postgre. SQL. – unzip: decompress • FEC compresses the data for faster data transfer and cheaper storage – dos 2 unix: remove carriage return • The parameter -437 suppresses an error message – pit: C program to insert delimiter | between fields – split -100000: writes a file into 100000 line pieces (xaa, xab, …) so it can be edited u 2 uc Document in http: //www. cs. pdx. edu/~len/386/fec/Mats. sql 3/11/2021 Slide 16

1. Create the schema (Tables. sql) • The next step is to create schemas for all the FEC tables. This is done in Tables. sql. • Note these DDL statements: – DROP TABLE [IF EXISTS] tablename; – CREATE TABLE tablename ( [ attributename domain [ [NOT] NULL], …. ] ) • For domains see http: //www. postgresql. org/docs/8. 3/interactive/datatype. html • CREATE TABLE has many other options, see documentation. • As we have discussed, for efficiency reasons, we don't use any of those other options until after the copy step. Tables. sql Document in http: //www. cs. pdx. edu/~len/386/fec/Mats. sql 3/11/2021 Slide 17

Sidebar on DROP TABLE tablename; is not the same as DELETE FROM tablename; • The former deletes the table's rows and all its structure – it no longer exists. The latter just deletes the rows. There is a shorter way to delete the rows: TRUNCATE tablename; • DROP applies to many objects: databases, schemas, constraints, views, etc, and these depend on each other. So SQL 3 requires that you specify either CASCADE or RESTRICT, though no DBMS does. – CASCADE: drop everything that depends on it. • For example, a foreign key dependency – RESTRICT: if anything depends on it, do not execute the command (typically the default). 3/11/2021 Slide 18

2. Copy the data into the database (cs) • There are two COPY commands in Postgre. SQL, one in SQL and another in psql. • psql executes in the address space of the DBMS • We use the psql version because CAT's databases are on a remote server. • The COPY commands are invoked from a shell script, cs, which takes as a parameter part of the name of the database, e. g. , $ cs 386 • Note that blank princomm or assoccand values are changed to NULL. cs Document in http: //www. cs. pdx. edu/~len/386/fec/Mats. sql 3/11/2021 Slide 19

3. Create structures and other tables (DDL. sql): INTO, IN • Now that we have copied data into the database, we use ALTER TABLE to change the database schema, and SELECT … INTO to create new tables. • First we ALTER TABLE tablename DROP column; to get rid of filler columns. • We will discuss the stored procedure next week; • Skip to Oregon versions. Notice INTO…. , which can appear after any SELECT clause. – INTO creates a new table with attributes from the SELECT clause. – An error is raised if a table with that name exists. – Results are not returned to the user. DDL. sql Document in http: //www. cs. pdx. edu/~len/386/fec/Mats. sql 3/11/2021 Slide 20

DDL. sql, Ctd. • In the in class versions, notice the use of IN. It can be used in any WHERE clause – IN is true when the left side is contained in the right side • Notice how a primary key constraint is declared – Recall that those columns were declared NOT NULL in the CREATE TABLE statements. • Why do we give a name to the constraints? – Can easily DROP them or ALTER them later. • Notice the foreign key constraints, which we have discussed. 3/11/2021 Slide 21

Set Operators in SQL • We now turn to set operators in SQL: UNION, INTERSECT, Difference (in SQL this is called EXCEPT or MINUS). • Suppose A, B are sets. What is the definition of – A UNION B, A∪B? – A INTERSECT B, A B? – A MINUS B, A – B? • You've seen these operators in CS 250, but here they operate on multisets. So they come in two versions. UNION, INTERSECT and EXCEPT/MINUS eliminate duplicates. Each of them with ALL preserve duplicates. • Let's see how they work. 3/11/2021 Slide 22

UNION • Let’s consider the entire FEC data: cand, comm, indiv, pas. • Suppose I have a table indivlast, leftover from the last time I taught the course, representing donations from the 2006 election. I want to combine it with indiv and display all the results. The proper SQL to do that is: SELECT * FROM indiv UNION SELECT * FROM indivlast • The UNION appears between any two SQL statements. • The output of the SQL statements must be UNION-Compatible: – Domains of corresponding attributes must be the same • Names don't need to be the same. The names of the first table are used in the output. – SELECT * from indivcl UNION SELECT * FROM commcl is illegal. 3/11/2021 Slide 23

Surprise! (UNION ALL) • Suppose we want to simplify the result by omitting the date: SELECT fecid, commid, occup, month, amount FROM indivlast UNION SELECT fecid, commid, occup, month, amount FROM indiv • We'll be surprised to learn that this time we have fewer donations! • UNION eliminates duplicates. • To avoid duplicate elimination, use UNION ALL. 3/11/2021 Slide 24

Subquery in FROM Clause • The previous UNION statements have displayed results on the screen. Suppose I want to place results in indivnew. SELECT * INTO indivnew FROM ( Subquery (SELECT * FROM indiv) UNION (SELECT * FROM indivlast) ) AS indiv_union; • Note the "subquery" in the FROM clause, enclosed in parens. – Any expression, whose result is a table, is legal as a term (comma-separated) in the FROM clause. – SQL requires a range variable after a FROM subquery. 3/11/2021 Slide 25

INTERSECTION* • Is this query legal? SELECT princomm FROM candcl WHERE party = 'REP' INTERSECT SELECT commid FROM indivcl where month = 1; • Identify one row in the answer to this query. • Describe, in nontechnical English, what this query produces: • INTERSECT eliminates duplicates, but INTERSECT ALL will retain them. 3/11/2021 Slide 26

EXCEPT (or MINUS)* • Identify one row in the answer to this query. • In nontechnical English, what does this query retrieve? SELECT commid FROM commcl EXCEPT SELECT commid FROM indivcl WHERE month=2; • EXCEPT eliminates duplicates, but EXCEPT ALL will retain them 3/11/2021 Slide 27

Example* • In indivcl, which unique committees received donations in January OR in February? Write the answer in three different ways, one with and two without a set operator. Order the results by commid. 3/11/2021 Slide 28

LO 2. 2: Example* • In indivcl, which unique committees received donations in January AND in February? Write the answer in two different ways, with and without a set operator. 3/11/2021 Slide 29

SUBQUERIES (in the WHERE Clause)* • The circled expression, a complete SELECT. . FROM. . WHERE query, is called an inner block or subquery. The rest is the outer block. • Describe what this query retrieves. Hint: First figure out what the subquery retrieves. • Note that the scope of the range variable in the subquery overrides that of the outer query. SELECT occup FROM indivcl WHERE amount = (SELECT MAX(amount) FROM indivcl) • How would you execute this query? 3/11/2021 Slide 30

LO 2. 3: Practice Subqueries* • Write the SQL to return the occupations of donors who gave donations (at any time) of at least $500 more than the minimum donation given during March. 3/11/2021 Slide 31

IN and subqueries • You've seen IN, in the definition of the cl tables, e. g. : SELECT candid, candname, party, street 1, princomm INTO candcl FROM cand WHERE candid IN ('P 80003338', 'P 80002801' , 'S 6 OR 00094' , 'S 8 OR 00207') ; • IN can also precede a subquery: SELECT commname FROM commcl m WHERE m. commid IN ( SELECT i. commid FROM indivcl i WHERE amount > 1000); • What does this query return? • How would you execute this query? • NOT IN is also legal in a query 3/11/2021 Slide 32

LO 2. 4: Unnesting/Flattening a Query* • Queries with subqueries are called nested queries. • Often they can be rewritten as flat queries. – This typically makes them much faster to execute • Can you write a flat version of the previous query? SELECT commname FROM commcl m WHERE m. commid IN ( SELECT i. commid FROM indivcl I WHERE amount > 1000); • Hint: Think of what it returns, then write that query. • Why do you need DISTINCT in the flat version? • Often the nested version is easier to write. 3/11/2021 Slide 33

EXISTS* • What does this query return? SELECT N. candname FROM candcl N WHERE EXISTS ( SELECT * FROM commcl M WHERE M. assoccand = N. candid AND M. street 1 LIKE '228 S WASHINGTON ST%'); • How would you execute this query? • Because of N. candid, you cannot substitute a constant for the subquery • Such a query is called correlated. 3/11/2021 Slide 34

Review, Preview • We are working with structured data, modeled with the relational model. • Databasics Anonymous 7 -step method: 1. 2. 3. 4. 5. Next Done Organizing structured data into an ER Diagram, Ch. 2 Transforming an ER diagram into a Schema of Tables, Ch. 3 Eliminating anomalies from those tables (normalization), Ch. 21 Structuring those tables efficiently (physical design), Ch. 22 Done Managing those tables using the intergalactic standard language (SQL), Ch. 5 • The DBMS manages the tables internally using Relational Algebra, Ch. 4 6. Protecting those tables during concurrent use (ACID properties), Ch. 16 7. Accessing those tables through a web-based interface (some scripting language) • Now we continue step 5 and study Relational Algebra. 3/11/2021 Slide 35

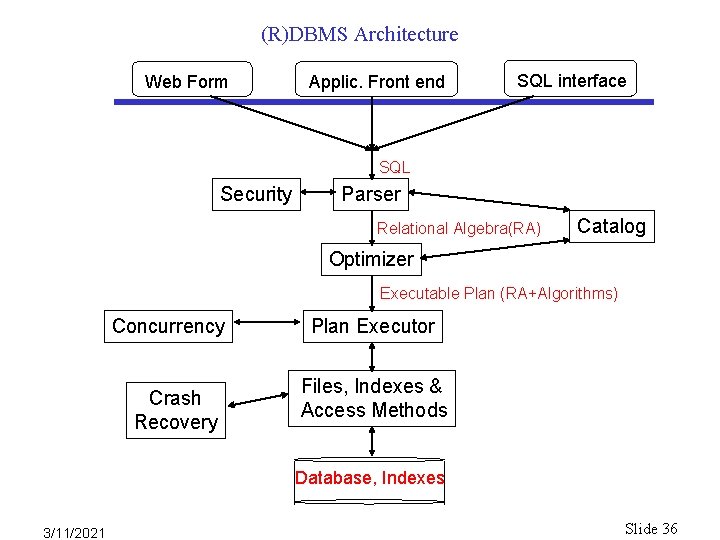
(R)DBMS Architecture Web Form Applic. Front end SQL interface SQL Security Parser Relational Algebra(RA) Catalog Optimizer Executable Plan (RA+Algorithms) Concurrency Crash Recovery Plan Executor Files, Indexes & Access Methods Database, Indexes 3/11/2021 Slide 36

Relational Algebra: 5 Basic Operations • Select( ) Selects a subset of rows from a table (horizontal) • Project( ) Selects a subset of columns from a table (vertical) • Cross-product( ) Computes all combinations from two tables • Set-difference ( ) Rows in table 1, not in table 2 • Union ( ) Rows in table 1 and/or in table 2 3/11/2021 Slide 37

Algebra • Relational Algebra is an algebra of operators on tables – Input is (a) table(s), output is a table • Just as plus, minus, multiply, divide are an algebra of operators on numbers • Since each relational algebra operation produces a table, the relational algebra is closed. 3/11/2021 Slide 38

Select ( ) • Consider the indivcl table in the handout. Suppose we want to find donations of more than $2000. • We construct the answer with the query amount > 2000 indivcl, whose output is fecid 1810515 1480419 3/11/2021 commid C 00383554 C 00430470 occup month PACIFIC CREST/PRINCIPLE 3 SELF-EMPLOYED 2 amount 3550 2300 Slide 39

Examples using the Select Operator* How many rows are in the output of each query? amount <= 225 indivcl The predicate (amount > 2000) (commid=‘C 00383554’) indivcl (commid=‘C 00431445’) (amount > 1000) indivcl • Is there a simple way to calculate this? (amount > 1000) ( (commid=‘C 431445’) indivcl ) 3/11/2021 An algebraic expression Slide 40

Project operator ( ) in relational algebra • Which committees received donations from 97223 in the period January-April 2008? commid(indivcl) • This query will produce 21 rows, with many Comm. IDs repeated – like the Recipient table we saw previously. 3/11/2021 Slide 41

The Project operator in the Relational Model and in DBMSs • The project operator in the relational model operates on relations (sets), so the project operator in the relational algebra eliminates duplicates. • But the project operator in DBMSs, operating on tables/multisets, does not eliminate duplicates. • In this class we will study relational algebra on tables, so project does not eliminate duplicates. 3/11/2021 Slide 42

Smart question • At this point some smart person in class will ask: in DBMSs, how do you eliminate duplicates from a multiset of data items? • There is a duplicate elimination operator. It is a terribly important, and expensive, operator, like sorting, but it changes only the presentation properties of the data. • We will introduce these two operators later, when we talk about algorithms for RA operators. 3/11/2021 Slide 43

Practice with , * • Show the IDs of our 4 candidates and their principal committees • Show the occupations of donors who donated at least $500 • Show the committees that received donations of more than $200. 3/11/2021 Slide 44

Equivalent Queries* • Describe in English the output of this query occup( amount < 1000 indivcl) • Which of these queries is equivalent to the above query, i. e. gives the same output for all table instances? amount < 1000( occup, amountindivcl) amount < 1000( occupindivcl) occup( amount < 1000( occup, amountindivcl)) 3/11/2021 Slide 45

The Cross Product Operator, • All our previous operators are unary operators, they operate on one table. The cross product operator is our first binary operator and is fundamental to most other binary operators. • T 1 T 2 is every possible combination of rows from T 1 and T 2. For example T 1 candid P 80002801 P 80003338 S 6 OR 00094 S 8 OR 00207 T 1 T 2 candname T 2 MCCAIN, JOHN S. OBAMA, BARACK SMITH, GORDON MERKLEY, JEFFREY candid candname P 80002801 P 80003338 S 6 OR 00094 S 8 OR 00207 MCCAIN, JOHN S. OBAMA, BARACK SMITH, GORDON MERKLEY, JEFFREY 3/11/2021 commid commname C 00003418 REPUBLICAN NATIONAL COMMITTEE C 00000936 DEMOCRATIC NATIONAL COMMITTEE commid commname C 00003418 REPUBLICAN C 00000936 DEMOCRATIC NATIONAL NATIONAL COMMITTEE COMMITTEE Slide 46

The Join Operator, ⋈ • Suppose we want to list each candidate’s name along with his/her principal committee’s name. • We want to combine a candidate row n in candcl with a committee row m in commcl if n. princomm = m. commid • Try it on a few row pairs (n, m). • The notation for the required query is: candname, commname( candcl ⋈ princomm=commid commcl ) • And its output is: candname MCCAIN, JOHN S. OBAMA, BARACK SMITH, GORDON MERKLEY, JEFFREY 3/11/2021 Joining condition commname JOHN MCCAIN 2008 INC. OBAMA FOR AMERICA FRIENDS OF GORDON SMITH JEFF MERKLEY FOR OREGON Slide 47

LO 2. 5 Practice with Join* • Describe in English what this computes: commname, candname(commcl ⋈ assoccand=candidcandcl) • Write a query describing, for each donor, the occupation of the donor and the name of the candidate to whom he/she donated. 3/11/2021 Slide 48

Join as a derived operator • Is it possible to derive the join operator from other operators that we have seen? That is, could you express every join query in terms of previous operators we have seen? T 1 ⋈joincond. T 2 joincond ( T 1 T 2) • Note that this is valid for every table T 1 and T 2 and every join condition “joincond”. • Thus the join operator is not one of the original five operators in the relational algebra. 3/11/2021 Slide 49

Foreign Key Joins • Almost every join used in the real world is a foreign key join, in which the join condition is "a foreign key equals the key it refers to". • That is the main reason it helps to draw a picture of a schema with arrows pointing from foreign keys to the keys they refer to; many software tools will do this automatically. • Such a diagram (which looks like but is not the same as an ER diagram) can be very helpful in formulating join queries. • That's why I gave you the file www. cs. pdx. edu/~len/386/FK. JPG to help you in homework 2. 3/11/2021 Slide 50

Seldom used Flavors of Join • The join operators we use are called equijoins since the join conditions are equalities between attributes, typically a foreign key to the key that it references. • There are 2 other kinds of joins that are seldom used. • One is inequalities between attributes, called theta-join or θ-join. Those of you who have used databases: have you ever seen one? • Here’s an example. What does it compute? commid, commid(indivcl ⋈ amount<amountindivcl) 3/11/2021 Slide 51

Natural Join • Another seldom used flavor of join (in practice, though it is important in theory) is the join operator ⋈ without any subscript, called a natural join. To make this work, you give foreign keys the same name as the key they refer to. Here’s an example, with the foreign keys in italics: newcandcl( candid, candname, party, street 1, commid) newcommcl( commid, commname, address, candid) newindivcl( fecid, commid, occup, month, amount) • The natural join newindivcl ⋈ newcommcl will combine each donation with the committee donated to. • There are four reasons the use of natural join is discouraged : 1. It does not permit the use of meaningful attribute names like candcl(princomm) or commcl(assoccand). 2. If you add a new attribute, it may break existing code. 3. Sometimes a natural join does not give what is intended. For example, what will the query newcandcl ⋈ newcommcl produce? 4. It's hard to distinguish between a natural join and a join without conditions. 3/11/2021 Slide 52

Set Operators in Relational Algebra • Set Operators (Union, difference, intersect) in relational algebra are very similar to SQL's set operators. • Their operands must be union-compatible, that is, have the same domains in corresponding attributes, though not necessarily the same names. 3/11/2021 Slide 53

The Union Operator • Suppose indivlast represents donations from 2006, and we want to form the table of 2006 and 2008 donations. • The natural operator is Union: indivcl indivlast • The Union operator, in the relational model and in DBMSs, eliminates duplicates. 3/11/2021 Slide 54

The Difference Operator * • Write the RA expression that lists the committees that did not receive donations. 3/11/2021 Slide 55

The Intersect Operator * • R intersect S, R S, is the rows that are in R and S. • Like join, intersect adds no computational power to the five basic relational algebra operators, because R S = R (R S) • What is the meaning of this query? princommcandcl commid( amount>500 indivcl) 3/11/2021 Slide 56

LO 2. 6 Practice* • What are the occupations of donors who have given at least one donation of > 500 and at least one donation of <500? • What are the IDs of Committees who have received at least one donation > 1000 and at least one donation < 250 but whose street 1 is not ‘ 228 S WASHINGTON ST’? 3/11/2021 Slide 57

The Rename Operator ρ • Our relational algebraic expressions will soon get too complex to put on one line, or to formulate in one step. • The rename operator ρ allows us to form temporary tables. ρ(temp, comm. ID ( street 1=‘ 228 S WASHINGTON ST’ commcl)) • This places the result of the query into the table named temp. 3/11/2021 Slide 58

The Divide Operator • A(x, y) B(y) is all values of x such that (x, y) is in A for every value of y in B. • What are the occupations of donors who have given to the principal committee of every democratic candidate? • First form the principal committee of every DEM candidate: ρ( B, princomm ( party='DEM' candcl)) princomm C 00431445 C 00437277 • Now form the occupations and committees of donors: ρ( A, commid, occup (indivcl)) and calculate the results A B 3/11/2021 Slide 59

Divide as a derived operator • Division is another operator that can be derived from the five basic operators, but is useful for logic applications. • Idea: For R(x, y) S(y), compute all x values that are not “disqualified” by some y value in S. • x value is disqualified if for some y value in S, (x, y) is not in X Disqualified x values: x(( x(R) S) R) R S = x (R) disqualified x values 3/11/2021 Slide 60

Division in SQL Find account owners who own all types of accounts SELECT A 1. Owner FROM Account-owner A 1 Find owners A 1 such that WHERE NOT EXISTS ( SELECT T. Type There is no account type T FROM Account-types T WHERE NOT EXISTS ( SELECT A 2. * That A 1 does not possess FROM Account-owner A 2 WHERE A 2. Type=T. Type AND A 2. Owner=A 1. Owner)) 3/11/2021 Slide 61