LECTURE 3 Single Neuron Models 1 I Overview

LECTURE 3 Single Neuron Models (1)

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

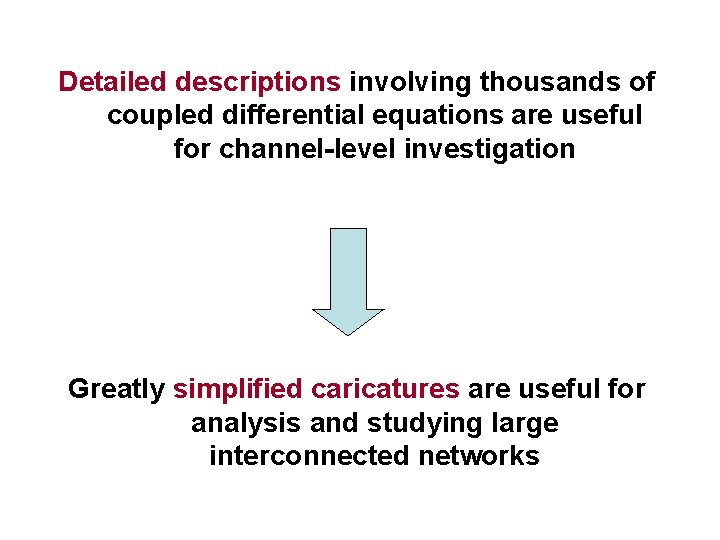
Detailed descriptions involving thousands of coupled differential equations are useful for channel-level investigation Greatly simplified caricatures are useful for analysis and studying large interconnected networks

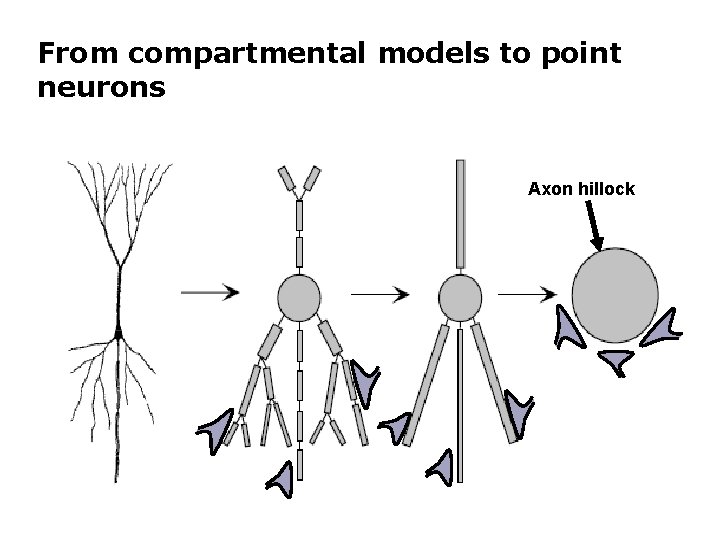
From compartmental models to point neurons Axon hillock

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

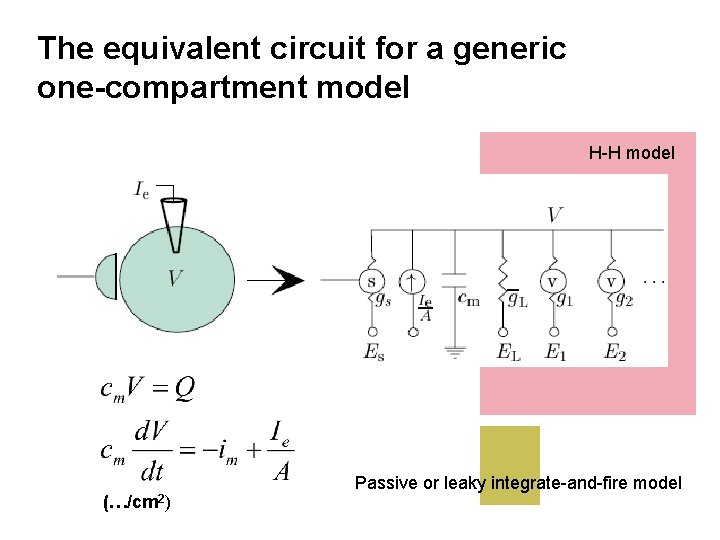
The equivalent circuit for a generic one-compartment model H-H model (…/cm 2) Passive or leaky integrate-and-fire model

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

• Maybe the most popular neural model • One of the oldest models (Lapicque 1907) (Action potentials are generated when the integrated sensory or synaptic inputs to a neuron reach a threshold value) • Although very simple, captures almost all of the important properties of the cortical neuron • Divides the dynamics of the neuron into two regimes – Sub- Threshold – Supra- Threshold

(τm = Rm. Cm = rmcm) • Sub Threshold: － Linear ODE － Without input ( at ( ) ), the stable fixed point

• Supra- Threshold: – The shape of the action potentials are more or less the same – At the synapse, the action potential events translate into transmitter release – As far as neuronal communication is concerned, the exact shape of the action potentials is not important, rather its time of occurrence is important

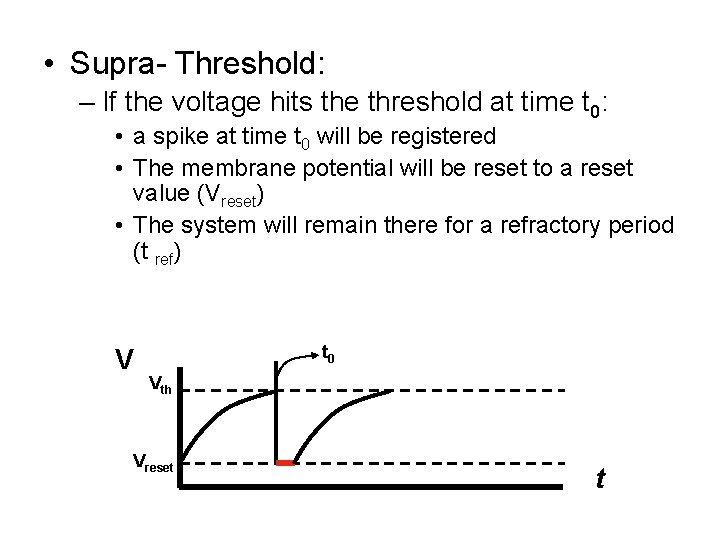
• Supra- Threshold: – If the voltage hits the threshold at time t 0: • a spike at time t 0 will be registered • The membrane potential will be reset to a reset value (Vreset) • The system will remain there for a refractory period (t ref) V t 0 Vth Vreset t

Formula summary

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

Under the assumption: The information is coded by the firing rate of the neurons and individual spikes are not important We have:

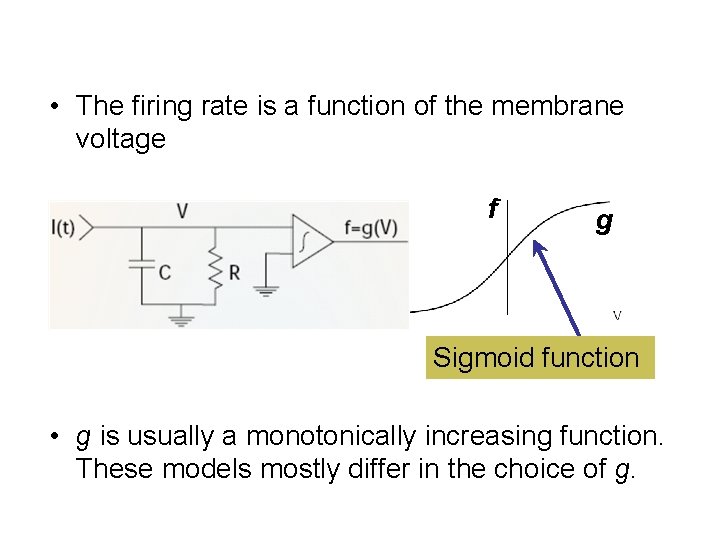
• The firing rate is a function of the membrane voltage f g Sigmoid function • g is usually a monotonically increasing function. These models mostly differ in the choice of g.

• Linear-Threshold model: f V • Based on the observation of the gain function in cortical neurons: f 100 Hz Physiological Range I

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

Nobel Prize in Physiology or Medicine in 1963 • Combination of experiments, theoretical hypotheses, data fitting and model prediction • Empirical model to describe generation of action potentials • Published in the Journal of Physiology in 1952 in a series of 5 articles (with Bernard Katz)

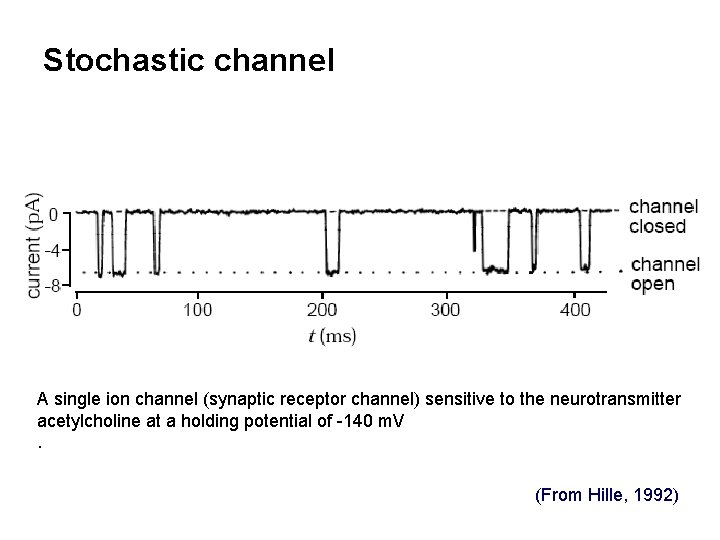
Stochastic channel A single ion channel (synaptic receptor channel) sensitive to the neurotransmitter acetylcholine at a holding potential of -140 m. V. (From Hille, 1992)

Single-channel probabilistic formulations Macroscopic deterministic descriptions

(μS/mm 2 m. S/mm 2) the conductance of an open channel × the density of channels in the membrane × the fraction of channels that are open at that time

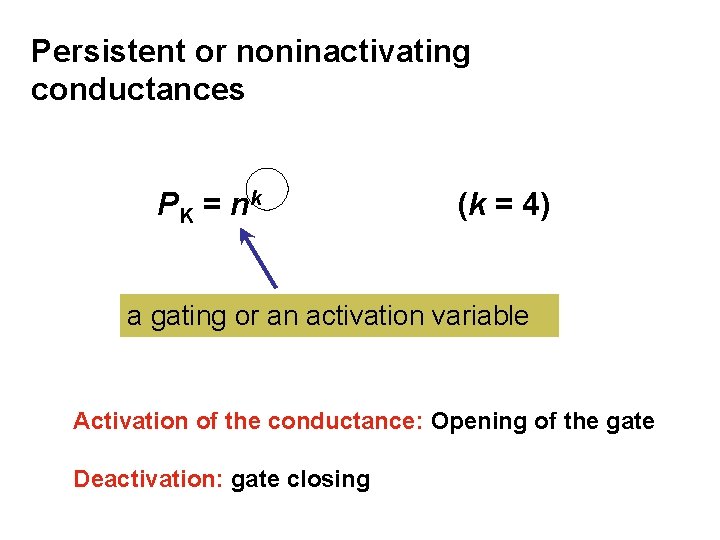
Persistent or noninactivating conductances PK = nk (k = 4) a gating or an activation variable Activation of the conductance: Opening of the gate Deactivation: gate closing

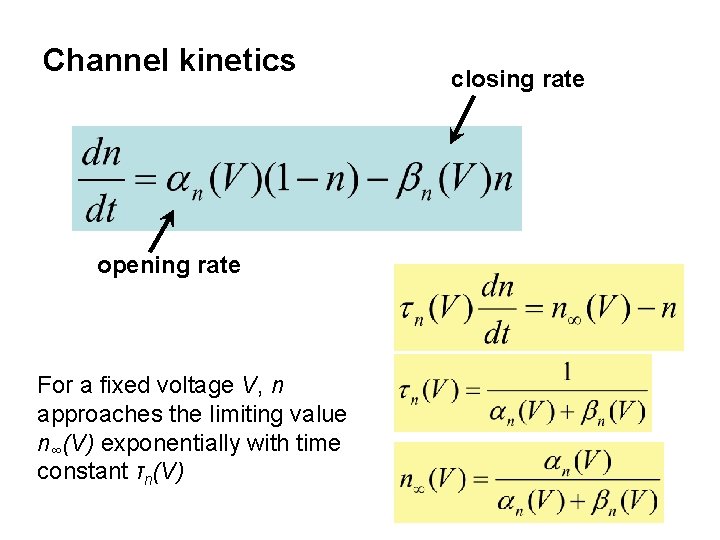
Channel kinetics opening rate For a fixed voltage V, n approaches the limiting value n∞(V) exponentially with time constant τn(V) closing rate

For the delayed-rectifier K+ conductance open n closed (1 -n)

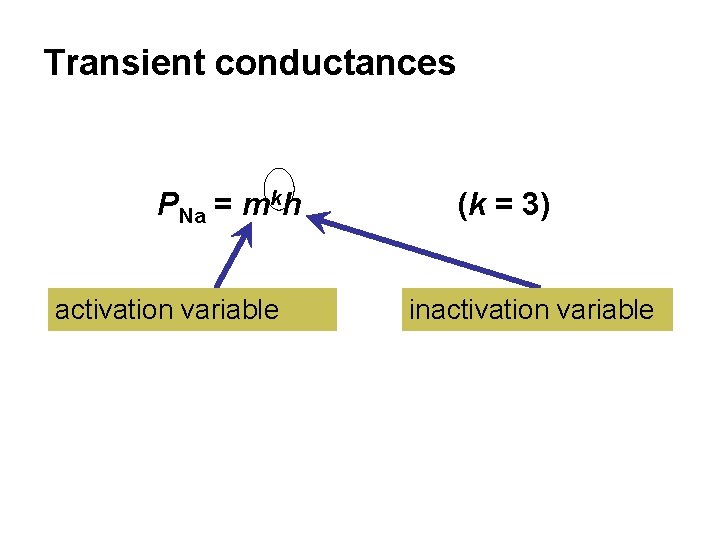
Transient conductances PNa = mkh activation variable (k = 3) inactivation variable

m or h

The Hodgkin-Huxley Model Gating equation

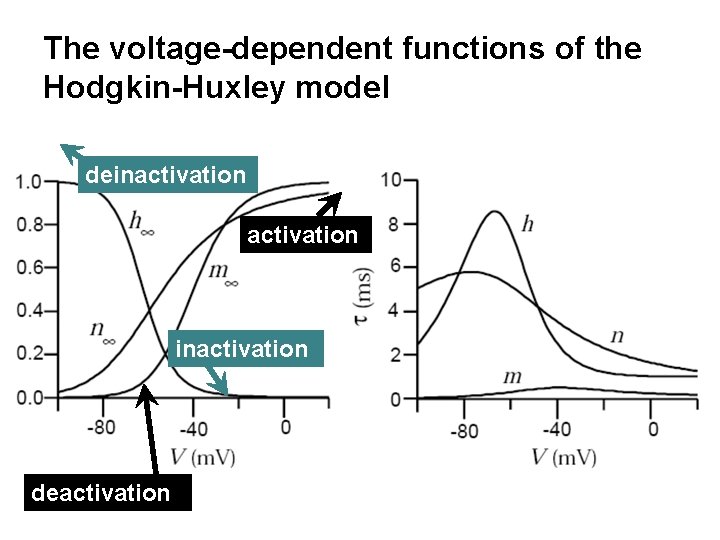
The voltage-dependent functions of the Hodgkin-Huxley model deinactivation deactivation

Improving Hodgkin-Huxley Model Connor-Stevens Model (HH + transient A-current K+) (EA~ EK) －type I behavior (continuous firing rate) transient Ca 2+ conductance (L, T, N, and P types. ECa. T = 120 m. V) － Ca 2+ spike, burst spiking, thalamic relay neurons Ca 2+-dependent K+ conductance －spike-rate adaptation

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

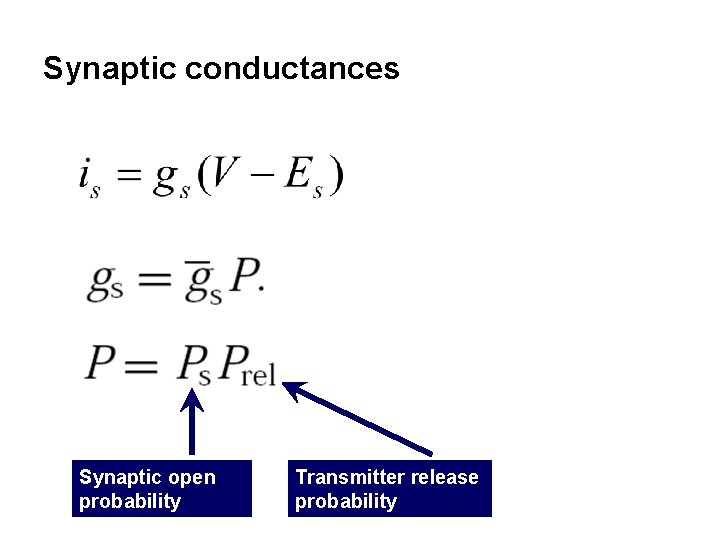
Synaptic conductances Synaptic open probability Transmitter release probability

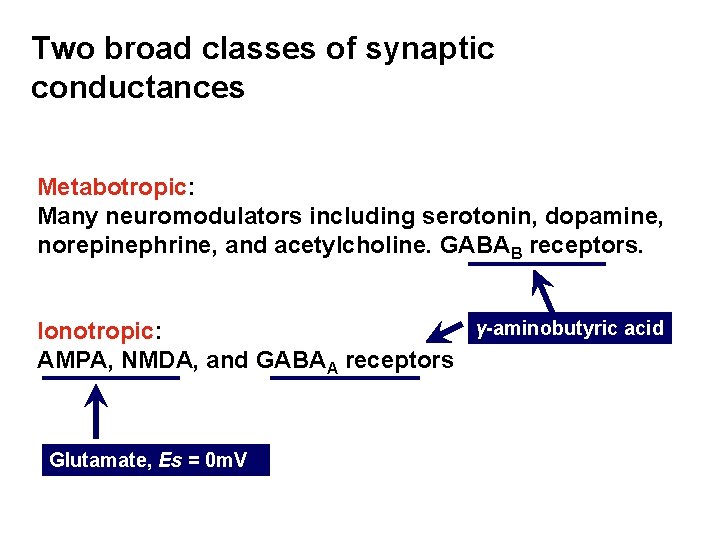
Two broad classes of synaptic conductances Metabotropic: Many neuromodulators including serotonin, dopamine, norepinephrine, and acetylcholine. GABAB receptors. γ-aminobutyric acid Ionotropic: AMPA, NMDA, and GABAA receptors Glutamate, Es = 0 m. V

Inhibitory and excitatory synapses Inhibitory synapses: reversal potentials being less than the threshold for action potential generation (GABAA , Es = -80 m. V) Excitatory synapses: those with more depolarizing reversal potentials (AMPA, NMDA, Es = 0 m. V)

The postsynaptic conductance T = 1 ms

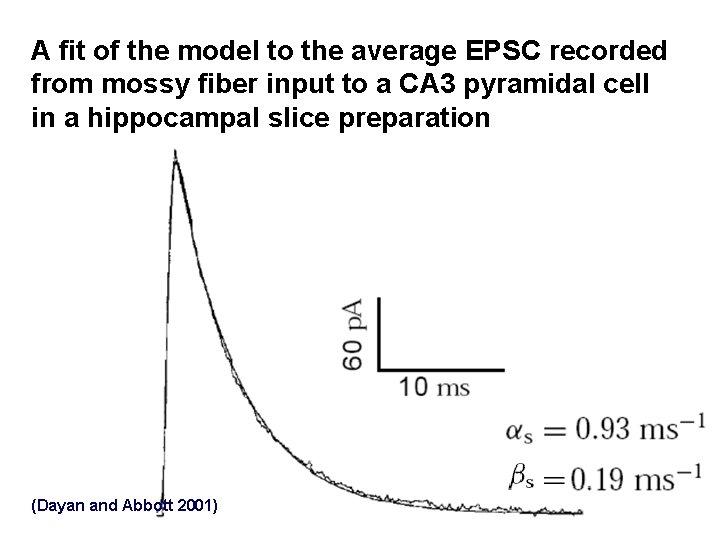
A fit of the model to the average EPSC recorded from mossy fiber input to a CA 3 pyramidal cell in a hippocampal slice preparation (Dayan and Abbott 2001)

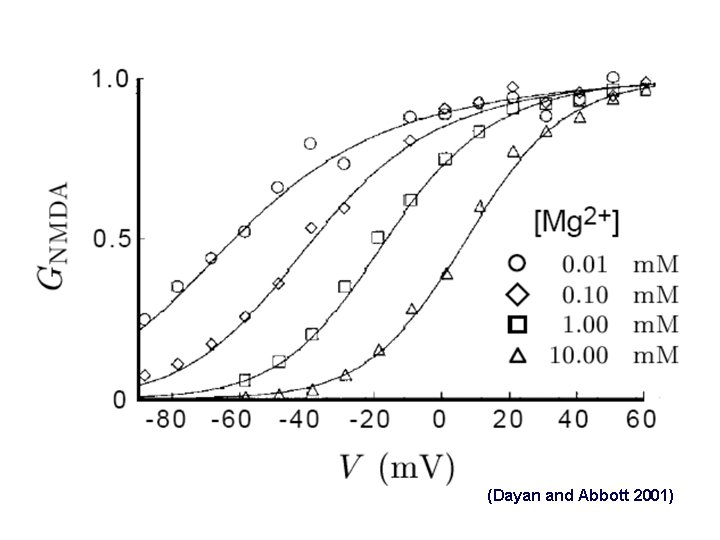
NMDA receptor conductance 1. When the postsynaptic neuron is near its resting potential, NMDA receptors are blocked by Mg 2+ ions. To activate the conductance, the postsynaptic neuron must be depolarized to knock out the blocking ions 2. The opening of NMDA receptor channels requires both pre- and postsynaptic depolarization (synaptic modification)

(Dayan and Abbott 2001)

Synapses On Integrate-and-Fire Neurons

I. Overview II. Single-Compartment Models − Integrate-and-Fire Models − Firing rate models − The Hodgkin-Huxley Model − Synaptic conductance description − The Runge-Kutta method III. Multi-Compartment Models − Two-Compartment Models

The Runge-Kutta method (simple and robust) An initial value problem: Then, the RK 4 method is given as follows: where yn + 1 is the RK 4 approximation of y(tn + 1), and

Program in Matlab or C