Lecture 3 OUTLINE Band gap energy Density of

Lecture #3 OUTLINE • Band gap energy • Density of states • Doping Read: Chapter 2 (Section 2. 3)

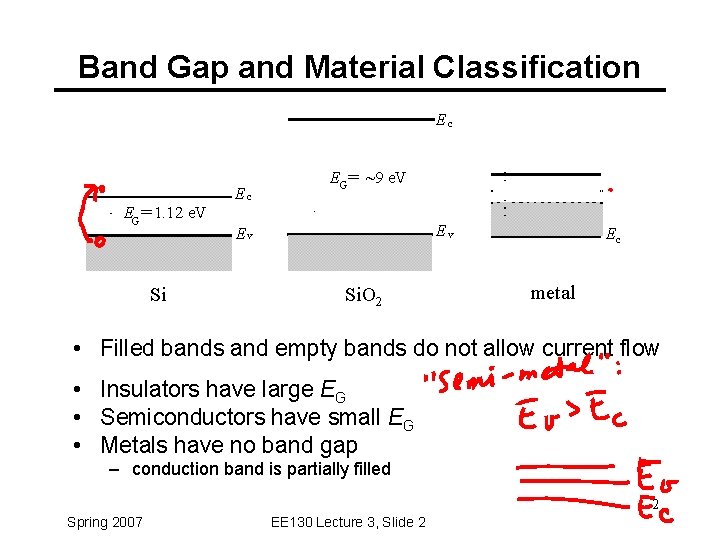
Band Gap and Material Classification Ec EG = 1. 12 e. V Si Ec EG= ~9 e. V Ev Ev Si. O 2 Ec metal • Filled bands and empty bands do not allow current flow • Insulators have large EG • Semiconductors have small EG • Metals have no band gap – conduction band is partially filled 2 Spring 2007 EE 130 Lecture 3, Slide 2

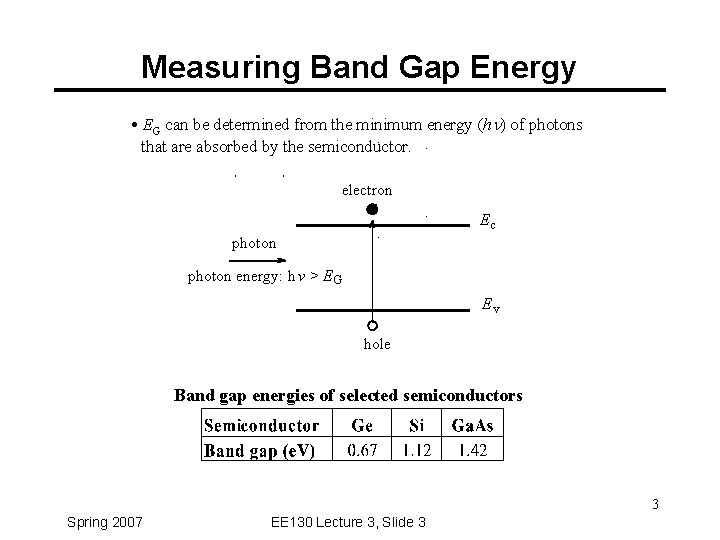
Measuring Band Gap Energy · EG can be determined from the minimum energy (hn) of photons that are absorbed by the semiconductor. electron Ec photon energy: h v > E G Ev hole Band gap energies of selected semiconductors 3 Spring 2007 EE 130 Lecture 3, Slide 3

Density of States E Ec DE Ev gc(E) Ec Ev gv(E) g(E)d. E = number of states per cm 3 in the energy range between E and E+d. E Near the band edges: E Ec E Ev 4 Spring 2007 EE 130 Lecture 3, Slide 4

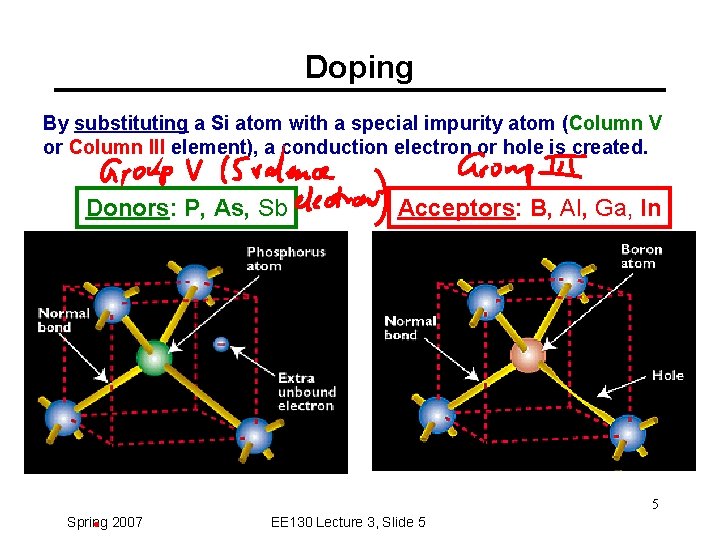
Doping By substituting a Si atom with a special impurity atom (Column V or Column III element), a conduction electron or hole is created. Donors: P, As, Sb Acceptors: B, Al, Ga, In 5 Spring 2007 EE 130 Lecture 3, Slide 5

Doping Silicon with Donors Example: Add arsenic (As) atom to the Si crystal The loosely bound 5 th valence electron of the As atom “breaks free” and becomes a mobile electron for current conduction. 6 Spring 2007 EE 130 Lecture 3, Slide 6

Doping Silicon with Acceptors Example: Add boron (B) atom to the Si crystal The B atom accepts an electron from a neighboring Si atom, resulting in a missing bonding electron, or “hole”. The hole is free to roam around the Si lattice, carrying current as a positive charge. 7 Spring 2007 EE 130 Lecture 3, Slide 7

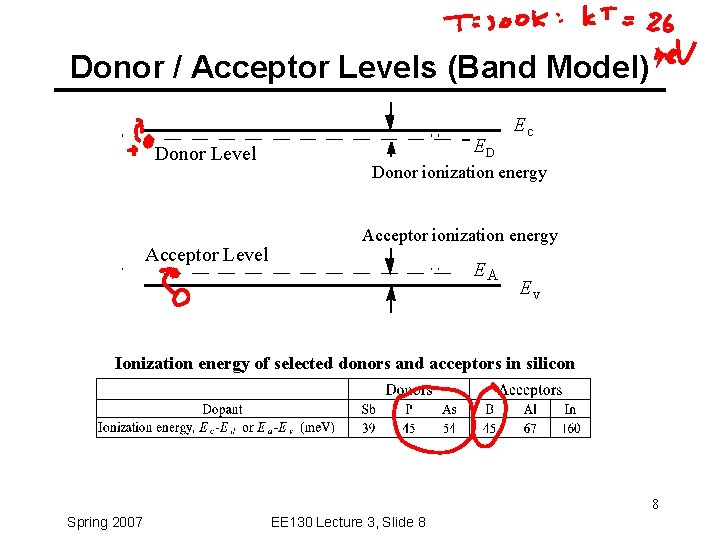
Donor / Acceptor Levels (Band Model) Donor Level Acceptor Level ED Ec Donor ionization energy Acceptor ionization energy EA Ev Ionization energy of selected donors and acceptors in silicon 8 Spring 2007 EE 130 Lecture 3, Slide 8

Charge-Carrier Concentrations ND: ionized donor concentration (cm-3) NA: ionized acceptor concentration (cm-3) Charge neutrality condition: ND + p = NA + n At thermal equilibrium, np = ni 2 (“Law of Mass Action”) Note: Carrier concentrations depend on net dopant concentration (ND - NA) ! 9 Spring 2007 EE 130 Lecture 3, Slide 9

N-type Material ND >> NA (ND – NA >> ni): 10 Spring 2007 EE 130 Lecture 3, Slide 10

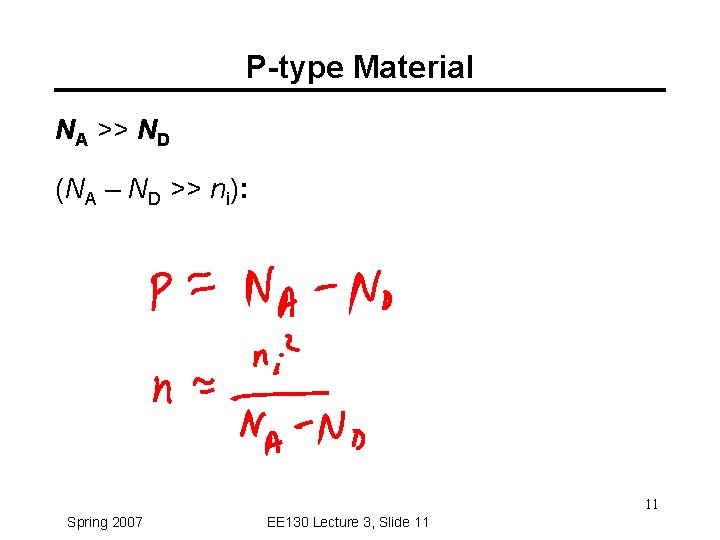
P-type Material NA >> ND (NA – ND >> ni): 11 Spring 2007 EE 130 Lecture 3, Slide 11

Terminology donor: impurity atom that increases n acceptor: impurity atom that increases p n-type material: contains more electrons than holes p-type material: contains more holes than electrons majority carrier: the most abundant carrier minority carrier: the least abundant carrier intrinsic semiconductor: n = p = ni extrinsic semiconductor: doped semiconductor 12 Spring 2007 EE 130 Lecture 3, Slide 12

Summary • The band gap energy is the energy required to free an electron from a covalent bond. – EG for Si at 300 K = 1. 12 e. V – Insulators have large EG; semiconductors have small EG • Dopants in Si: – Reside on lattice sites (substituting for Si) – Group-V elements contribute conduction electrons, and are called donors – Group-III elements contribute holes, and are called acceptors – Very low ionization energies (<50 me. V) ionized at room temperature Dopant concentrations typically range from 1014 cm 13 -3 20 cm-3 Spring EE 130 Lecture 3, Slide 13 to 102007