Lecture 3 Modeling ii State Space approach 3









- Slides: 19

Lecture 3 Modeling (ii) –State Space approach 3. 1 State Variables of a Dynamical System 3. 2 State Variable Equation 3. 3 Why State space approach 3. 4 Derive Transfer Function from State Space Equation 3. 5 Time Response and State Transition Matrix Modern Control Systems

State equation Dynamic equation Output equation State variable State space r- input p- output Modern Control Systems 2

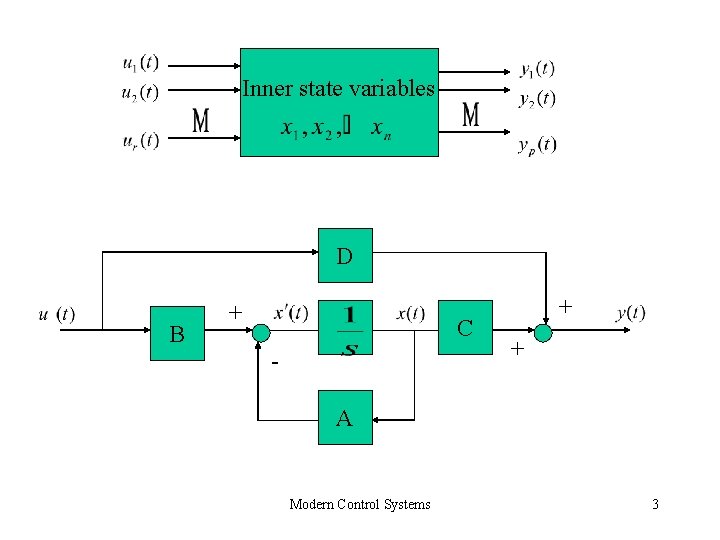
Inner state variables D B + C - + + A Modern Control Systems 3

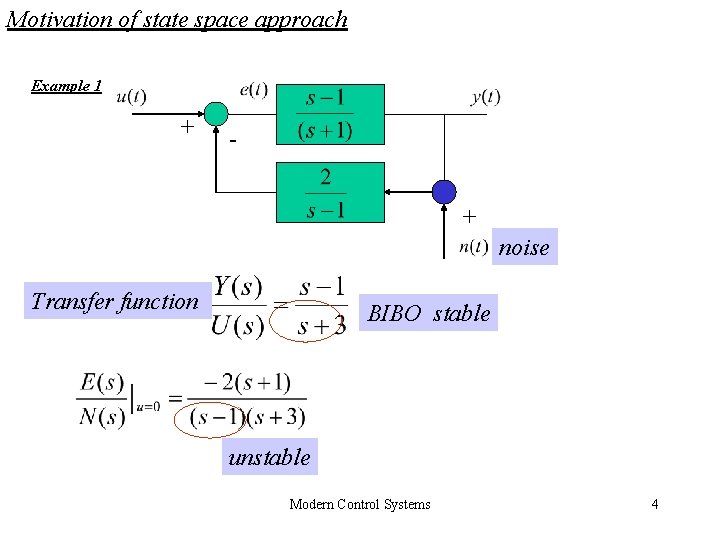
Motivation of state space approach Example 1 + + noise Transfer function BIBO stable unstable Modern Control Systems 4

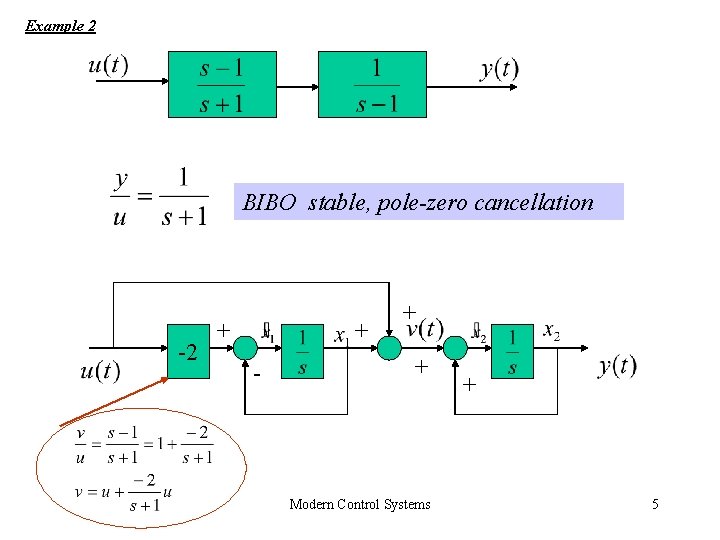
Example 2 BIBO stable, pole-zero cancellation -2 + + - + + Modern Control Systems + 5

then system stable State-space description Internal behavior description Modern Control Systems 6

Definition: The state of a system at time information at that together with uniquely the behavior of the system for is the amount of determines Example M 單純從 並無法決定x在 以後的運動狀 況。除非知道 與 。所以 與 是這個系統過去的歷史總結。故 與 可 以作為系統的狀態。 Modern Control Systems 7

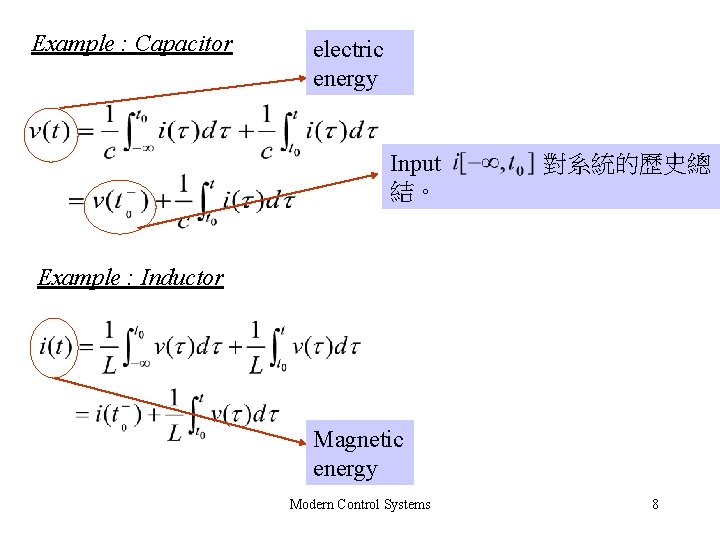
Example : Capacitor electric energy Input 結。 對系統的歷史總 Example : Inductor Magnetic energy Modern Control Systems 8

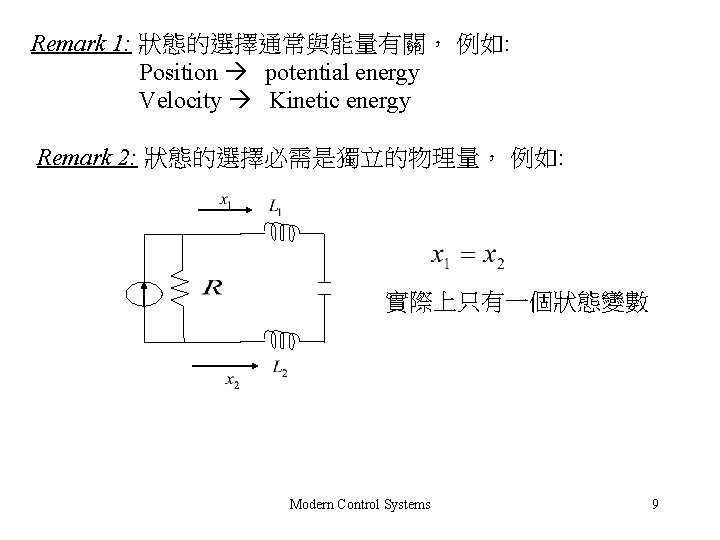
Remark 1: 狀態的選擇通常與能量有關, 例如: Position potential energy Velocity Kinetic energy Remark 2: 狀態的選擇必需是獨立的物理量, 例如: 實際上只有一個狀態變數 Modern Control Systems 9

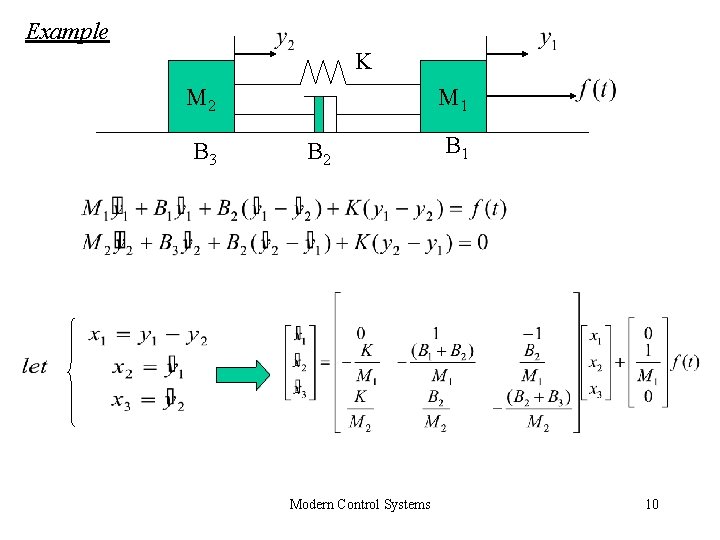
Example K M 2 B 3 M 1 B 2 Modern Control Systems B 1 10

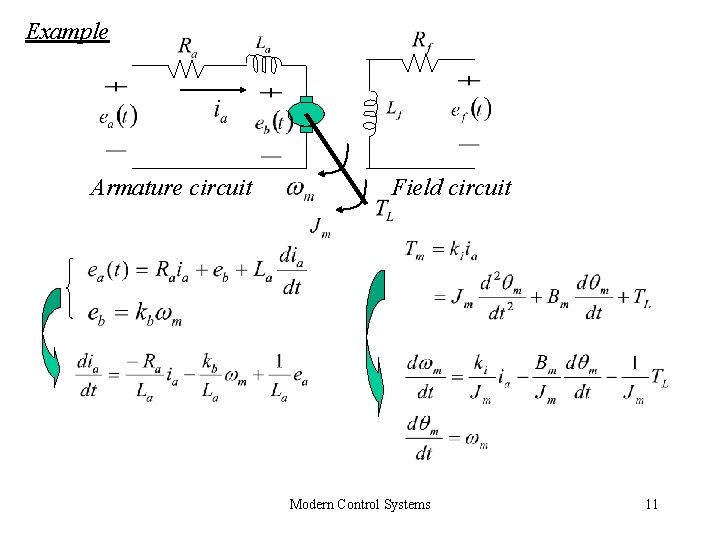
Example Armature circuit Field circuit Modern Control Systems 11

Modern Control Systems 12

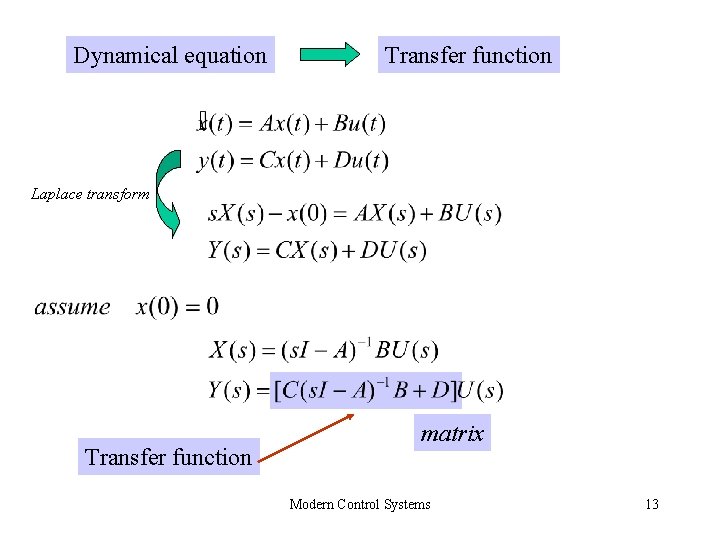
Dynamical equation Transfer function Laplace transform Transfer function matrix Modern Control Systems 13

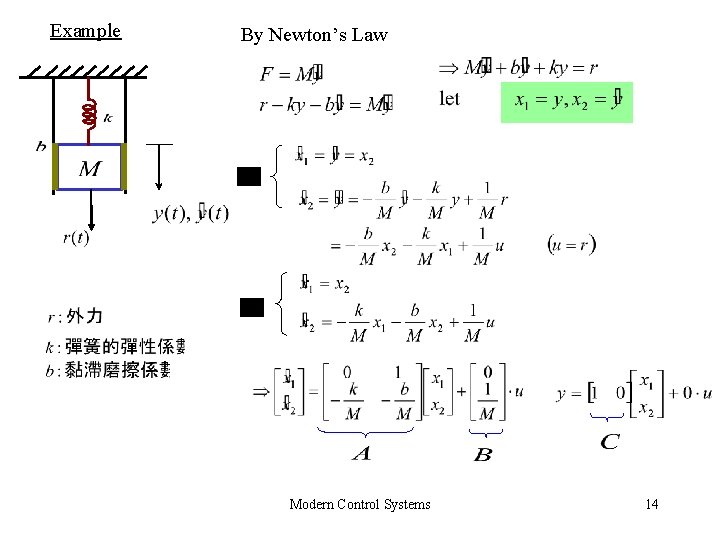
Example By Newton’s Law Modern Control Systems 14

State Space Equation Transfer Function Example: Transfer function of the Mass-damper-spring system Modern Control Systems 15

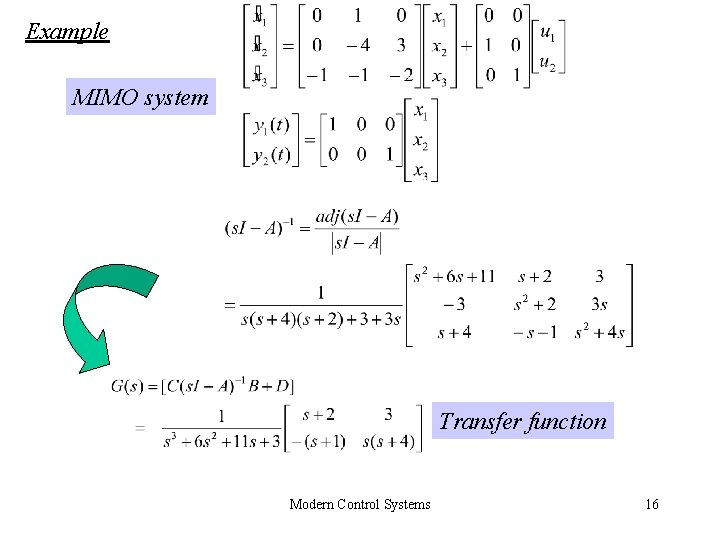
Example MIMO system Transfer function Modern Control Systems 16

Remark : the choice of states is not unique. + + - - exist a mapping Modern Control Systems 17

Different state equation description p is nonsingular Modern Control Systems 18

Definition : Two dynamical systems & with are said to be equivalent. The nonsingular matrix p is called an equivalence transformation. Theorem: two equivalent dynamical system have the same transfer function. Modern Control Systems 19