Lecture 3 Marginal Analysis for Optimal Decision Mc

Lecture 3: Marginal Analysis for Optimal Decision Mc. Graw-Hill/Irwin Copyright © 2011 by the Mc. Graw-Hill Companies, Inc. All rights reserved.

Optimization • An optimization problem involves the specification of three things: • Objective function to be maximized or minimized • Activities or choice variables that determine the value of the objective function • Any constraints that may restrict the values of the choice variables 3 -2

Optimization • Maximization problem • An optimization problem that involves maximizing the objective function • Minimization problem • An optimization problem that involves minimizing the objective function 3 -3

Optimization • Unconstrained optimization • An optimization problem in which the decision maker can choose the level of activity from an unrestricted set of values • Constrained optimization • An optimization problem in which the decision maker chooses values for the choice variables from a restricted set of values 3 -4

Choice Variables • Choice variables determine the value of the objective function • Continuous variables • Discrete variables 3 -5

Choice Variables • Continuous variables • Can choose from uninterrupted span of variables • Discrete variables • Must choose from a span of variables that is interrupted by gaps 3 -6

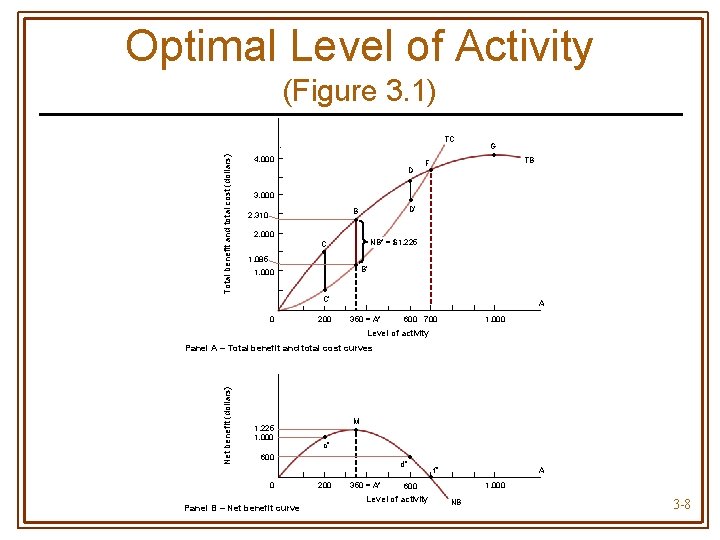
Net Benefit • Net Benefit (NB) • Difference between total benefit (TB) and total cost (TC) for the activity • NB = TB – TC • Optimal level of the activity (A*) is the level that maximizes net benefit 3 -7

Optimal Level of Activity (Figure 3. 1) Total benefit and total cost (dollars) TC 4, 000 D • • D’ 3, 000 B 2, 310 • 2, 000 1, 085 1, 000 • F • • B’ • C’ 0 200 TB NB* = $1, 225 C • G A 350 = A* 600 700 1, 000 Level of activity Net benefit (dollars) Panel A – Total benefit and total cost curves 1, 225 1, 000 M • c’’ • • 600 0 Panel B – Net benefit curve d’’ 200 350 = A* 600 A f’’ • Level of activity 1, 000 NB 3 -8

Marginal Benefit & Marginal Cost • Marginal benefit (MB) • Change in total benefit (TB) caused by an incremental change in the level of the activity • Marginal cost (MC) • Change in total cost (TC) caused by an incremental change in the level of the activity 3 -9

Marginal Benefit & Marginal Cost 3 -10

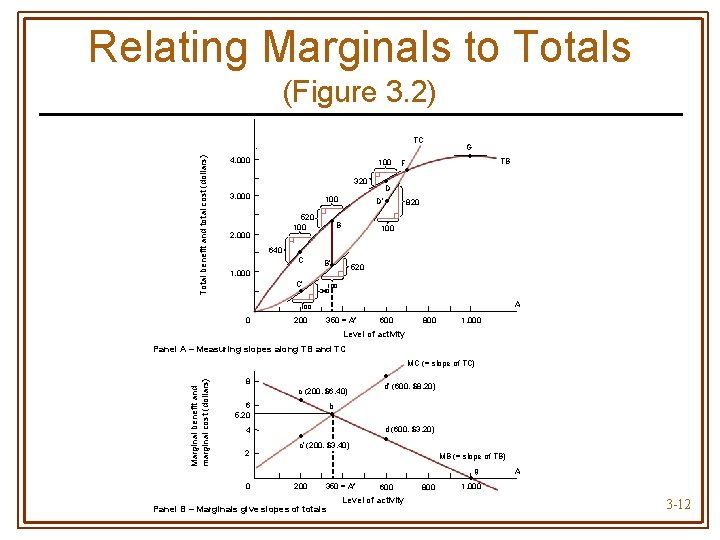
Relating Marginals to Totals • Marginal variables measure rates of change in corresponding total variables • Marginal benefit & marginal cost are also slopes of total benefit & total cost curves, respectively 3 -11

Relating Marginals to Totals (Figure 3. 2) Total benefit and total cost (dollars) TC 4, 000 100 320 3, 000 100 • B 520 100 2, 000 640 • C C’ • • F • TB 820 100 • B’ 1, 000 • D D’ • G 520 100 340 A 100 0 200 350 = A* 600 800 1, 000 Level of activity Panel A – Measuring slopes along TB and TC Marginal benefit and marginal cost (dollars) MC (= slope of TC) 8 c (200, $6. 40) 6 5. 20 4 2 • • d’ (600, $8. 20) b • • c’ (200, $3. 40) d (600, $3. 20) • MB (= slope of TB) g 0 200 350 = A* Panel B – Marginals give slopes of totals 600 Level of activity 800 • 1, 000 A 3 -12

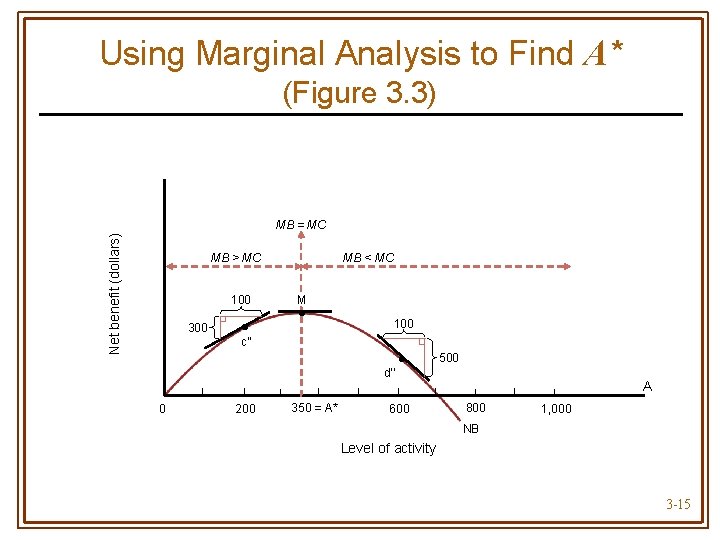
Using Marginal Analysis to Find Optimal Activity Levels • If marginal benefit > marginal cost • Activity should be increased to reach highest net benefit • If marginal cost > marginal benefit • Activity should be decreased to reach highest net benefit 3 -13

Using Marginal Analysis to Find Optimal Activity Levels • Optimal level of activity • When no further increases in net benefit are possible • Occurs when MB = MC 3 -14

Using Marginal Analysis to Find A* (Figure 3. 3) Net benefit (dollars) MB = MC MB > MC 100 300 0 • c’’ 200 MB < MC M • 100 • d’’ 350 = A* 600 500 A 800 1, 000 NB Level of activity 3 -15

Unconstrained Maximization with Discrete Choice Variables • Increase activity if MB > MC • Decrease activity if MB < MC • Optimal level of activity • Last level for which MB exceeds MC 3 -16

Irrelevance of Sunk, Fixed, and Average Costs • Sunk costs • Previously paid & cannot be recovered • Fixed costs • Constant & must be paid no matter the level of activity • Average (or unit) costs • Computed by dividing total cost by the number of units of the activity 3 -17

Irrelevance of Sunk, Fixed, and Average Costs • These costs do not affect marginal cost & are irrelevant for optimal decisions 3 -18

Constrained Optimization • The ratio MB/P represents the additional benefit per additional dollar spent on the activity • Ratios of marginal benefits to prices of various activities are used to allocate a fixed number of dollars among activities 3 -19

Constrained Optimization • To maximize or minimize an objective function subject to a constraint • Ratios of the marginal benefit to price must be equal for all activities • Constraint must be met 3 -20