Lecture 3 Linear Programming 6 S and Transportation

Lecture 3 Linear Programming (6 S) and Transportation Problem (8 S) 1

Linear Programming George Dantzig – 1914 -2005 · Concerned with optimal allocation of limited resources such as · Materials · Budgets · Labor · Machine time · among competitive activities · under a set of constraints · George Dantzig – 1914 -2005 2

Linear Programming Example Variables Maximize 60 X 1 + 50 X 2 Subject to Objective function 4 X 1 + 10 X 2 <= 100 2 X 1 + 1 X 2 <= 22 Constraints 3 X 1 + 3 X 2 <= 39 Non-negativity Constraints X 1, X 2 >= 0 What is a Linear Program? • A LP is an optimization model that has • continuous variables • a single linear objective function, and • (almost always) several constraints (linear equalities or inequalities) 3

Linear Programming Model · Decision variables · · · Objective Function · · · unknowns, which is what model seeks to determine for example, amounts of either inputs or outputs goal, determines value of best (optimum) solution among all feasible (satisfy constraints) values of the variables either maximization or minimization Constraints · · restrictions, which limit variables of the model limitations that restrict the available alternatives Parameters: numerical values (for example, RHS of constraints) · Feasible solution: is one particular set of values of the decision · variables that satisfies the constraints · · Feasible solution space: the set of all feasible solutions Optimal solution: is a feasible solution that maximizes or minimizes the objective function · There could be multiple optimal solutions 4

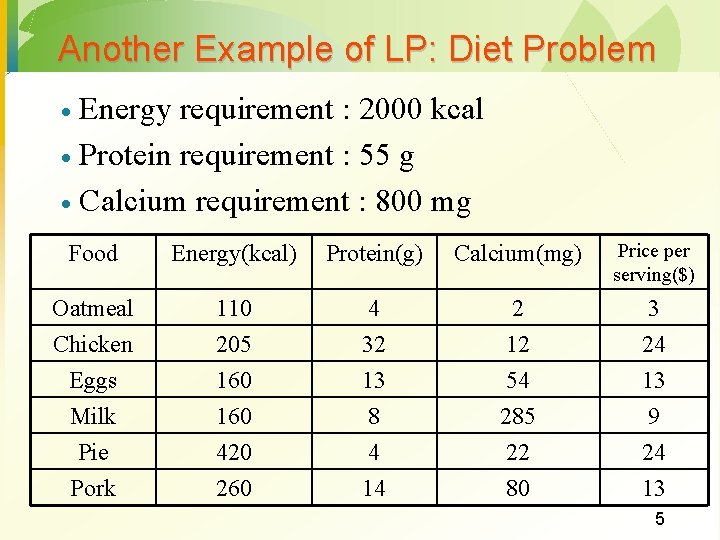
Another Example of LP: Diet Problem Energy requirement : 2000 kcal · Protein requirement : 55 g · Calcium requirement : 800 mg · Food Energy(kcal) Protein(g) Calcium(mg) Price per serving($) Oatmeal Chicken Eggs Milk Pie 110 205 160 420 4 32 13 8 4 2 12 54 285 22 3 24 13 9 24 Pork 260 14 80 13 5

Example of LP : Diet Problem oatmeal: at most 4 servings/day · chicken: at most 3 servings/day · eggs: at most 2 servings/day · milk: at most 8 servings/day · pie: at most 2 servings/day · pork: at most 2 servings/day · Design an optimal diet plan which minimizes the cost per day 6

Step 1: define decision variables · · · x 1 = # of oatmeal servings x 2 = # of chicken servings x 3 = # of eggs servings x 4 = # of milk servings x 5 = # of pie servings x 6 = # of pork servings Step 2: formulate objective function • In this case, minimize total cost minimize z = 3 x 1 + 24 x 2 + 13 x 3 + 9 x 4 + 24 x 5 + 13 x 6 7

Step 3: Constraints · Meet energy requirement 110 x 1 + 205 x 2 + 160 x 3 + 160 x 4 + 420 x 5 + 260 x 6 2000 · Meet protein requirement 4 x 1 + 32 x 2 + 13 x 3 + 8 x 4 + 4 x 5 + 14 x 6 55 · Meet calcium requirement 2 x 1 + 12 x 2 + 54 x 3 + 285 x 4 + 22 x 5 + 80 x 6 800 · Restriction on number of servings 0 x 1 4, 0 x 2 3, 0 x 3 2, 0 x 4 8, 0 x 5 2, 0 x 6 2 8

So, how does a LP look like? minimize 3 x 1 + 24 x 2 + 13 x 3 + 9 x 4 + 24 x 5 + 13 x 6 subject to 110 x 1 + 205 x 2 + 160 x 3 + 160 x 4 + 420 x 5 + 260 x 6 2000 4 x 1 + 32 x 2 + 13 x 3 + 8 x 4 + 4 x 5 + 14 x 6 55 2 x 1 + 12 x 2 + 54 x 3 + 285 x 4 + 22 x 5 + 80 x 6 800 0 x 1 4 0 x 2 3 0 x 3 2 0 x 4 8 0 x 5 2 0 x 6 2 9

Guidelines for Model Formulation Understand the problem thoroughly. · Describe the objective. · Describe each constraint. · Define the decision variables. · Write the objective in terms of the decision variables. · Write the constraints in terms of the decision variables · · Do not forget non-negativity constraints 10

Transportation Problem · Objective: · · · determination of a transportation plan of a single commodity from a number of sources to a number of destinations, such that total cost of transportation is minimized Sources may be plants, destinations may be warehouses Question: · · · how many units to transport from source i to destination j such that supply and demand constraints are met, and total transportation cost is minimized 11

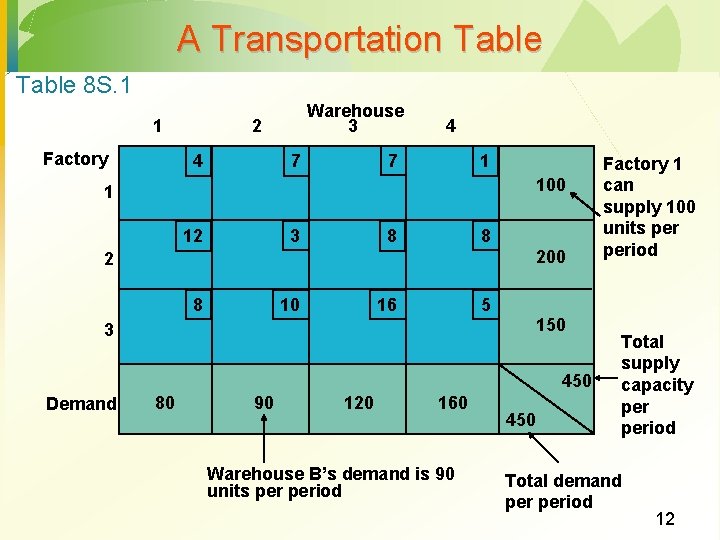
A Transportation Table 8 S. 1 1 Factory Warehouse 3 2 4 4 7 7 1 100 1 3 12 8 8 200 2 10 8 16 5 150 3 450 Demand 80 90 120 Factory 1 can supply 100 units period 160 Warehouse B’s demand is 90 units period 450 Total supply capacity period Total demand period 12

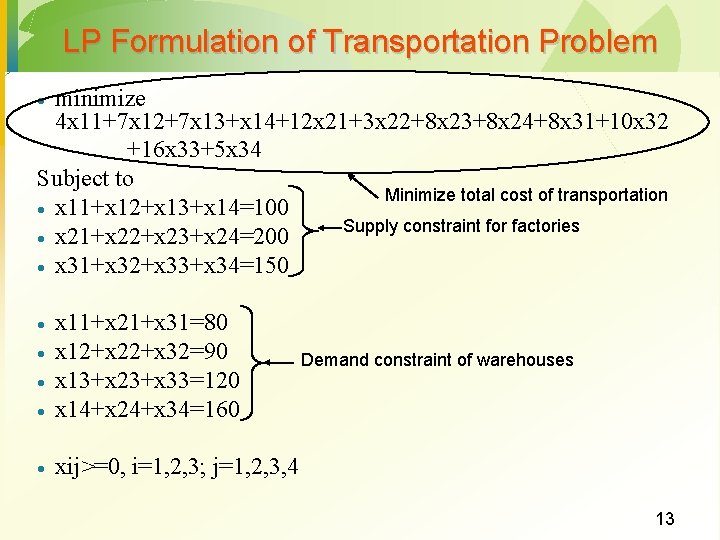
LP Formulation of Transportation Problem minimize 4 x 11+7 x 12+7 x 13+x 14+12 x 21+3 x 22+8 x 23+8 x 24+8 x 31+10 x 32 +16 x 33+5 x 34 Subject to Minimize total cost of transportation · x 11+x 12+x 13+x 14=100 Supply constraint for factories · x 21+x 22+x 23+x 24=200 · x 31+x 32+x 33+x 34=150 · · x 11+x 21+x 31=80 x 12+x 22+x 32=90 x 13+x 23+x 33=120 x 14+x 24+x 34=160 · xij>=0, i=1, 2, 3; j=1, 2, 3, 4 · · · Demand constraint of warehouses 13

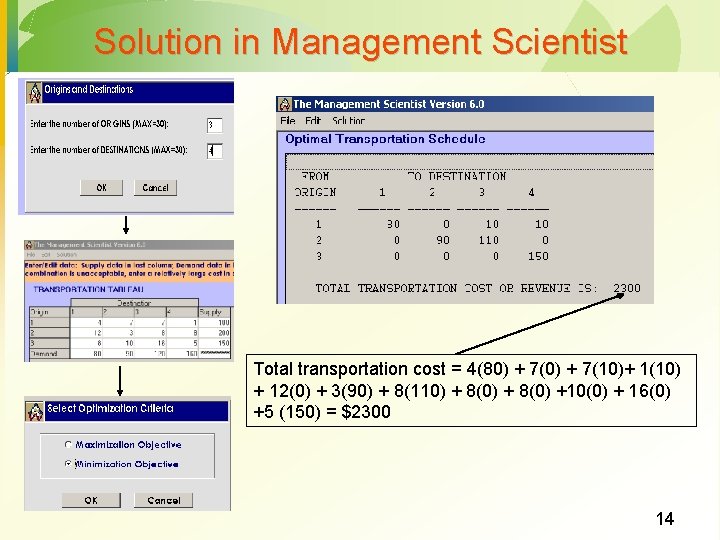
Solution in Management Scientist Total transportation cost = 4(80) + 7(10)+ 1(10) + 12(0) + 3(90) + 8(110) + 8(0) +10(0) + 16(0) +5 (150) = $2300 14

Assignment Problem · Special case of transportation problem When # of rows = # of columns in the transportation tableau · All supply and demands =1 · Objective: Assign n jobs/workers to n machines such that the total cost of assignment is minimized · Plenty of practical applications · Job shops · Hospitals · Airlines, etc. · 15

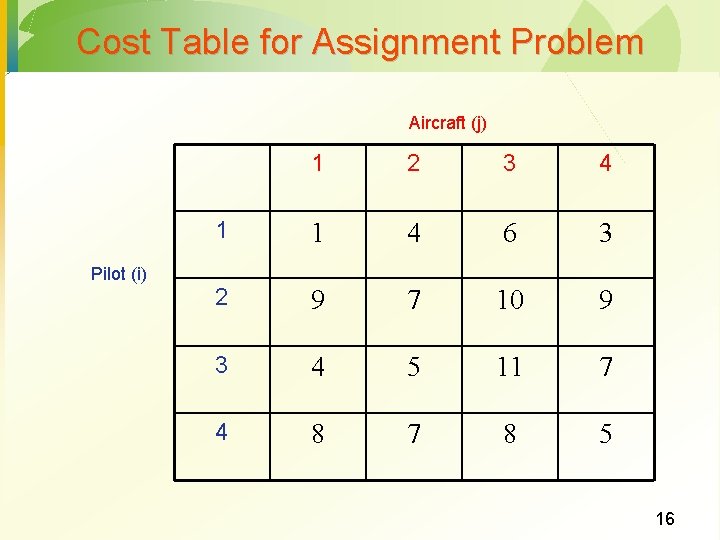
Cost Table for Assignment Problem Aircraft (j) Pilot (i) 1 2 3 4 1 1 4 6 3 2 9 7 10 9 3 4 5 11 7 4 8 7 8 5 16

LP Formulation of Assignment Problem minimize x 11+4 x 12+6 x 13+3 x 14 + 9 x 21+7 x 22+10 x 23+9 x 24 + 4 x 31+5 x 32+11 x 33+7 x 34 + 8 x 41+7 x 42+8 x 43+5 x 44 subject to · x 11+x 12+x 13+x 14=1 · x 21+x 22+x 23+x 24=1 · x 31+x 32+x 33+x 34=1 · x 41+x 42+x 43+x 44=1 · · · x 11+x 21+x 31+x 41=1 x 12+x 22+x 32+x 42=1 x 13+x 23+x 33+x 43=1 x 14+x 24+x 34+x 44=1 xij = 1, if pilot i is assigned to aircraft j, i=1, 2, 3, 4; j=1, 2, 3, 4 0 otherwise 17

Product Mix Problem • • • Floataway Tours has $420, 000 that can be used to purchase new rental boats for hire during the summer. The boats can be purchased from two different manufacturers. Floataway Tours would like to purchase at least 50 boats. They would also like to purchase the same number from Sleekboat as from Racer to maintain goodwill. At the same time, Floataway Tours wishes to have a total seating capacity of at least 200. Formulate this problem as a linear program 18

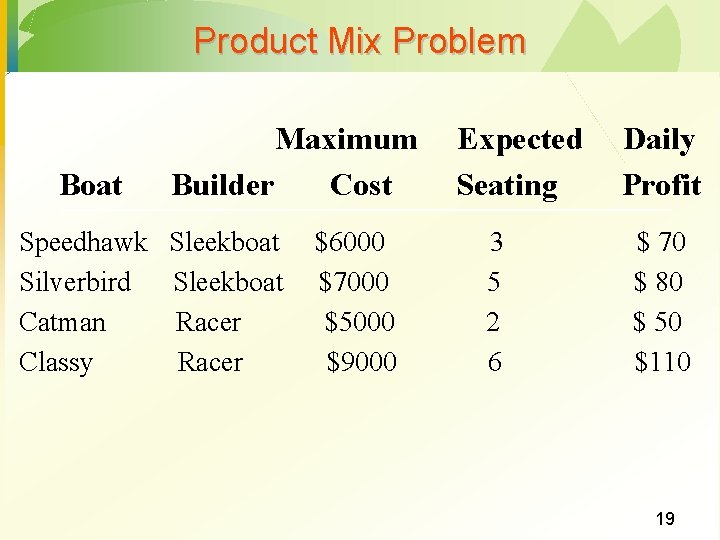
Product Mix Problem Boat Maximum Builder Cost Speedhawk Sleekboat Silverbird Sleekboat Catman Racer Classy Racer $6000 $7000 $5000 $9000 Expected Seating 3 5 2 6 Daily Profit $ 70 $ 80 $ 50 $110 19

Product Mix Problem Define the decision variables x 1 = number of Speedhawks ordered x 2 = number of Silverbirds ordered x 3 = number of Catmans ordered x 4 = number of Classys ordered · Define the objective function Maximize total expected daily profit: Max: (Expected daily profit per unit) x (Number of units) Max: 70 x 1 + 80 x 2 + 50 x 3 + 110 x 4 · 20

Product Mix Problem · Define the constraints (1) Spend no more than $420, 000: 6000 x 1 + 7000 x 2 + 5000 x 3 + 9000 x 4 < 420, 000 (2) Purchase at least 50 boats: x 1 + x 2 + x 3 + x 4 > 50 (3) Number of boats from Sleekboat equals number of boats from Racer: x 1 + x 2 = x 3 + x 4 or x 1 + x 2 - x 3 - x 4 = 0 (4) Capacity at least 200: 3 x 1 + 5 x 2 + 2 x 3 + 6 x 4 > 200 Nonnegativity of variables: xj > 0, for j = 1, 2, 3, 4 21

Product Mix Problem - Complete Formulation Max 70 x 1 + 80 x 2 + 50 x 3 + 110 x 4 s. t. 6000 x 1 + 7000 x 2 + 5000 x 3 + 9000 x 4 < 420, 000 x 1 + x 2 + x 3 + x 4 > 50 x 1 + x 2 - x 3 - x 4 = 0 3 x 1 + 5 x 2 + 2 x 3 + 6 x 4 > 200 x 1, x 2, x 3, x 4 > 0 22

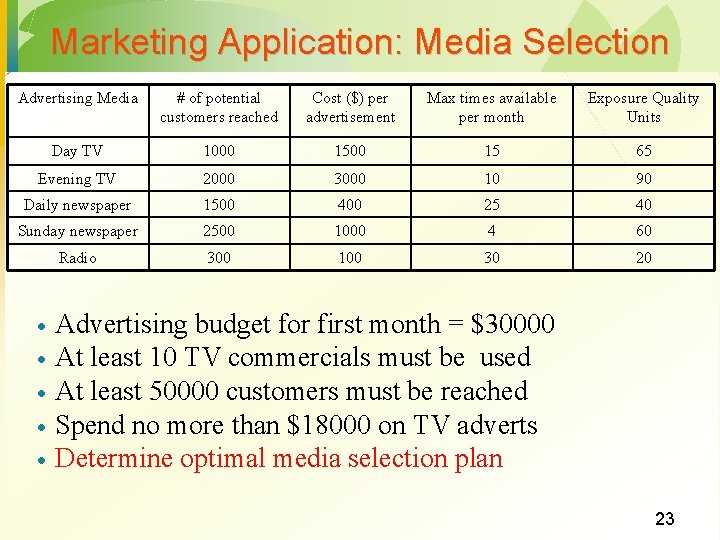
Marketing Application: Media Selection Advertising Media # of potential customers reached Cost ($) per advertisement Max times available per month Exposure Quality Units Day TV 1000 15 65 Evening TV 2000 3000 10 90 Daily newspaper 1500 400 25 40 Sunday newspaper 2500 1000 4 60 Radio 300 100 30 20 · · · Advertising budget for first month = $30000 At least 10 TV commercials must be used At least 50000 customers must be reached Spend no more than $18000 on TV adverts Determine optimal media selection plan 23

Media Selection Formulation · Step 1: Define decision variables · · · Step 2: Write the objective in terms of the decision variables · · DTV = # of day time TV adverts ETV = # of evening TV adverts DN = # of daily newspaper adverts SN = # of Sunday newspaper adverts R = # of radio adverts Maximize 65 DTV+90 ETV+40 DN+60 SN+20 R Step 3: Write the constraints in terms of the decision variables DTV ETV DN SN R + 25 <= 4 <= 30000 Availability of Media Budget + ETV >= 10 1500 DTV + 3000 ETV <= 18000 TV Constraints 1000 DTV + 2000 ETV >= 50000 Customers reached DTV, ETV, DN, SN, R >= 0 + 100 R <= DTV 2500 SN + 10 3000 ETV + 1000 SN <= + 1500 DN + 15 1500 DTV + 400 DN <= 300 R 24

Applications of LP Product mix planning · Distribution networks · Truck routing · Staff scheduling · Financial portfolios · Capacity planning · Media selection: marketing · 25

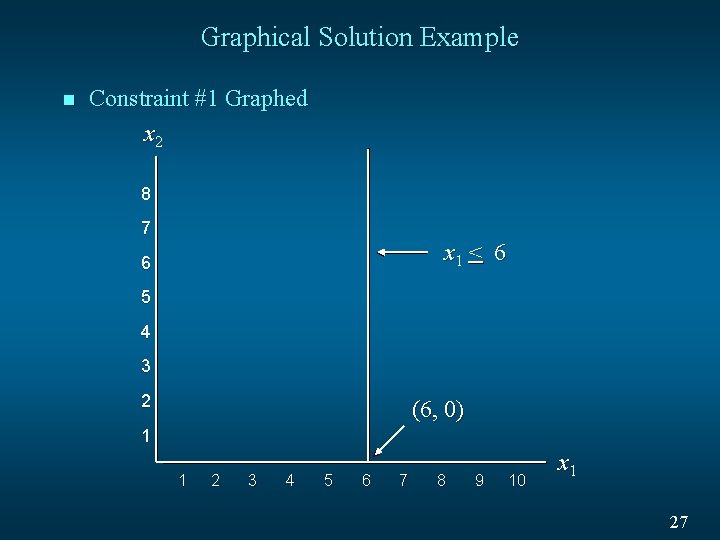
Graphical Solution of LPs · Consider a Maximization Problem Max s. t. 5 x 1 + 7 x 2 x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1, x 2 > 0 26

Graphical Solution Example n Constraint #1 Graphed x 2 8 7 x 1 < 6 6 5 4 3 2 (6, 0) 1 1 2 3 4 5 6 7 8 9 10 x 1 27

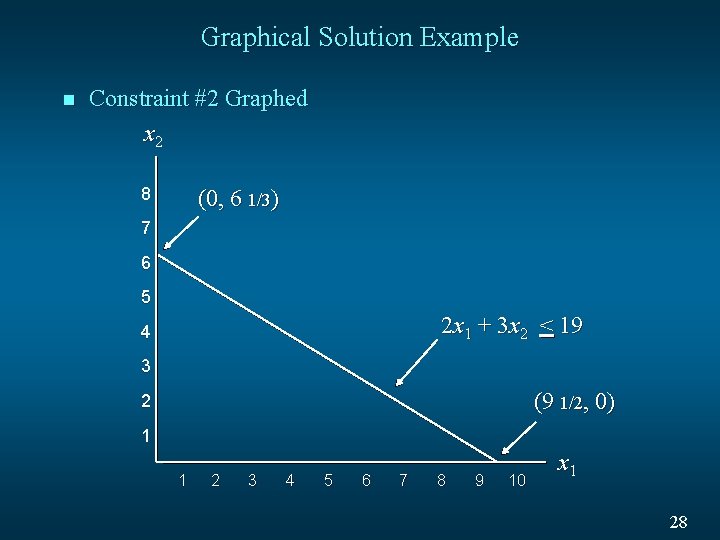
Graphical Solution Example n Constraint #2 Graphed x 2 8 (0, 6 1/3) 7 6 5 2 x 1 + 3 x 2 < 19 4 3 (9 1/2, 0) 2 1 1 2 3 4 5 6 7 8 9 10 x 1 28

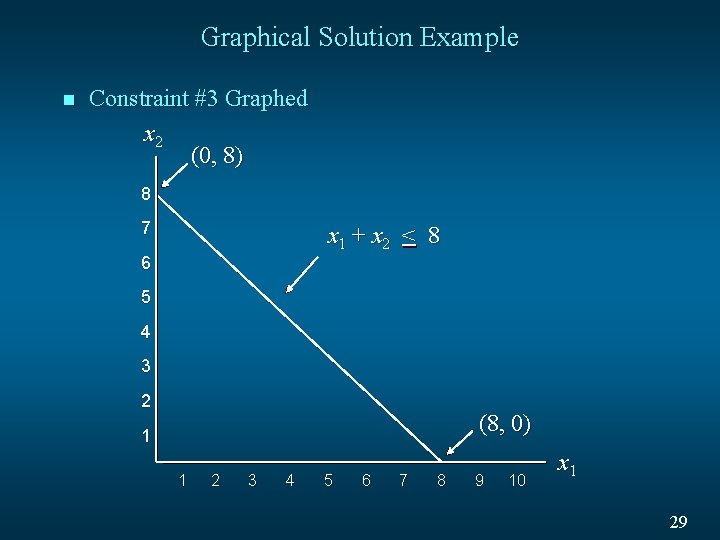
Graphical Solution Example n Constraint #3 Graphed x 2 (0, 8) 8 7 x 1 + x 2 < 8 6 5 4 3 2 (8, 0) 1 1 2 3 4 5 6 7 8 9 10 x 1 29

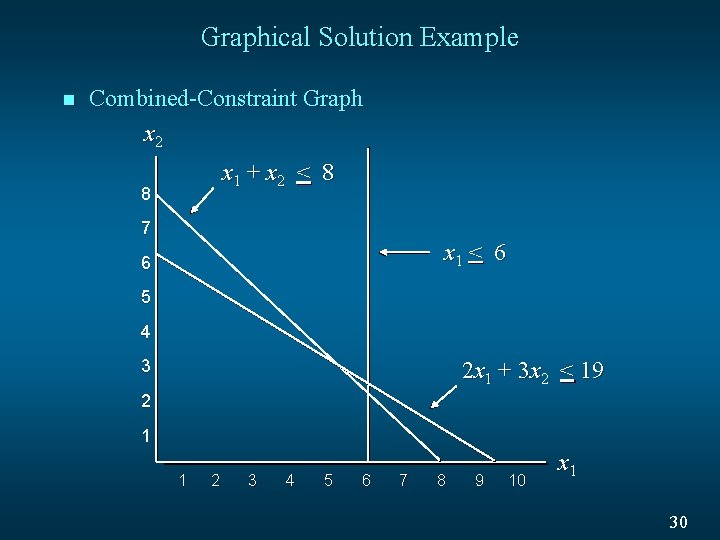
Graphical Solution Example n Combined-Constraint Graph x 2 x 1 + x 2 < 8 8 7 x 1 < 6 6 5 4 3 2 x 1 + 3 x 2 < 19 2 1 1 2 3 4 5 6 7 8 9 10 x 1 30

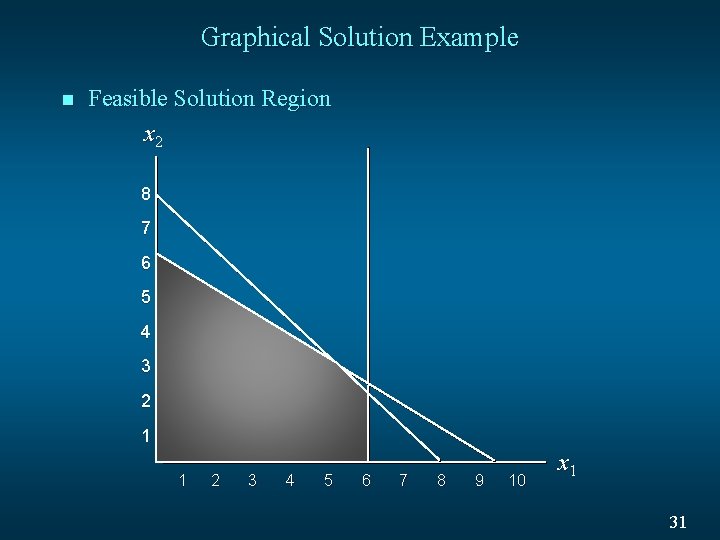
Graphical Solution Example n Feasible Solution Region x 2 8 7 6 5 4 3 Feasible Region 2 1 1 2 3 4 5 6 7 8 9 10 x 1 31

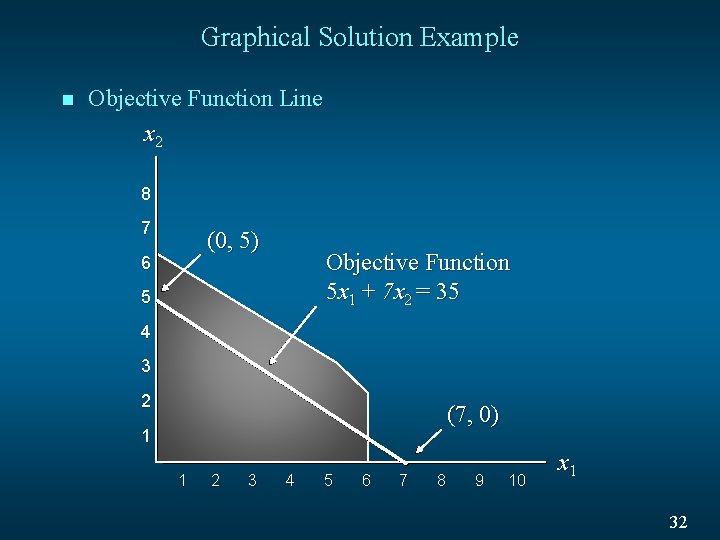
Graphical Solution Example n Objective Function Line x 2 8 7 (0, 5) 6 Objective Function 5 x 1 + 7 x 2 = 35 5 4 3 2 (7, 0) 1 1 2 3 4 5 6 7 8 9 10 x 1 32

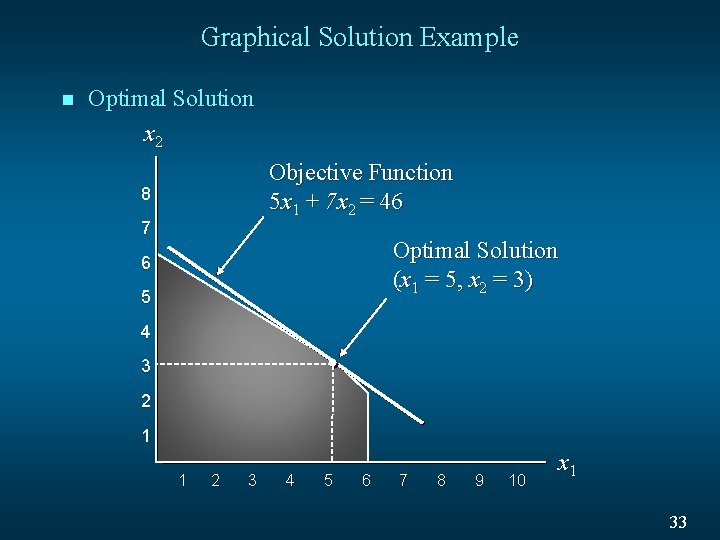
Graphical Solution Example n Optimal Solution x 2 Objective Function 5 x 1 + 7 x 2 = 46 8 7 Optimal Solution (x 1 = 5, x 2 = 3) 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 x 1 33

Graphical Linear Programming 1. Set up objective function and constraints in mathematical format 2. Plot the constraints 3. Identify the feasible solution space 4. Plot the objective function 5. Determine the optimum solution 34

Possible Outcomes of a LP · A LP is either Infeasible – there exists no solution which satisfies all constraints and optimizes the objective function · or, Unbounded – increase/decrease objective function as much as you like without violating any constraint · or, Has an Optimal Solution · · · Optimal values of decision variables Optimal objective function value 35

Infeasible LP – An Example minimize 4 x 11+7 x 12+7 x 13+x 14+12 x 21+3 x 22+8 x 23+8 x 24+8 x 31+10 x 32+16 x 33+5 x 34 Subject to · x 11+x 12+x 13+x 14=100 · x 21+x 22+x 23+x 24=200 · x 31+x 32+x 33+x 34=150 · · x 11+x 21+x 31=80 x 12+x 22+x 32=90 x 13+x 23+x 33=120 x 14+x 24+x 34=170 · xij>=0, i=1, 2, 3; j=1, 2, 3, 4 · · · Total demand exceeds total supply 36

Unbounded LP – An Example maximize 2 x 1 + x 2 subject to -x 1 + x 2 1 x 1 - 2 x 2 2 x 1 , x 2 0 x 2 can be increased indefinitely without violating any constraint => Objective function value can be increased indefinitely 37

Multiple Optima – An Example maximize x 1 + 0. 5 x 2 subject to 2 x 1 + x 2 4 x 1 + 2 x 2 3 x 1 , x 2 0 • x 1= 2, x 2=0, objective function = 2 • x 1= 5/3, x 2=2/3, objective function = 2 38