Lecture 3 Introduction to Waves and the wave

Lecture 3 - Introduction to Waves and the wave equation D Aims: ë Review of wave motion: >“Snapshots” and “waveforms”; >Wave equation. ë Harmonic waves: >Phase velocity. ë Representation of waves. >Plane waves: >1 -, 2 -, and 3 -D waves. >Spherical waves. 1 Waves 3

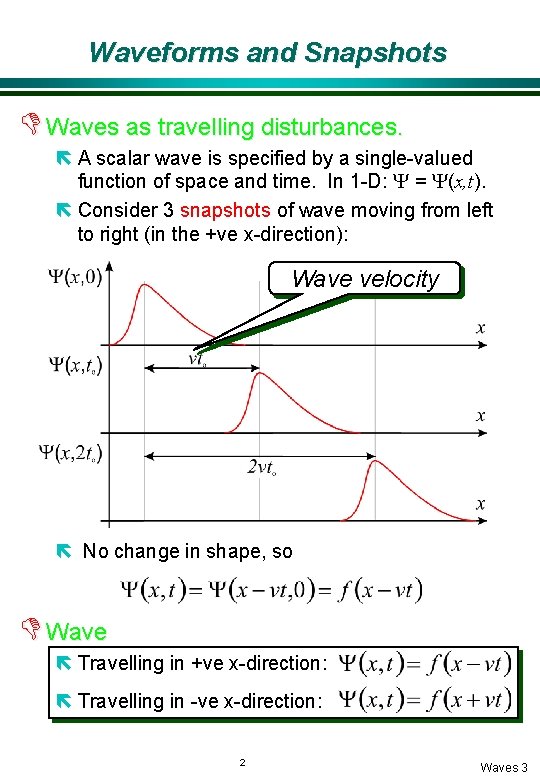
Waveforms and Snapshots D Waves as travelling disturbances. ë A scalar wave is specified by a single-valued function of space and time. In 1 -D: Y = Y(x, t). ë Consider 3 snapshots of wave moving from left to right (in the +ve x-direction): Wave velocity ë No change in shape, so D Wave ë Travelling in +ve x-direction: ë Travelling in -ve x-direction: 2 Waves 3

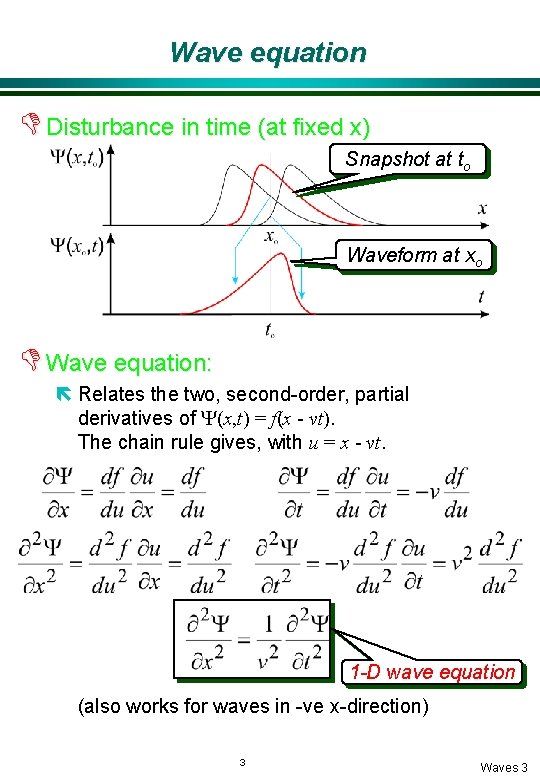
Wave equation D Disturbance in time (at fixed x) Snapshot at to Waveform at xo D Wave equation: ë Relates the two, second-order, partial derivatives of Y(x, t) = f(x - vt). The chain rule gives, with u = x - vt. 1 -D wave equation (also works for waves in -ve x-direction) 3 Waves 3

Wave equation: superposition D Important features: ë Generality: no specification of the type of wave. ë Linearity: all terms in Y are raised to first power only. Superposition is, thus, an implicit property. D Superposition: consider Y = Y 1 + Y 2. ë If Y 1 and Y 2 are solutions so is Y. ë Any linear combination of solutions is also a solution. >Basis of justification for Fourier analysis to describe wave properties. i. e. superposition of harmonic waves with different frequencies. 4 Waves 3

Harmonic waves D Wave varies sinusoidally (with both x and t). ë Require f(x-vt) {or equivalently f(t-x/v)} for a wave in the +ve x-direction. ë For harmonic dependence we need f(u) ~ eiwu. ë k is the wave-number, given by k = 2 p/l. ë v = w/k - Phase velocity of the wave ë In -ve x-direction D Nomenclature and convention: ë The following are equally valid for a wave in the +ve x-direction: ë There is no “agreed convention”. In general we use the i(wt-kx) form. The i(kx-wt) form is common in optics and quantum theory. ë The following are equivalent: Use this form 5 Waves 3

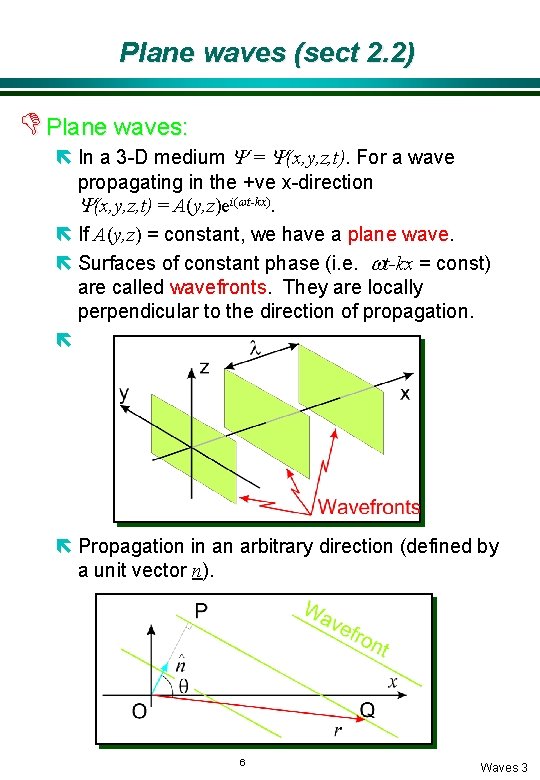
Plane waves (sect 2. 2) D Plane waves: ë In a 3 -D medium Y = Y(x, y, z, t). For a wave propagating in the +ve x-direction Y(x, y, z, t) = A(y, z)ei(wt-kx). ë If A(y, z) = constant, we have a plane wave. ë Surfaces of constant phase (i. e. wt-kx = const) are called wavefronts. They are locally perpendicular to the direction of propagation. ë ë Propagation in an arbitrary direction (defined by a unit vector n). 6 Waves 3

3 -D plane-wave D Wavevector ë Phase at Q = phase at P Wavevector ë Vector is the wavevector. It is in the direction of propagation and has magnitude 2 p/l. D General 3 -D plane-wave Plane wave ë it is the solution of the 3 -D wave equation Wave equation 7 Waves 3

Spherical waves D Waves expanding symmetrically from a point source. ë Conservation of energy demands the amplitude decreases with distance from the source. ë Since energy is proportional to|Y|2, energy flowing across a sphere of radius r is proportional to 4 pr 2 |Y|2. Thus Yµ 1/r. ë Spherical wave: Spherical wave ë At large r, it approximates a plane wave. D Summary ë General wave: ë 1 -D wave equation ë 3 -D plane wave ë 3 -D wave equation ë Spherical wave 8 Waves 3