Lecture 3 Hash Tables Cp Sc 212 Algorithms

Lecture 3. Hash Tables Cp. Sc 212: Algorithms and Data Structures Brian C. Dean School of Computing Clemson University Fall, 2012

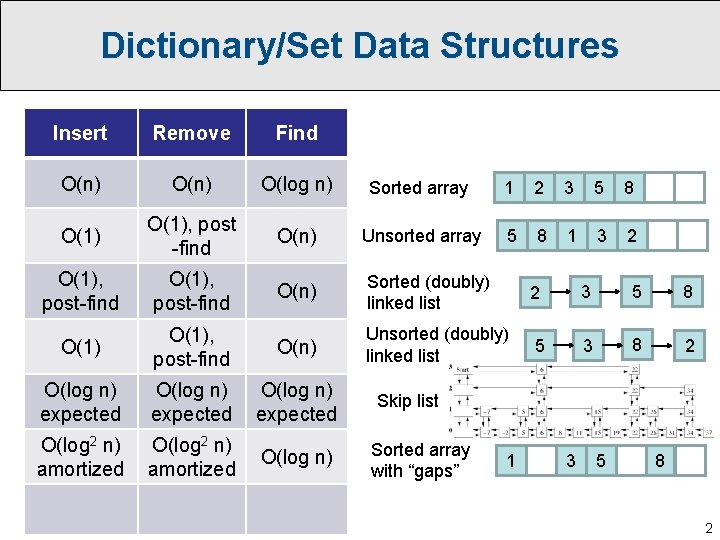
Dictionary/Set Data Structures Insert Remove Find O(n) O(log n) Sorted array 1 2 3 5 8 O(1), post -find O(n) Unsorted array 5 8 1 3 2 O(1), post-find O(n) Sorted (doubly) linked list 2 3 5 8 O(1), post-find O(n) Unsorted (doubly) linked list 5 3 8 2 O(log n) expected O(log 2 n) amortized O(log n) Skip list Sorted array with “gaps” 1 3 5 8 2

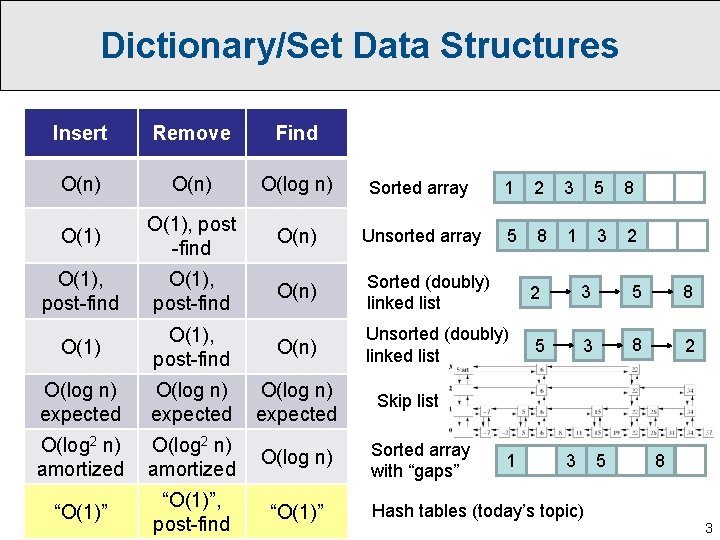
Dictionary/Set Data Structures Insert Remove Find O(n) O(log n) Sorted array 1 2 3 5 8 O(1), post -find O(n) Unsorted array 5 8 1 3 2 O(1), post-find O(n) Sorted (doubly) linked list 2 3 5 8 O(1), post-find O(n) Unsorted (doubly) linked list 5 3 8 2 O(log n) expected O(log 2 n) amortized O(log n) “O(1)”, post-find “O(1)” Skip list Sorted array with “gaps” 1 3 Hash tables (today’s topic) 5 8 3

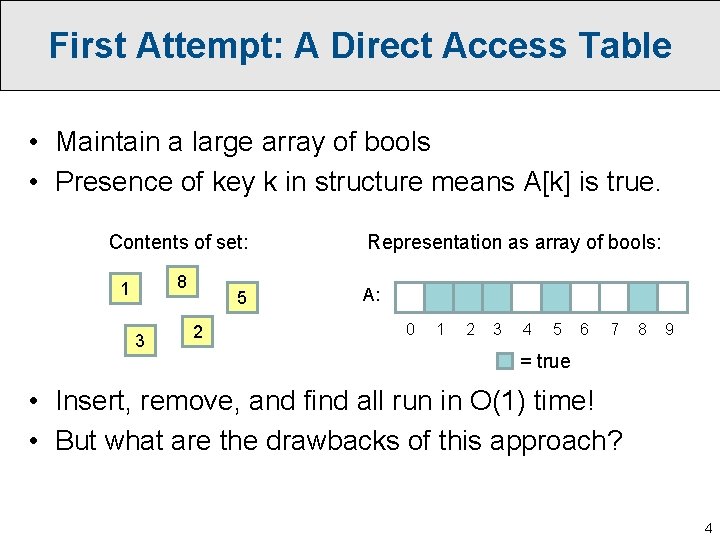
First Attempt: A Direct Access Table • Maintain a large array of bools • Presence of key k in structure means A[k] is true. Contents of set: 8 1 3 5 2 Representation as array of bools: A: 0 1 2 3 4 5 6 7 8 9 = true • Insert, remove, and find all run in O(1) time! • But what are the drawbacks of this approach? 4

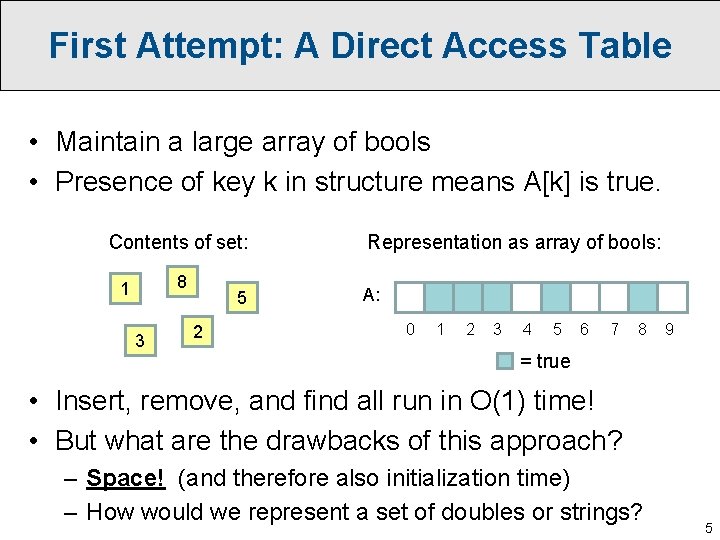
First Attempt: A Direct Access Table • Maintain a large array of bools • Presence of key k in structure means A[k] is true. Contents of set: 8 1 3 5 2 Representation as array of bools: A: 0 1 2 3 4 5 6 7 8 9 = true • Insert, remove, and find all run in O(1) time! • But what are the drawbacks of this approach? – Space! (and therefore also initialization time) – How would we represent a set of doubles or strings? 5

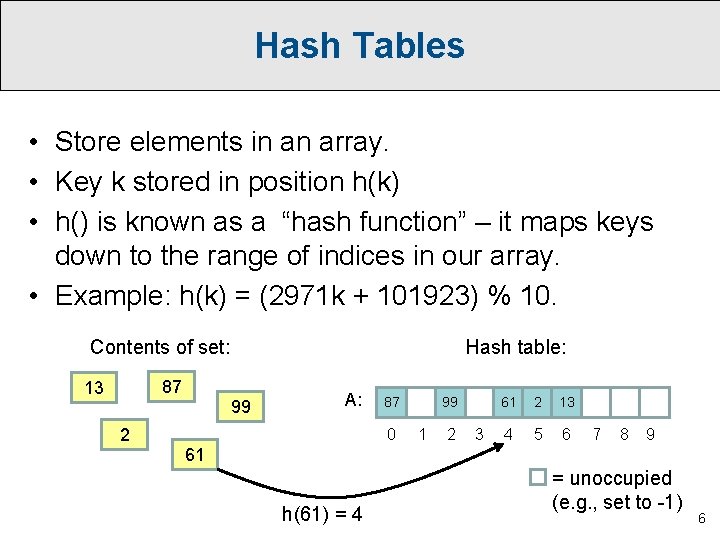
Hash Tables • Store elements in an array. • Key k stored in position h(k) • h() is known as a “hash function” – it maps keys down to the range of indices in our array. • Example: h(k) = (2971 k + 101923) % 10. Contents of set: 87 13 2 Hash table: 99 A: 87 0 99 1 2 3 61 2 13 4 5 6 7 8 9 61 h(61) = 4 = unoccupied (e. g. , set to -1) 6

Hash Tables: Positive Features • Can store doubles, strings, structs, or even more exotic types of data, as long as we can hash it. E. g. , h( ) = 8. • Space required for hash table is quite small; ideally we use only O(N) space for storing N elements. A: 0 1 2 3 4 5 6 7 8 9 7

Brief Aside: Integers and Overflow • A single byte (an 8 -bit integer) can hold a value in the range 0 … 255. • In C/C++, this is an “unsigned char”. • By contrast, “char x” declares a signed variable x; since one bit is used to hold the +/- sign, the range of values it can hold is now -128 … +127. • Watch out for overflow! What is the output of: char x = 127; x++; cout << x << “n”; • Same issue with ints (signed -2, 147, 483, 648 … +2, 147, 483, 647, unsigned 0 … 4, 294, 967, 295). 8

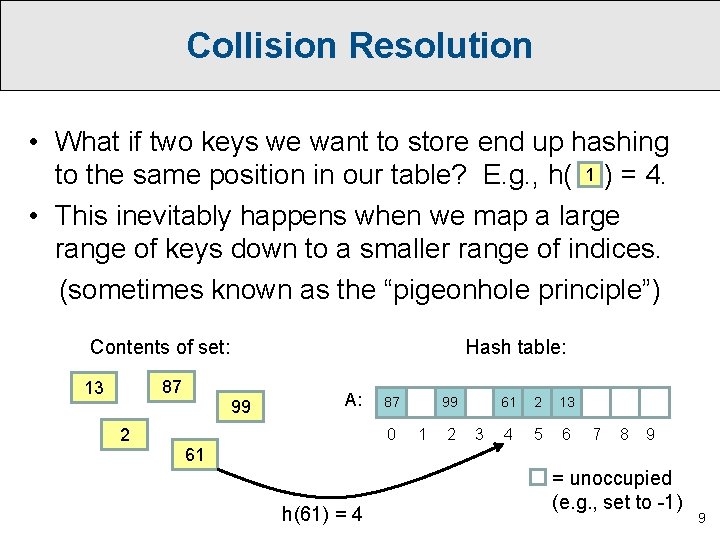
Collision Resolution • What if two keys we want to store end up hashing to the same position in our table? E. g. , h( 1 ) = 4. • This inevitably happens when we map a large range of keys down to a smaller range of indices. (sometimes known as the “pigeonhole principle”) Contents of set: 87 13 2 Hash table: 99 A: 87 0 99 1 2 3 61 2 13 4 5 6 7 8 9 61 h(61) = 4 = unoccupied (e. g. , set to -1) 9

Collision Resolution With Probing • If collision detected on insert, keep scanning forward until we reach an empty slot. • Find(k): start at position h(k) and scan forward until we either reach key k or an empty slot. • Performance will be good as long as table size is slightly larger than N, and our hash function spreads elements around “haphazardly” to avoid big clumps. A: 87 99 61 2 13 1 • What about remove(k)? 0 1 2 3 4 5 6 7 8 9 1 h(1) = 4 = unoccupied (e. g. , set to -1) 10

Collision Resolution With Probing • If collision detected on insert, keep scanning forward until we reach an empty slot. • Find(k): start at position h(k) and scan forward until we either reach key k or an empty slot. • Performance will be good – “O(1)” – as long as table size is slightly larger than N, and our hash function spreads elements around “haphazardly” to avoid big clumps. A: 87 99 61 13 1 • What about remove(k)? 0 1 2 3 4 5 6 7 8 9 – Mark k’s former position with a “tombstone”… remove(2) 11

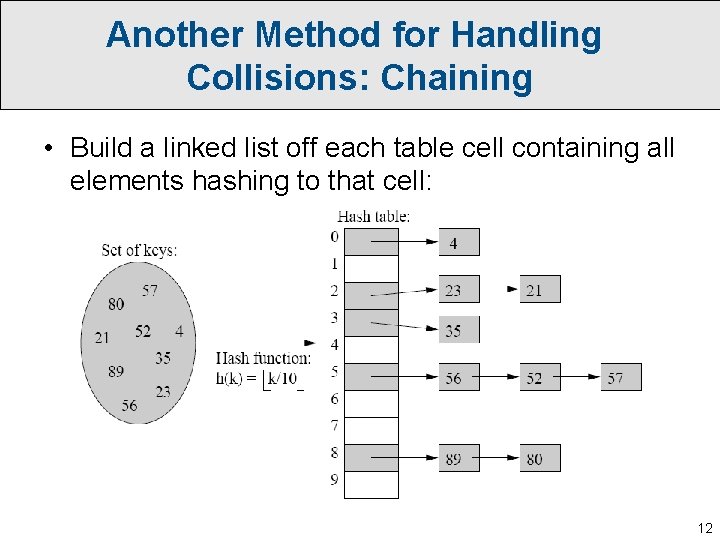
Another Method for Handling Collisions: Chaining • Build a linked list off each table cell containing all elements hashing to that cell: 12

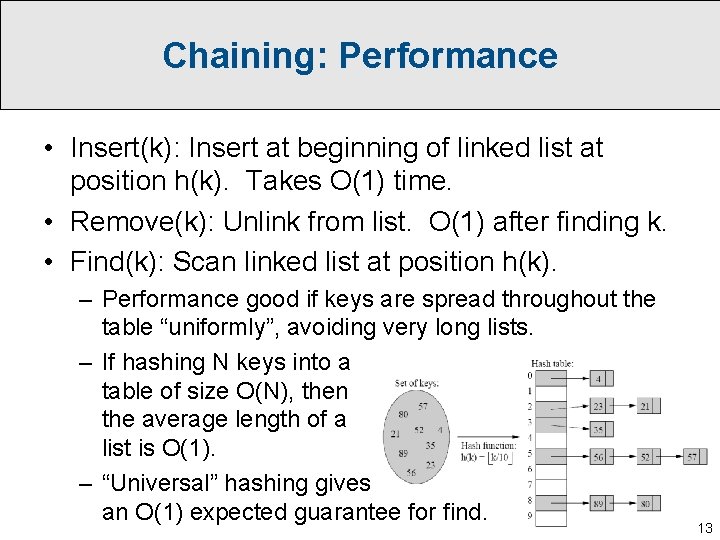
Chaining: Performance • Insert(k): Insert at beginning of linked list at position h(k). Takes O(1) time. • Remove(k): Unlink from list. O(1) after finding k. • Find(k): Scan linked list at position h(k). – Performance good if keys are spread throughout the table “uniformly”, avoiding very long lists. – If hashing N keys into a table of size O(N), then the average length of a list is O(1). – “Universal” hashing gives an O(1) expected guarantee for find. 13

Why “Hashing”…? Hash (n) A dish of cooked meat cut into small pieces and recooked, usually with potatoes. 14

Why “Hashing”…? Hash (n) A dish of cooked meat cut into small pieces and recooked, usually with potatoes. Hash (v) To jumble or mix up. 15

Choosing a Good Hash Function In Practice • We want h() to behave somewhat “randomly”. • Good Examples: m = table size – – = max possible h(k) = k mod m. C key value h(k) = mk / C. a and b should be chosen in a somewhat h(k) = (ak) mod m. “arbitrary” fashion (primes often used). h(k) = (ak + b) mod m. • Be sure to fully utilize “all the bits” in a key. For example, h(k) = k mod 256 is a somewhat poor hash function if k is a 32 -bit IP address. • Be sure to use the entire hash table; e. g. , make sure h(k) isn’t always even. 16

To Consider Moving Forward… • How do we pick the initial size of our table? • What if we need to insert more items than we anticipated? • How do we hash a large object like a string or an entire file? • Another nice collision resolution technique: cuckoo hashing! • Applications of hashing beyond data structures: security, networking, text searching, data mining, etc.