Lecture 3 Genome Rearrangements and Duplications Breakpoint graph

Lecture 3: Genome Rearrangements and Duplications

Breakpoint graph 1 -dimensional construction n Transform = < 2, -4, -3, 5, -8, -7, -6, 1 > into = < 1, 2, 3, 4, 5, 6, 7, 8 > by reversals. n Vertices: i ® ia ib -i ® ib ia and 0 b, 9 a Edges: match the ends of consecutive blocks in , n Superimpose matchings n

Breakpoint graph Breakpoints Each reversal goes between 2 breakpoints, so d ³ # breakpoints / 2 = 6/2 = 3. n Theorem (Hannenhalli-Pevzner 1995): d=n+1–c+h+f where c = # cycles; h, f are rather complicated, but can be computed from graph in polynomial time. n Here, d = 8 + 1 – 5 + 0 = 4 n

Breakpoint graph Þ rearrangement scenario

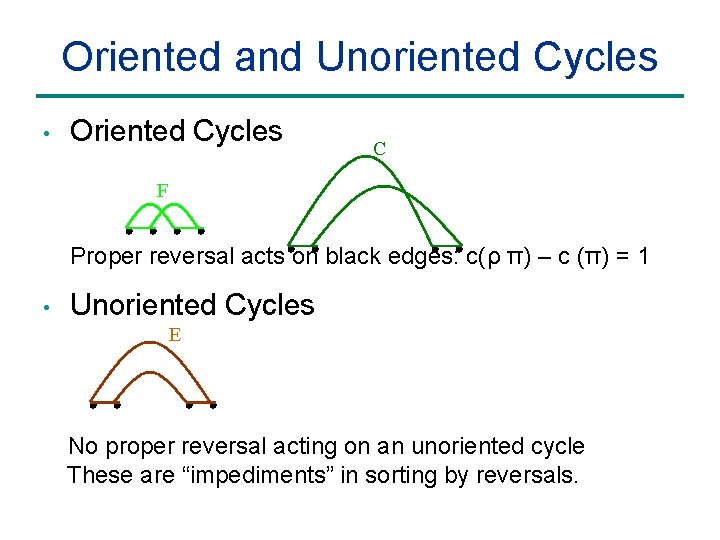
Oriented and Unoriented Cycles • Oriented Cycles C F Proper reversal acts on black edges: c(ρ π) – c (π) = 1 • Unoriented Cycles E No proper reversal acting on an unoriented cycle These are “impediments” in sorting by reversals.

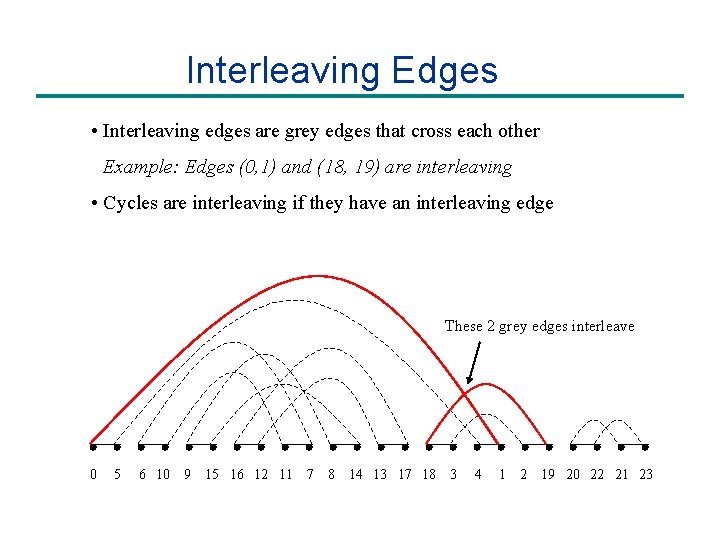
Interleaving Edges • Interleaving edges are grey edges that cross each other Example: Edges (0, 1) and (18, 19) are interleaving • Cycles are interleaving if they have an interleaving edge These 2 grey edges interleave 0 5 6 10 9 15 16 12 11 7 8 14 13 17 18 3 4 1 2 19 20 22 21 23

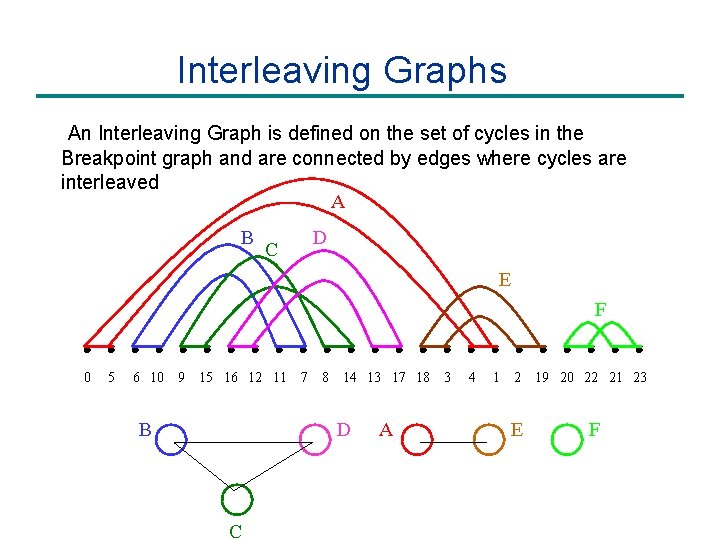
Interleaving Graphs An Interleaving Graph is defined on the set of cycles in the Breakpoint graph and are connected by edges where cycles are interleaved A B D C E F 0 5 6 10 9 15 16 12 11 B 7 8 14 13 17 18 D C A 3 4 1 2 E 19 20 22 21 23 F

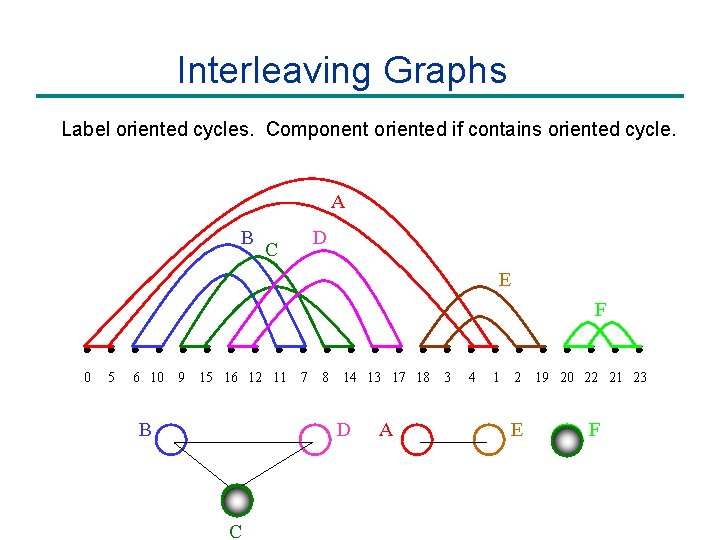
Interleaving Graphs Label oriented cycles. Component oriented if contains oriented cycle. A B D C E F 0 5 6 10 9 15 16 12 11 B 7 8 14 13 17 18 D C A 3 4 1 2 E 19 20 22 21 23 F

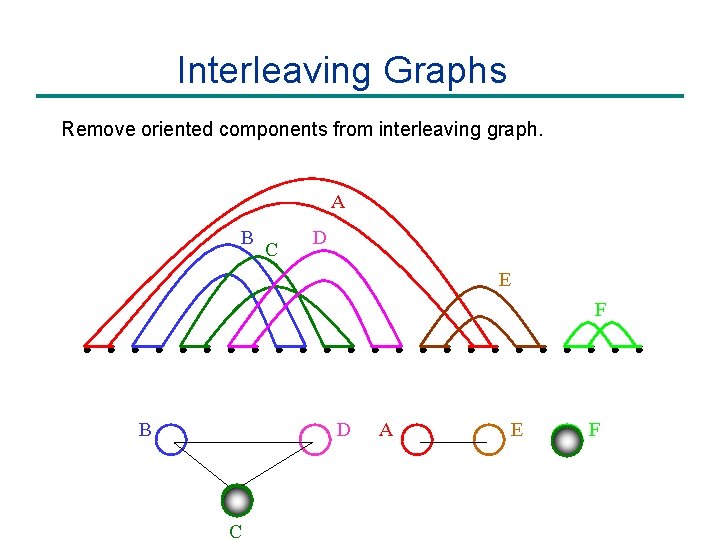
Interleaving Graphs Remove oriented components from interleaving graph. A B C D E F B D C A E F

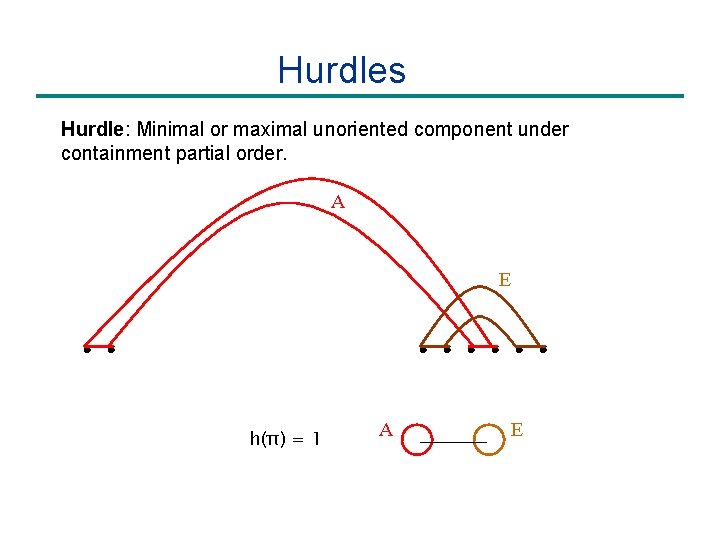
Hurdles Hurdle: Minimal or maximal unoriented component under containment partial order. A E h(π) = 1 A E

Reversal Distance with Hurdles • Hurdles are obstacles in the genome rearrangement problem • They cause a higher number of required reversals for a permutation to transform into the identity permutation 3 2 1 3 -1 -2 1 -3 -2 1 2 3 c(π) = 2, h(π) = 1 Every hurdle can be transformed into oriented cycles by reversal on arbitrary cycle in hurdle.

Reversal Distance with Hurdles • Hurdles are obstacles in the genome rearrangement problem • They cause a higher number of required reversals for a permutation to transform into the identity permutation • Let h(π) be the number of hurdles in permutation π • Taking into account of hurdles, the following formula gives a tighter bound on reversal distance: d(π) ≥ n+1 – c(π) + h(π) Every hurdle can be transformed into oriented cycles by reversal on arbitrary cycle in hurdle. ** Doing so, might cause problems with overlapping hurdles

Superhurdles • “Protect” non-hurdles • Deletion of superhurdles creates another hurdle

Superhurdles • “Protect” non-hurdles • Deletion of superhurdles creates another hurdle Superhurdle

Superhurdles • “Protect” non-hurdles • Deletion of superhurdles creates another hurdle Hurdle

Fortresses • A permutation π with an odd number of hurdles, all of which are superhurdles Theorem (Hannenhalli-Pevzner 1995): d(π) = n + 1 – c(π) + h(π) + f where c = # cycles; h = # hurdles f = 1 if π is fortress.

GRIMM-Synteny on X chromosome 2 -dimensional breakpoint graph

GRIMM-Synteny on X chromosome 2 -dimensional breakpoint graph

Coming Next 1. Other rearrangement operations Duplications 2. Rearrangements and Phylogeny Multiple Genomic Distance Problem: Given permutations 1, …, k find a permutation such that k=1, k d( 1, ) is minimal.

Other Types of Rearrangements So far: • • Discussed reversals. Also: translocations, fissions, fusions (modeled as reversals in concatenate of chromosomes (5 9 4 10) (– 6 – 1 11 7 – 2) (5 9 11 7 – 2) (– 6 – 1 4 10)

Other Types of Rearrangements • Transpositions 123456 • 125346 Duplication Transposition 123456 12345346 Duplications are very frequent in cancer genomes.

Duplications What problem to solve? Given G {1, . . , n}N (“permutation with duplicates”) Find reversals 1, 2, …, t, duplications 1, …, s, and permutation such that ( 1, …, t, 1, …, s) i = G and s + t is minimal 123456 ? ? ? 1 2 3 4 5 3 4 -2 -3 6 HARD!!! (NP-hard? )

Duplications (2) What problem to solve? Given: G {1, . . , n}N (“permutation with duplicates”) , H = G for some permutation Find: Reversals 1, 2, …, t such that 1 … t G = H and t is minimal Signed reversal distance with duplicates NP-hard (Chen, et al. 2005) If 1 -1 mapping of repeated elements (orthologs) in G to H then problem reduces to reversal distance.

Duplications (3) What problem to solve? Given: P {1, . . , n}N (permutation with duplicates) Find: Permutation and reversals 1, 2, …, s, duplications 1, … t such that 1, …, s 1, …, t = P and t minimal. Solution when at most two duplicates per gene El-Mabrouk and Sankoff (2002)

Whole Genome Duplication • • Genome is doubled – extra copy of each element. Subsequently undergoes reversals. Genome Halving Problem. Given a duplicated genome P, recover the ancestral pre-duplicated genome R minimizing the reversal distance from the perfect duplicated genome R © R to the duplicated genome P. (El-Mabrouk and Sankoff 1998 -2003)

Whole Genome Duplication • • Genome is doubled – extra copy of each element. Subsequently undergoes reversals. If copies of each element labeled uniquely, then problem reduces to reversal distance problem.

Reversal Distance and Duplications • • • Let d(G, H) = reversal distance b/w G and H Problem of computing d(P, R R) is unsolved min. R d(P, R R) solvable in polynomial time

Breakpoint Graph p 0 2 0 h 2 t g 0 -4 2 h 4 h 1 0 h 1 t -3 4 t 3 h 2 1 h 2 t 5 3 t 5 t 3 2 h 3 t -8 5 h 8 h 4 3 h 4 t -7 8 t 7 h 5 4 h 5 t -6 7 t 6 h 6 5 h 6 t 1 t 7 6 h 7 t 9 1 h 9 t 8 7 h 8 t 9 8 h 9 t G( p, g ) 0 2 0 b 2 a -4 2 b 4 b -3 4 a 3 b 5 3 a 5 a -8 5 b 8 b -7 8 a 7 b -6 7 a 6 b 1 6 a 1 a 9 1 b 9 a

Genome Halving: Exhaustive • • Doubled genome with 2 n genes Compute reversal distance on all 2 n labeling of genes.

Genome Halving • Weak Genome Halving Problem. For a given duplicated genome P, find a perfect duplicated genome R © R and a labeling of gene copies that maximizes the number of black-gray cycles c(G) in the breakpoint graph G(P, R © R) of the labeled genomes P and R R. (Alekseyev and Pevzner 2006) Theorem (Hannenhalli-Pevzner 1995): d(π) = n + 1 – c(π) + h(π) + f where c = # cycles; h = # hurdles f = 1 if π is fortress.

Contracted Breakpoint Graph Breakpoint graph construction • p 0 2 0 h 2 t g 0 -4 2 h 4 h 1 0 h 1 t -3 4 t 3 h 2 1 h 2 t 5 3 t 5 t 3 2 h 3 t -8 5 h 8 h 4 3 h 4 t -7 8 t 7 h 5 4 h 5 t -6 7 t 6 h 6 5 h 6 t 1 t 7 6 h 7 t 9 1 h 9 t 8 7 h 8 t 9 8 h 9 t G( p, g ) 0 2 0 h 2 t -4 2 h 4 h -3 4 t 3 h 5 3 t 5 h -8 5 t 8 h -7 8 t 7 h -6 7 t 6 h Implicit were obverse edges (xt, xh) is black-obverse alternating path is gray-observe alternating path 1 6 t 1 t 9 1 h 9 t

Contracted Breakpoint Graph • • With duplicates, pair of vertices with same label. Contract these identical vertices

Contracted Breakpoint Graph P = −a−b+g+d+f+g+e−a+c−f−c−b−d−e R = −a−b−d−g+f−c−e G’(P, R © R) Each gray edge is pair of parallel edges

Cycle Decompositions Genomes P and Q G(P, Q) breakpoint graph for some labeling Black-gray cycle decomposition ? ? ? G’(P, Q) contracted breakpoint graph Induced black-gray cycle decomposition Labeling Problem. Given a black-gray cycle decomposition of the contracted breakpoint graph G′(P, Q) of duplicated genomes P and Q, find labeling of P and Q that induces this cycle decomposition.

Cycle Decomposition P = −a−b+g+d+f+g+e−a+c−f−c−b−d−e R = −a−b−d−g+f−c−e G’(P, R © R) BG graph corresponding to G’ Maximal black-gray cycle decomposition

Cycle Decomposition P = −a−b+g+d+f+g+e−a+c−f−c−b−d−e R = −a−b−d−g+f−c−e P as black-observe cycle

Genome Halving Algorithm: Outline Input: Doubled genome P 1. 2. 3. 4. 5. Construct BO (black-obverse) graph for P by gluing identical edges Introduce gray edges “optimally” to create BOG (black-observe-gray) graph G’ with single grayobserve cycle (!!!) R = gray-observe cycle in G’ Find maximal black-gray cycle decomposition of G’ Q=R R