Lecture 3 First and Second Law of Thermodynamics

Lecture 3 First and Second Law of Thermodynamics

First Law of Thermodynamics FOR OPEN SYSTEMS Inserting expression for flow work and regrouping terms Recall enthalpy defn. : h=u+pv For rate processes dividing both sides by t and letting t 0 For large processes provided all inlet/outlet conditions are steady (not changing with time) integrate both sides

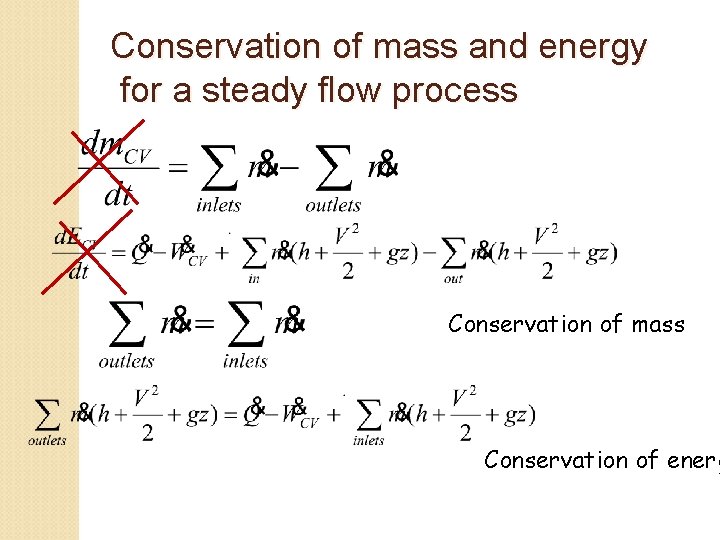
Conservation of mass and energy for a steady flow process Conservation of mass Conservation of energ

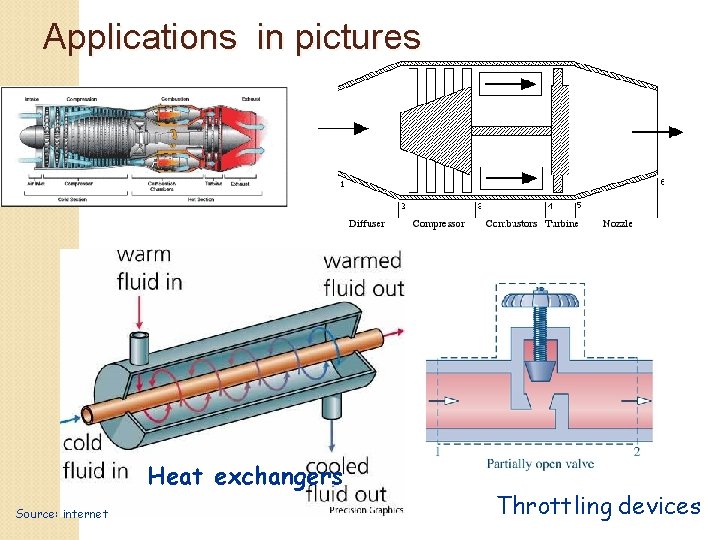
Applications Nozzles and diffusers (e. g. jet propulsion) Turbines (e. g. power plant, turbofan/turbojet aircraft engine), compressors and pumps (power plant) Heat exchangers (e. g. boilers and condensers in power plants, evaporator and condenser in refrigeration, food and chemical processing) Mixing chambers (power plants) Throttling devices (e. g. refrigeration, steam quality measurement in power plants)

Applications in pictures Heat exchangers Source: internet Throttling devices

nozzles/diffusers Single stream

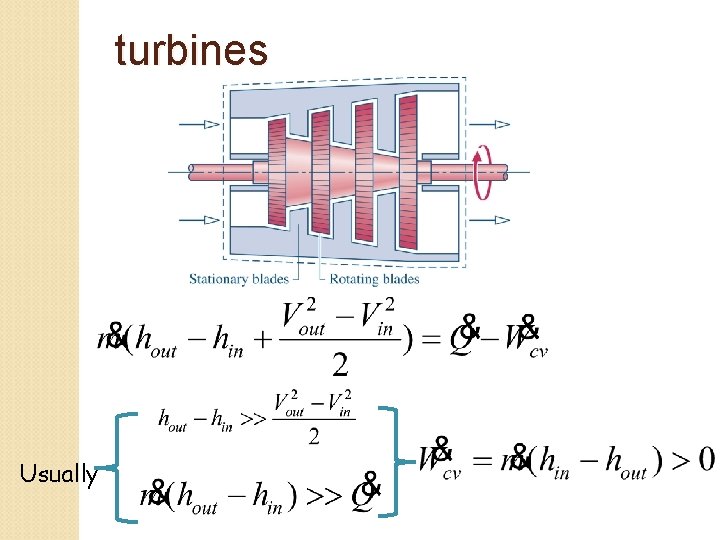
turbines Usually

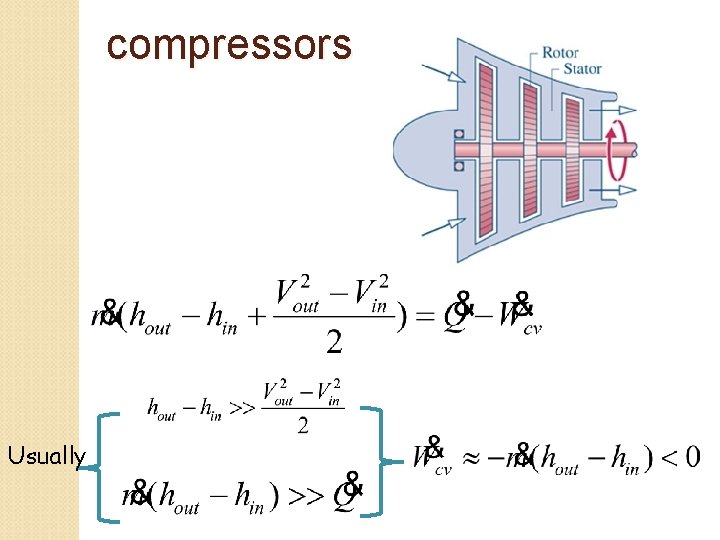
compressors Usually

heat exchangers hot (h) cold (c) Take CV enclosing the stream that is hot at inlet Take CV enclosing the stream that is cold at inlet

Mixing chambers or “direct contact heat exchangers” 3 2 1 Conservation of mass Conservation of energy

Principles of Thermodynamics

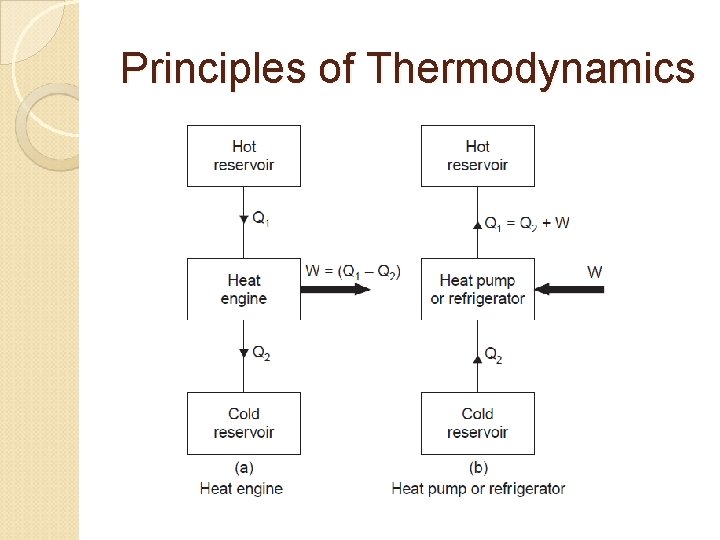
Thermal efficiency, where, W = Net work transfer from the engine, and Q 1 = Heat transfer to engine. Q 2 = Heat transfer from cold reservoir,

Clausius Statement “It is impossible for a self acting machine working in a cyclic process unaided by any external agency, to convey heat from a body at a lower temperature to a body at a higher temperature”. In other words, heat of, itself, cannot flow from a colder to a hotter body

Kelvin-Planck Statement “It is impossible to construct an engine, which while operating in a cycle produces no other effect except to extract heat from a single reservoir and do equivalent amount of work”.

Why does Q flow from hot to cold? q. Consider two systems, one with TA and one with TB q. Allow Q > 0 to flow from TA to TB q. Entropy changed by: DS = Q/TB - Q/TA q. If TA > TB, then DS > 0 q. System will achieve more randomness by exchanging heat until TB = TA

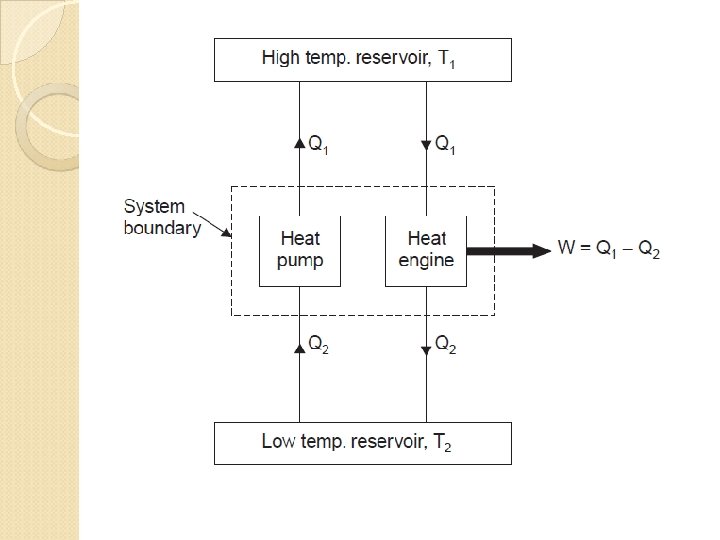
Efficiencies of Engines Consider a cycle described by: W, work done by engine Qhot, heat that flows into engine from source at Thot W Qcold, heat exhausted from engine at lower engine temperature, Tcold Efficiency is defined: Qcold Since ,

Carnot Engines Idealized engine Most efficient possible

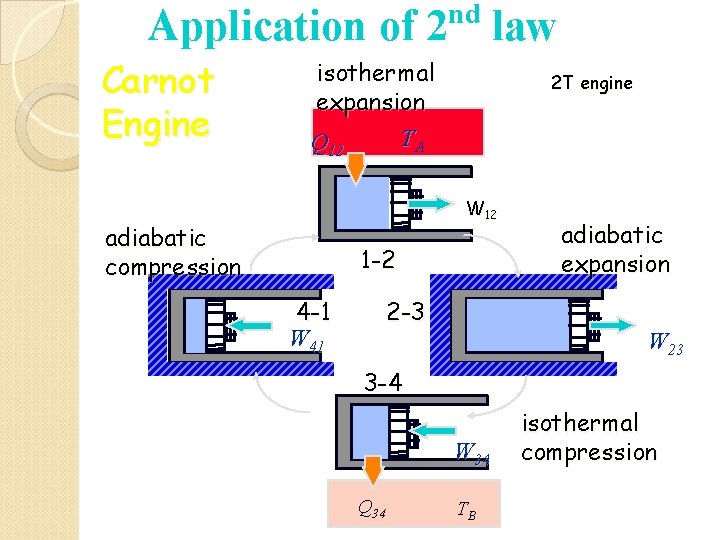
nd Application of 2 law Carnot Engine isothermal expansion TA Q 12 2 T engine W 12 adiabatic compression 1 -2 4 -1 W 41 2 -3 adiabatic expansion W 23 3 -4 W 34 Q 34 TB isothermal compression

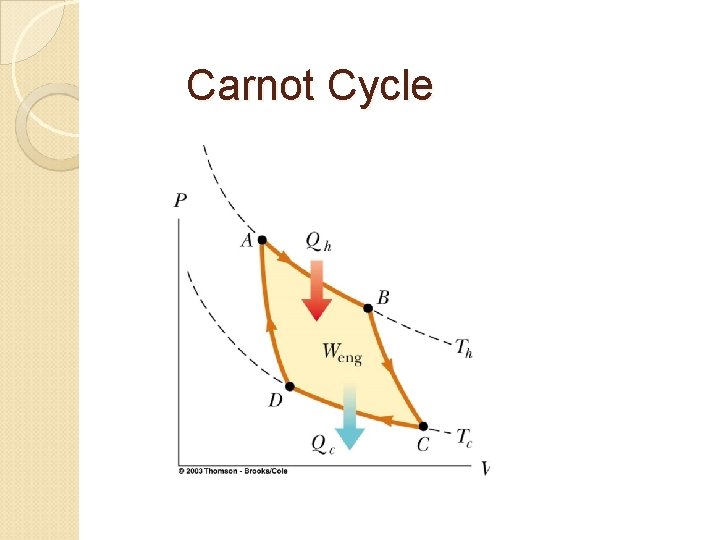
Carnot Cycle

Efficiency of a Carnot engine apply 1 st law for this cycle: then energy conversion efficiency is: for a reversible process:

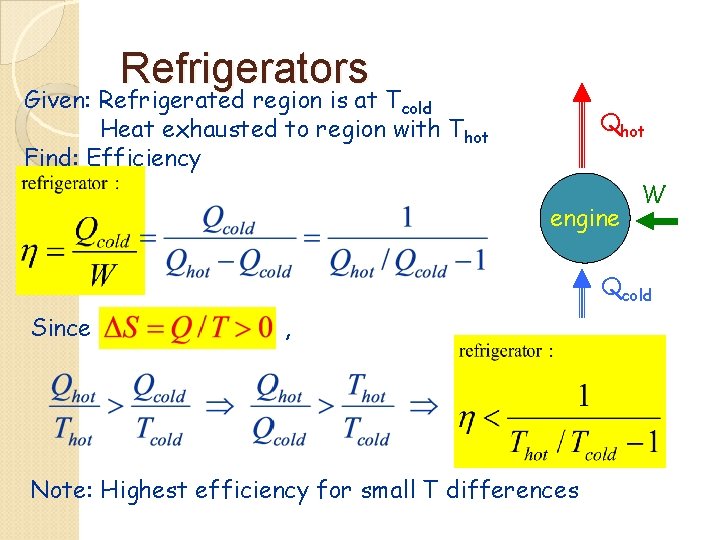
Refrigerators Given: Refrigerated region is at Tcold Heat exhausted to region with Thot Find: Efficiency Qhot engine W Qcold Since , Note: Highest efficiency for small T differences

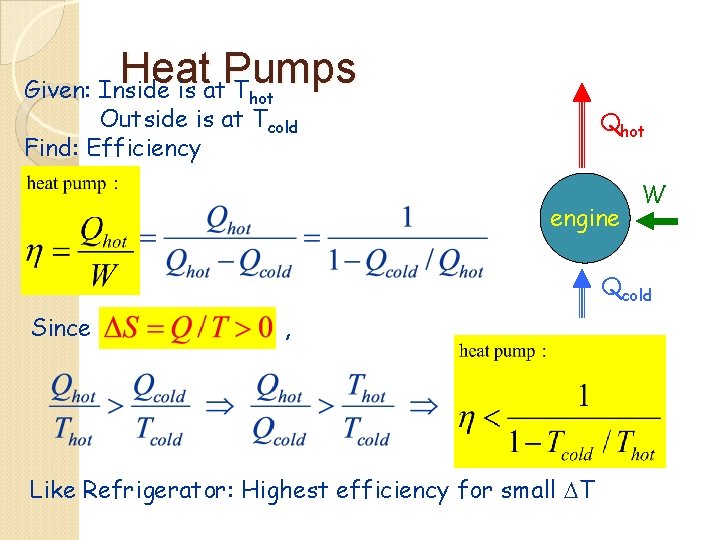
Heat Pumps Given: Inside is at T hot Outside is at Tcold Find: Efficiency Qhot engine W Qcold Since , Like Refrigerator: Highest efficiency for small DT

Entropy Total Entropy always rises! (2 nd Law of Thermodynamics) Adding heat raises entropy Defines temperature in Kelvin!