Lecture 3 Divide and Conquer Example 3 Integer

Lecture 3: Divide and Conquer

Example 3 Integer Multiplication • Input: two positive integers a, b • Output: a×b multiply(a, b) 1. RETURN a*b ? • What if a = 73489553479834257983745 and b = 197878967893267834267324789? • Naïve algorithm: O(n 2) time (learned in elementary school)

Divide and Conquer • a = 123, 456 b = 654, 321 • How to divide? • Write a = 123, 000 + 456, b = 654, 000 + 321. • Then a*b = 123*654*106 + (123*321+456*654)*103 + 456*321.

First attempt • Partition a = a 1*10 n/2+a 2, b = b 1*10 n/2+b 2 • Recursively compute A = a 1*b 1, B = a 2*b 1, C = a 1*b 2, D = a 2*b 2 • Output A*10 n+(B+C)*10 n/2+D Multiply(a, b) 1. (wlog assume n = length(a) = length(b), pad 0 for the shorter number) 2. IF Length(a) <= 1 THEN RETURN a*b 3. Partition a into a = a 1 * 10 n/2+a 2, b = b 1*10 n/2+b 2 4. A = Multiply(a 1, b 1) 5. B = Multiply(a 2, b 1) 6. C = Multiply(a 1, b 2) 7. D = Multiply(a 2, b 2) 8. RETURN A*10 n+(B+C)*10 n/2 + D Need an algorithm for adding long numbers. Standard algorithm suffices (O(n))

Improving the algorithm To make a divide and conquer algorithm faster 1. Make the merging step faster 2. Make the sub-problems smaller 3. Reduce the number of sub-problems • Observation: (a 1*b 2+a 2*b 1) = (a 1+a 2)*(b 1+b 2) – a 1*b 1 – a 2*b 2

Improved Algorithm • Partition a = a 1*10 n/2+a 2, b = b 1*10 n/2+b 2 • Recursively compute A = a 1*b 1, B = a 2*b 2, C = (a 1+a 2)*(b 1+b 2) • Output A*10 n+(C-A-B)*10 n/2+B Multiply(a, b) 1. (wlog assume n = length(a) = length(b), pad 0 for the shorter number) 2. IF Length(a) <= 1 THEN RETURN a*b 3. Partition a into a = a 1 * 10 n/2+a 2, b = b 1*10 n/2+b 2 4. A = Multiply(a 1, b 1) 5. B = Multiply(a 2, b 2) 6. C = Multiply(a 1+a 2, b 1+b 2) 7. RETURN A*10 n+(C-A-B)*10 n/2 + B

Master Theorem •

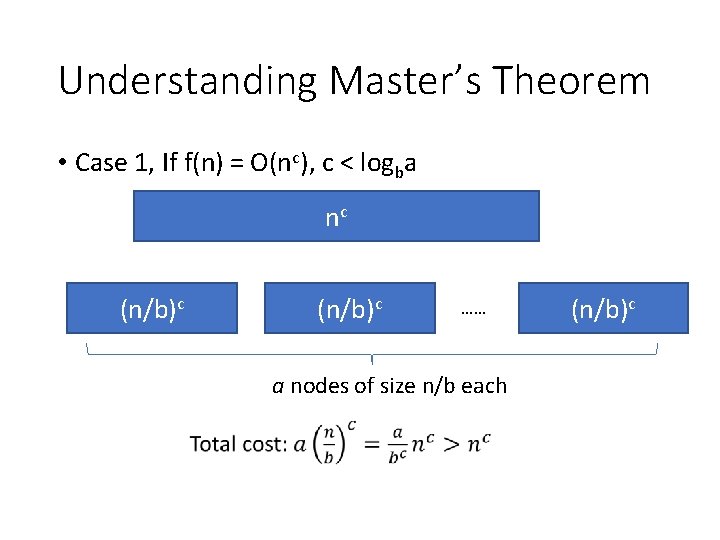
Understanding Master’s Theorem • Case 1, If f(n) = O(nc), c < logba nc (n/b)c …… a nodes of size n/b each (n/b)c

Understanding Master’s Theorem • Case 2, If f(n) = θ(nclogtn), c = logba nclogtn (n/b)clogt(n/b) …… (n/b)clogt(n/b)

Understanding Master’s Theorem • Case 3, If f(n) = O(nc), c > logba nc (n/b)c …… (n/b)c a nodes of size n/b each

Useful Facts about Log • log ab = log a + log b • logab = (log b) / (log a) • log ab = b log a • a^(logb c) = c^(logb a) • (easy to see if you take log b on both sides) • (logb a) (logb c) = (logb c) (logb a)