Lecture 3 Data Summary Measures and Graphical Display

Lecture 3 – Data Summary Measures and Graphical Display of Results Univariate Data – Analysis of one variable at a time

Why Think About/Explore Data? • Done to accomplish: – Checking for data entry errors – Describing demographic and study characteristics – Examining distributions of outcomes • Central tendency • Variability – Checking for outliers – Checking assumptions for subsequent analyses – Give a picture of your sample

• In order to understand choices of which statistics could be appropriate, it is paramount to ascertain what measurement level the outcome (s) and predictor (s) have. Dependent variable = outcome Independent variable = predictor

Types of Data Ø Nominal – Qualitative Data Measured in unordered categories (summarize with %’s): Ø Ordinal – Qualitative Data Measured in ordered categories (summarize with %’s): Ø Continuous – Quantitative Data Measured on a continuum summarize with Many Summary Measures

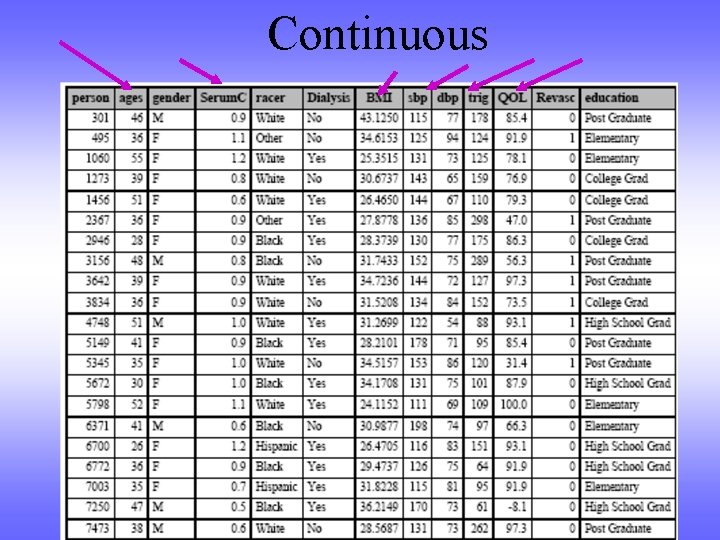
Types of Data Ø Nominal – Qualitative Data Measured in unordered categories Ø Race Ø Blood Type Ø Dead/Alive Ø Gender Ø On Dialysis/Not on Dialysis Ø Ordinal – Qualitative Data Measured in ordered ØLikert categories (unlikely, somewhat unlikely, neutral, Ø Continuous – Quantitative Data Measured a likely) likely, on very continuum Ø Systolic Blood Pressure Ø Serum Creatinine ØDiastolic Blood Pressure Ø Height/Weight/BMI ØOthers? ? ? Ø Cancer Stages Ø Socio-economic Status (low, med, hi)

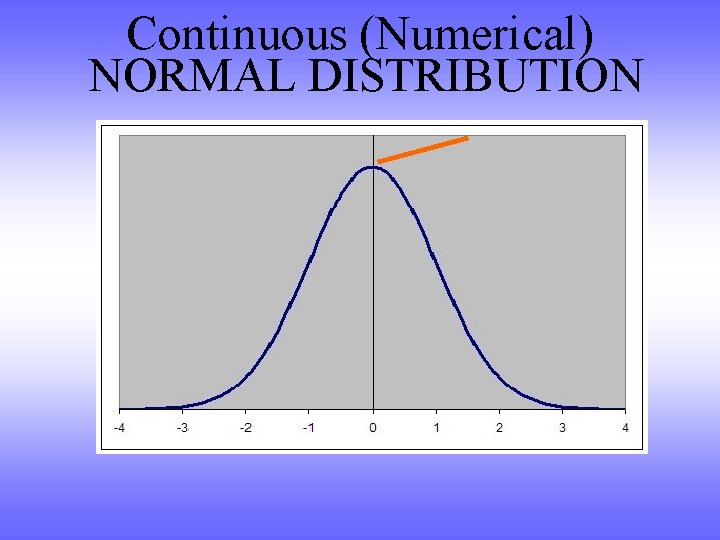
Continuous (Numerical) Ø Mean Measures of Location Arithmetic Average Sum of Values/Number of Values Nice mathematical/statistical properties Ø Median (a. k. a 50 th Percentile) Value where half the sample is above, half the sample is below Better measure for skewed data. Robust to Extreme values Ø Mode Most Frequently Occurring value in Sample

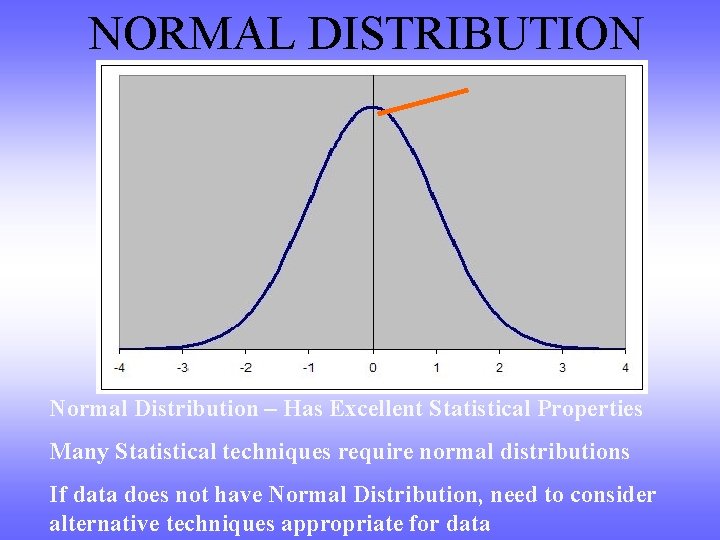
Continuous (Numerical) NORMAL DISTRIBUTION

Continuous (Numerical) Measures of Variability • Range = (maximum - minimum) • Interquartile range = (Q 3 – Q 1) always covers half the sample (75 th - 25 th percentile) • Variance = average of the squares of the deviations of the observations from their mean

Continuous (Numerical) NORMAL DISTRIBUTION http: //www. stattucino. com/berrie/dsl/index. html

Describing Data using Numerical Summaries ¨Descriptive statistics: Explore data in order to describe their main features Get an initial picture of data sample

Let’s Talk Data…

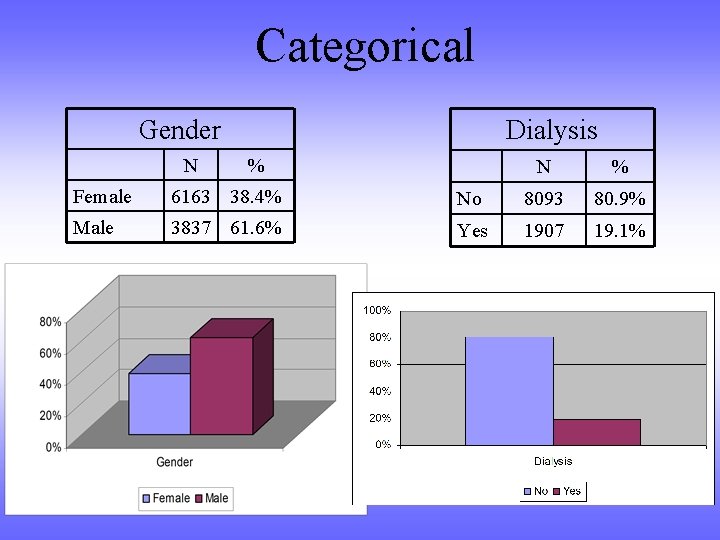
Categorical Dialysis Gender N % Female 6163 38. 4% No 8093 80. 9% Male 3837 61. 6% Yes 1907 19. 1%

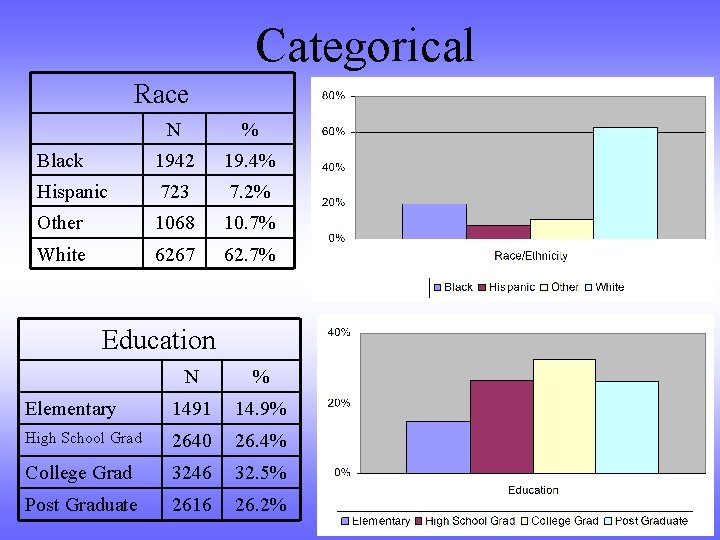
Categorical Race N % Black 1942 19. 4% Hispanic 723 7. 2% Other 1068 10. 7% White 6267 62. 7% Education N % Elementary 1491 14. 9% High School Grad 2640 26. 4% College Grad 3246 32. 5% Post Graduate 2616 26. 2%

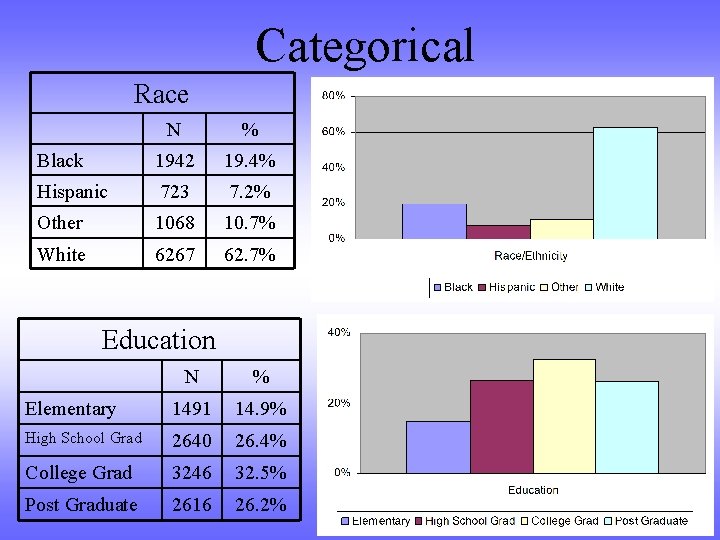
Categorical Race N % Black 1942 19. 4% Hispanic 723 7. 2% Other 1068 10. 7% White 6267 62. 7% Education N % Elementary 1491 14. 9% High School Grad 2640 26. 4% College Grad 3246 32. 5% Post Graduate 2616 26. 2%

Continuous

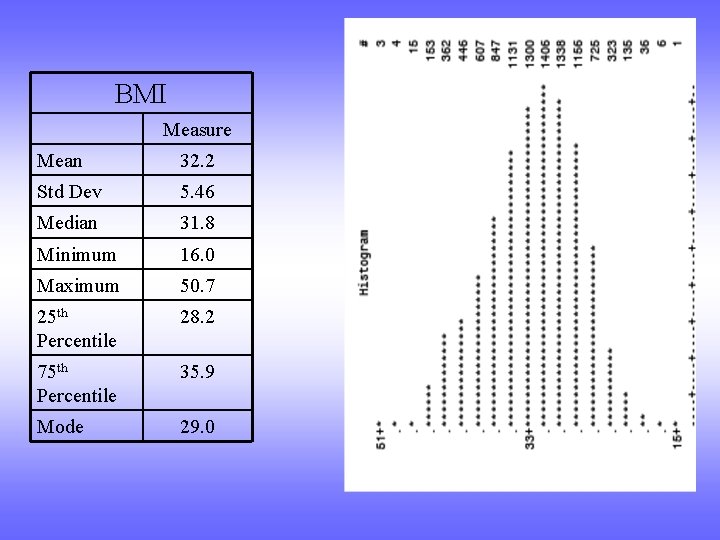
BMI Measure Mean 32. 2 Std Dev 5. 46 Median 31. 8 Minimum 16. 0 Maximum 50. 7 25 th Percentile 28. 2 75 th Percentile 35. 9 Mode 29. 0

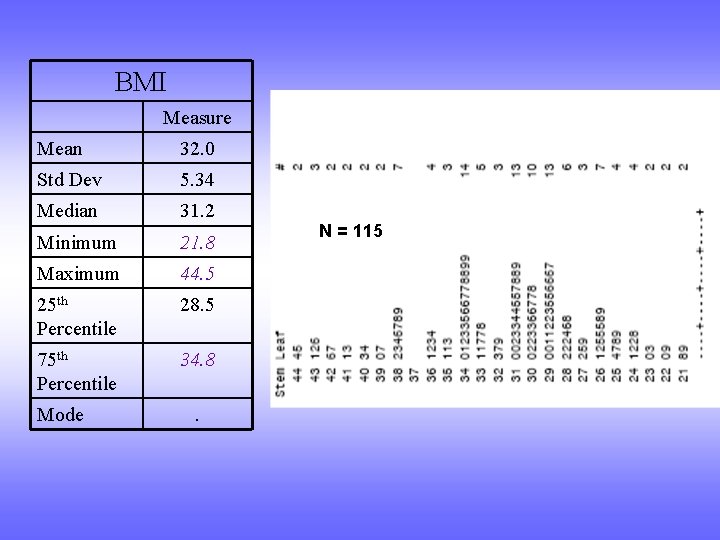
BMI Measure Mean 32. 0 Std Dev 5. 34 Median 31. 2 Minimum 21. 8 Maximum 44. 5 25 th Percentile 28. 5 75 th Percentile 34. 8 Mode . N = 115

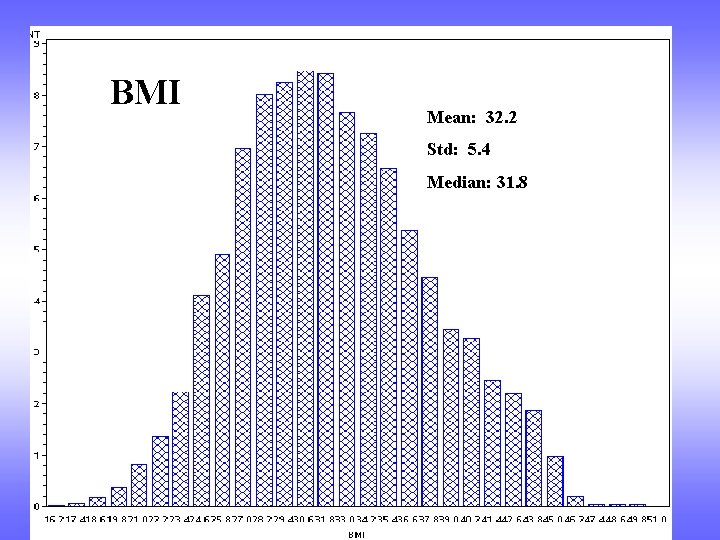
BMI Mean: 32. 2 Std: 5. 4 Median: 31. 8

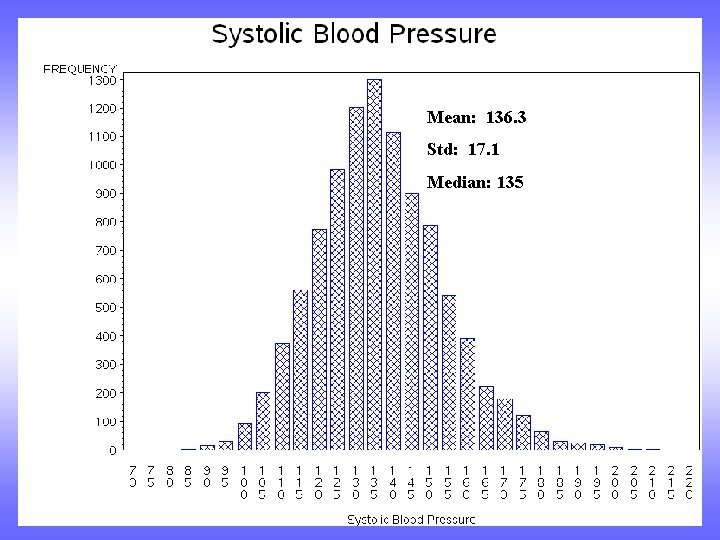
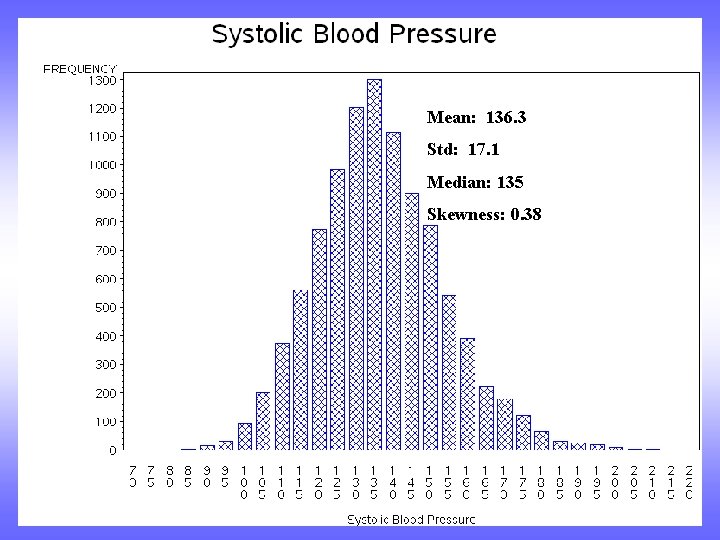
Mean: 136. 3 Std: 17. 1 Median: 135

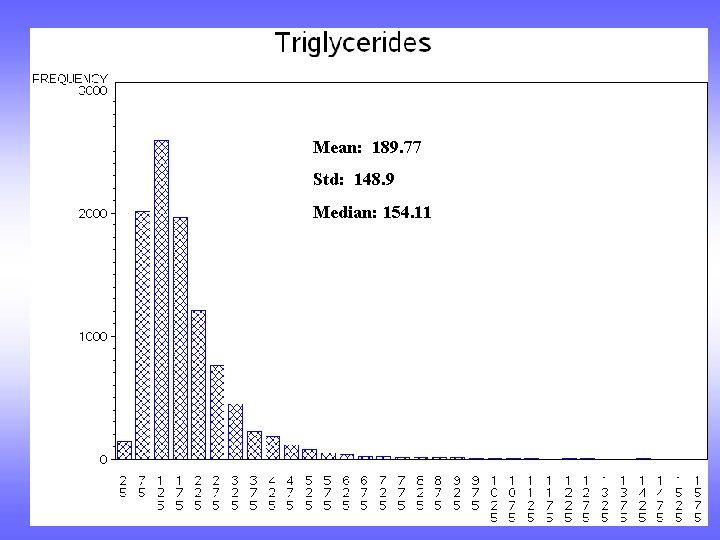
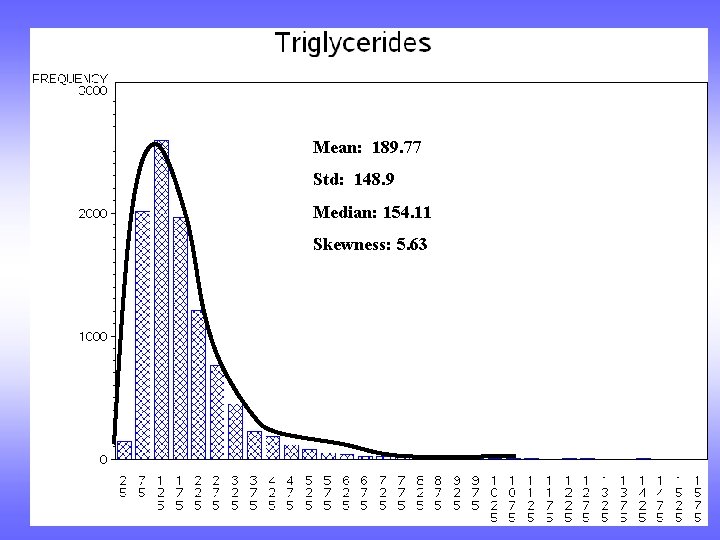
Mean: 189. 77 Std: 148. 9 Median: 154. 11

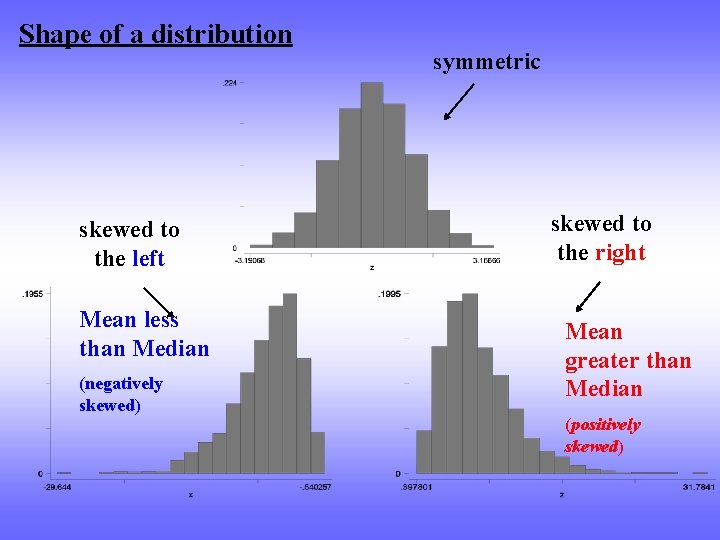
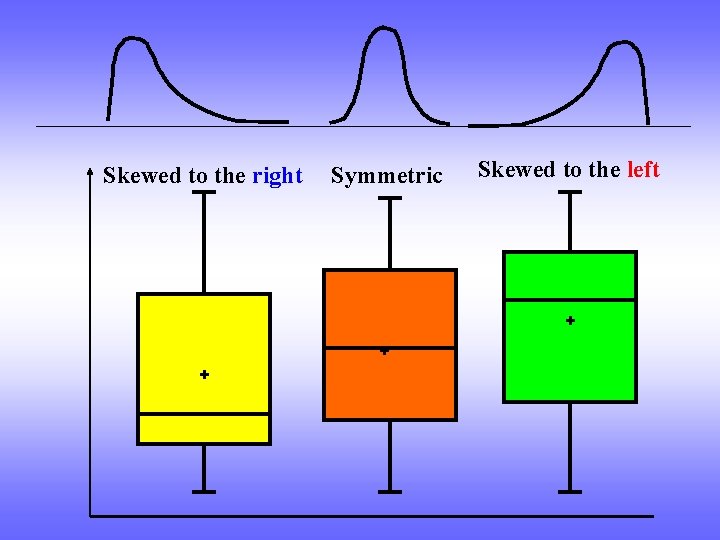
Shape of a distribution skewed to the left Mean less than Median (negatively skewed) symmetric skewed to the right Mean greater than Median (positively skewed)

Mean: 136. 3 Std: 17. 1 Median: 135 Skewness: 0. 38

Mean: 189. 77 Std: 148. 9 Median: 154. 11 Skewness: 5. 63

NORMAL DISTRIBUTION Normal Distribution – Has Excellent Statistical Properties Many Statistical techniques require normal distributions If data does not have Normal Distribution, need to consider alternative techniques appropriate for data

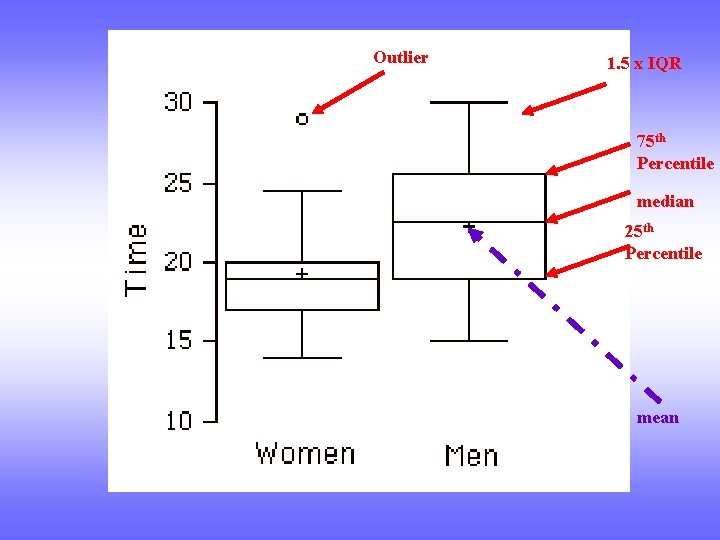
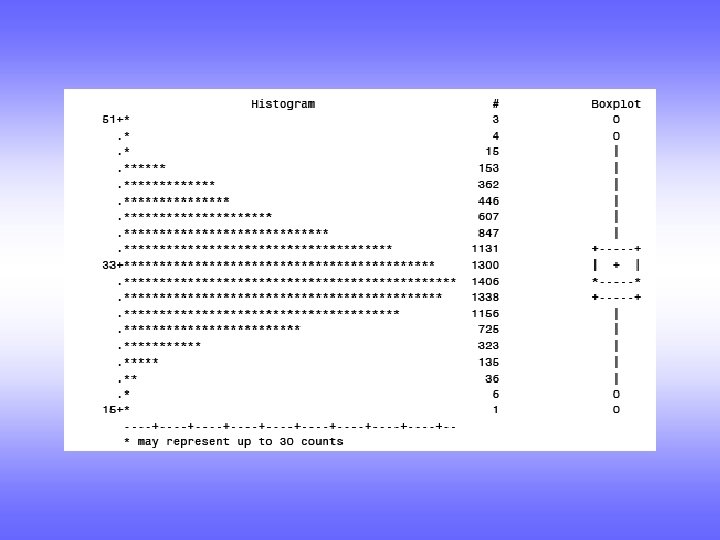
Box (and Whisker) Plots • A graph of the 5 number summary with suspected outliers plotted individually • 5 number summary: Min, Q 1, Median, Q 3, Max • A line somewhere inside the box marks the Median • IQR = Q 3 – Q 1 • Cases more than 1. 5*IQR are plotted individually (possible outliers) • Lines from the box extend to the smallest and largest values that are not more than 1. 5*IQR

Outlier 1. 5 x IQR 75 th Percentile median 25 th Percentile mean

Skewed to the right Symmetric Skewed to the left + + +

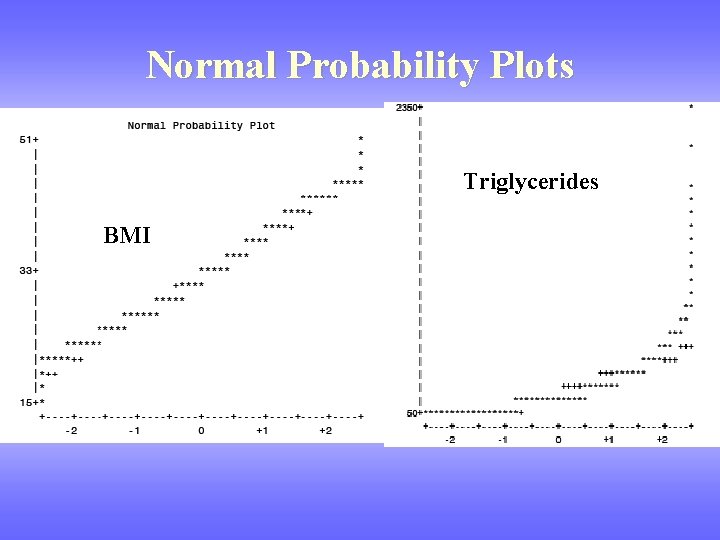
Normal Probability Plot • Plot that can help assess normality. • Idea: plot the observed levels of the variable against the expected levels corresponding to a Normal distribution. • If data lie in a reasonably straight diagonal line, then assumption of Normality is reasonable.

Normal Probability Plots Triglycerides BMI

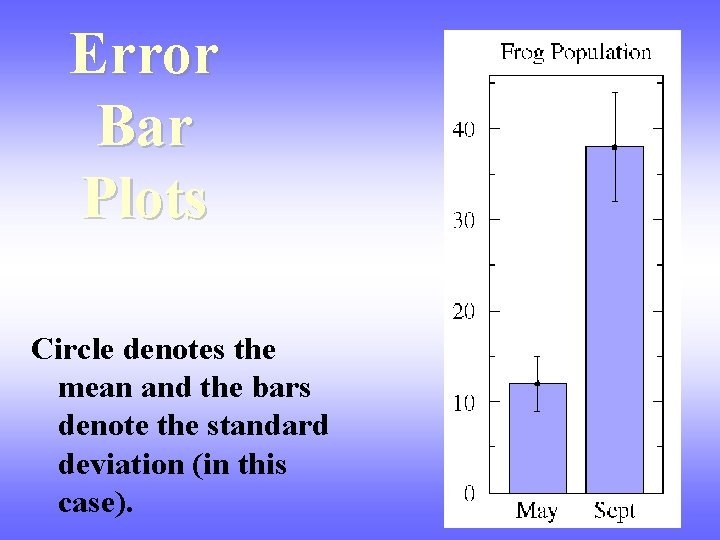
Error Bar Plots Circle denotes the mean and the bars denote the standard deviation (in this case).

Part II – Measures of Association (plus a little more)

Measures of Association • Continuous Variables – Correlation – Agreement (reliability) • Categorical Variables – Two-way layout (2× 2 tables) – “Risk” measures – Agreement – Others

Two Continuous Variables Correlation – General sense: the relationship between two variables (quantitative or qualitative) – Narrow (statistical) sense: measure of interdependence between two continuous random variables • The degree to which increases or decreases in Y occur with increases or decreases in X • Values range between -1 (perfect discordance) and 1 (perfect concordance) • A value of 0 indicates no association

Pearson Correlation Purpose - measures linear association between two continuous variables X and Y Data

Pearson Correlation The Pearson (product-moment) correlation coefficient can be calculated for 2 continuous variables in a sample (regardless of distribution) using the formula:

Correlation Figures Y A B • • • • • • • ρ=0 No relationship D X • • C • • • ρ=1 • • ρ = -1 • • • Perfect positive relationship Perfect negative relationship • • • • • ρ = 0. 5 Moderate positive relationship E • • • • • ρ = -0. 8 • Strong negative relationship

Correlation Inference • Easy “large sample” test for H 0: ρ=0 For n ≥ 25, compute which has N(0, ) distribution under H 0 • This test assumes X, Y~ NBiv(μX, μY, σX 2, ρ) Many times a tenuous assumption! • Beware positive skewness & outliers • Beware data not truly continuous

Timeout: ASSUMPTIONS • As with any mathematical or physical model, model assumptions are critical to making the correct inference • Dealing with assumptions has lead to development of: – Nonparametric statistics: techniques that reduce or eliminate dependence on the underlying distribution of the data – Robust statistics: techniques that are affected little by departures from assumptions

Correlation (resumed) • A nonparametric version of the correlation coefficient: Spearman’s Rank Correlation • Like ρ, rs : – ranges from -1 to 1 – 0 no correlation, 1 perfect agreement – only requires ordinal data

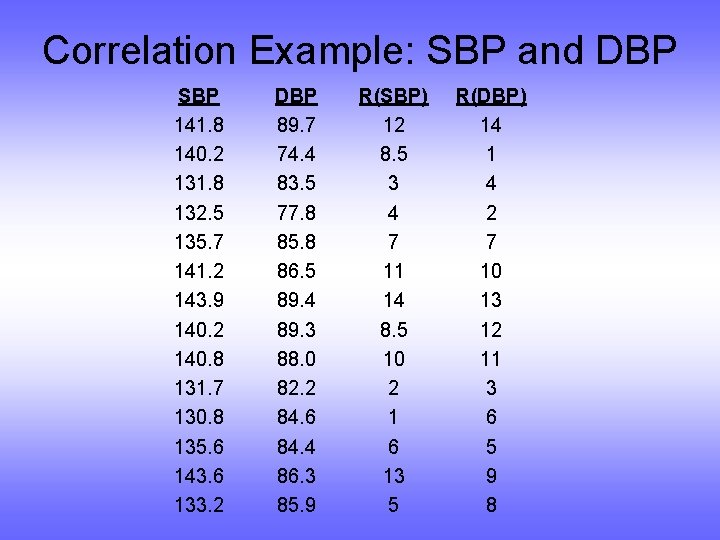
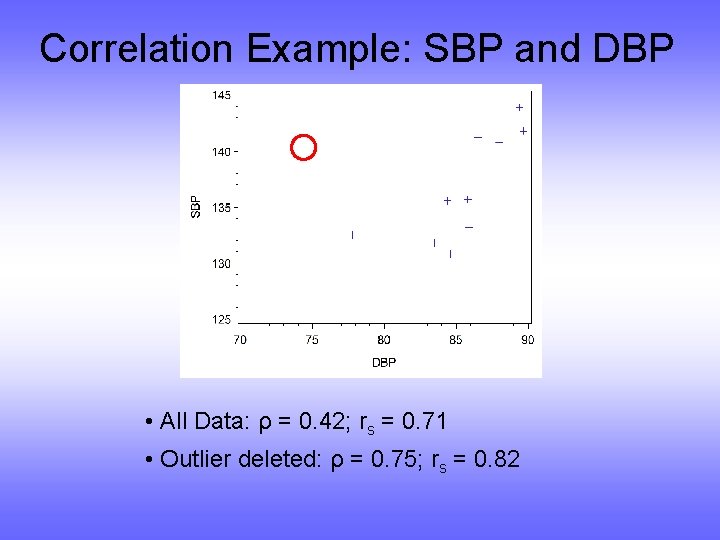
Correlation Example: SBP and DBP SBP 141. 8 140. 2 131. 8 132. 5 135. 7 141. 2 143. 9 140. 2 140. 8 131. 7 130. 8 135. 6 143. 6 133. 2 DBP 89. 7 74. 4 83. 5 77. 8 85. 8 86. 5 89. 4 89. 3 88. 0 82. 2 84. 6 84. 4 86. 3 85. 9 R(SBP) 12 8. 5 3 4 7 11 14 8. 5 10 2 1 6 13 5 R(DBP) 14 1 4 2 7 10 13 12 11 3 6 5 9 8

Correlation Example: SBP and DBP • All Data: ρ = 0. 42; rs = 0. 71 • Outlier deleted: ρ = 0. 75; rs = 0. 82

Correlation Coefficient Questions – 1. Can we calculate a correlation coefficient between the incomes of a group of people and what city they live in? No, we cannot, since city is a categorical variable. Correlation requires that both variables be quantitative.

Correlation Coefficient Questions – 2. Does it change the correlation between height and weight if we measure height in inches rather than centimeters and weight in pounds rather than kilograms? No. Because ρ (and r) uses the standardized values of the observations, ρ does not change when we change the units of measurements of x , y, or both. The correlation ρ itself has no unit of measure; it is just a number.

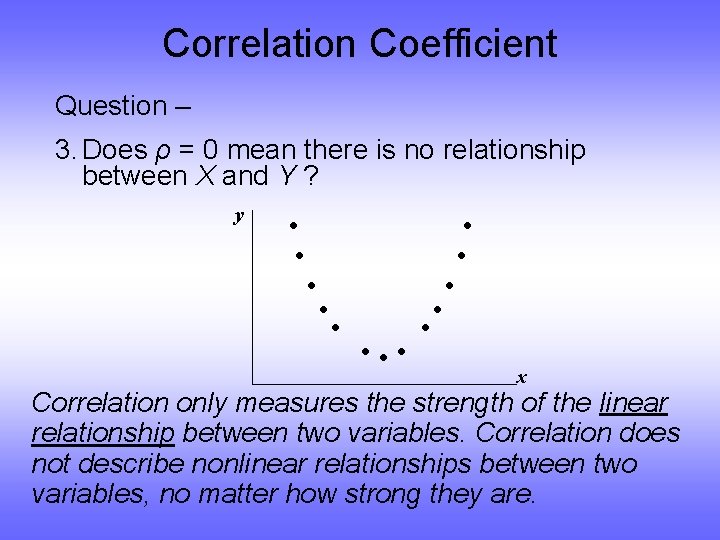
Correlation Coefficient Question – 3. Does ρ = 0 mean there is no relationship between X and Y ? y • • • • • • • x Correlation only measures the strength of the linear relationship between two variables. Correlation does not describe nonlinear relationships between two variables, no matter how strong they are.

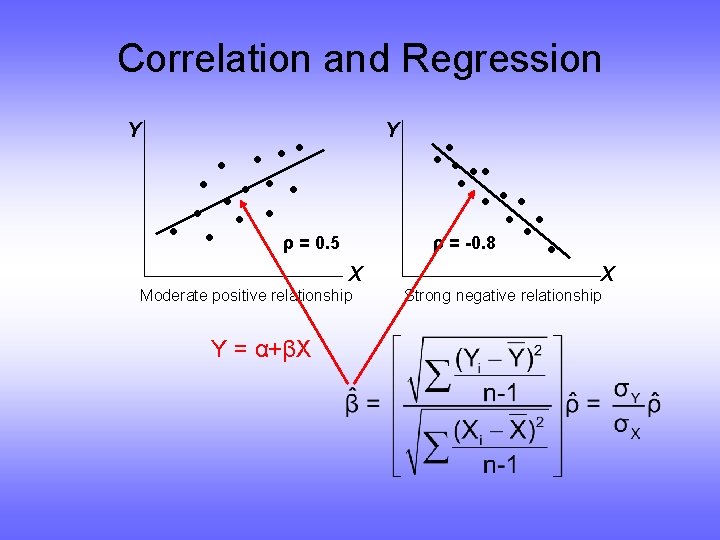
Correlation and Regression Y Y • • • • • ρ = 0. 5 X Moderate positive relationship Y = α+βX • • • • ρ = -0. 8 • X Strong negative relationship

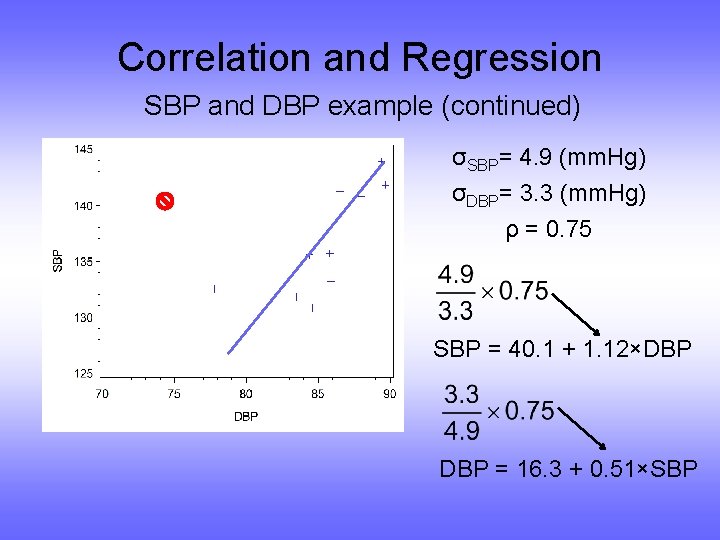
Correlation and Regression SBP and DBP example (continued) σSBP= 4. 9 (mm. Hg) σDBP= 3. 3 (mm. Hg) ρ = 0. 75 SBP = 40. 1 + 1. 12×DBP = 16. 3 + 0. 51×SBP

Correlation and Covariance • Suppose two random variables, X and Y: E(X) = μX, V(X) = σX 2; E(Y) = μY, V(Y) = σY 2; and Corr(X, Y) = ρ • Define Cov(X, Y) = E[(X-μX)(Y-μY)] Note: Cov(X, X) = E[(X-μX)(X-μx)] = E(X-μX)2 = σX 2 • Population correlation (ρ) is defined as: • Thus Cov(X, Y) = ρσXσY

Correlation and Covariance What’s the big deal about covariance? Use it to find the variance of functions of random variables, e. g. : In general:

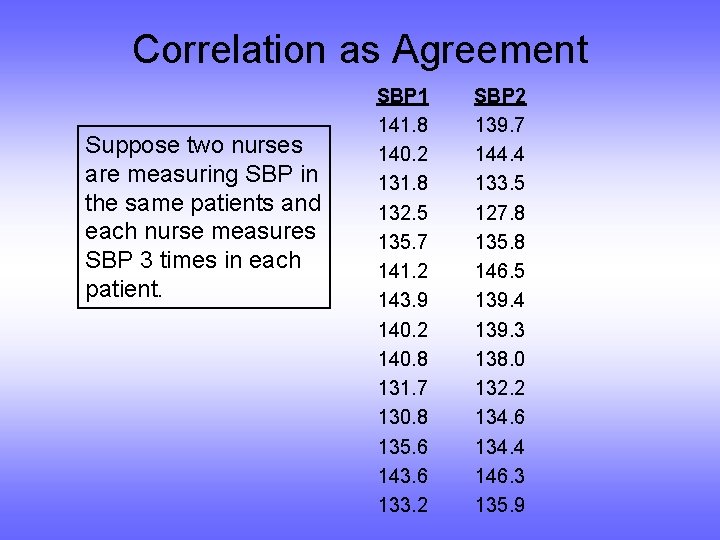
Correlation as Agreement Suppose two nurses are measuring SBP in the same patients and each nurse measures SBP 3 times in each patient. SBP 1 141. 8 140. 2 131. 8 132. 5 135. 7 141. 2 143. 9 140. 2 140. 8 131. 7 130. 8 135. 6 143. 6 133. 2 SBP 2 139. 7 144. 4 133. 5 127. 8 135. 8 146. 5 139. 4 139. 3 138. 0 132. 2 134. 6 134. 4 146. 3 135. 9

Correlation as Agreement • Could use Pearson correlation • Another measure, intraclass correlation – Can separate the variance into two sources: betweensubject and within-subject – The intraclass correlation is the ratio of the withinsubject to the total (i. e. , within + between) – By definition, intraclass correlation ranges from 0 to 1 – Best measure of the “individual” touch • In SBP example: ρ(Pearson) = 0. 809 ρ(Intraclass) = 0. 814

Things to Remember About Correlation • 5 warnings (adopted from Huck): 1. 2. 3. 4. Does not speak to cause-and-effect Beware outliers Assumes linear relationship Correlation vs. Independence § Zero correlation implies independence for Normal distribution only 5. Strength of relationship WRT trend

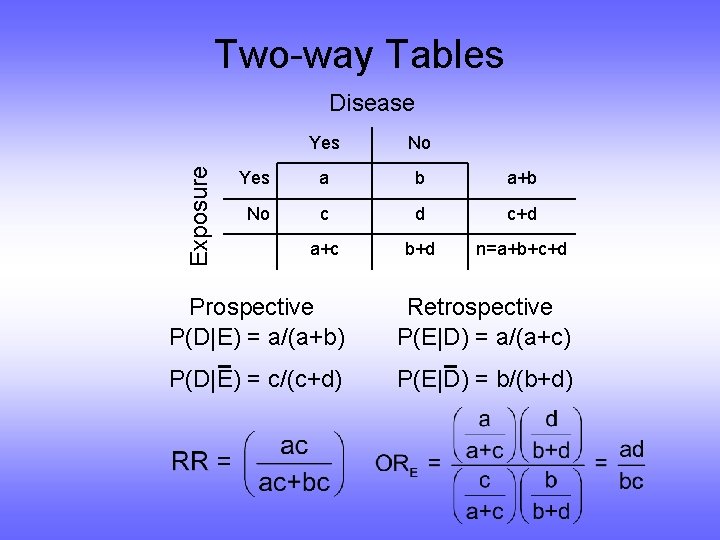
Categorical Outcomes: Two-way Tables • Prospective Design Relative Risk (RR) P(Disease in Exposed Group) P(D|E) = P(Disease in Unexposed Group) P(D|E) • Retrospective Design Odds Ratio (OR)

Two-way Tables Exposure Disease Yes No Yes a b a+b No c d c+d a+c b+d n=a+b+c+d Prospective P(D|E) = a/(a+b) Retrospective P(E|D) = a/(a+c) P(D|E) = c/(c+d) P(E|D) = b/(b+d)

Two-way Tables • Prospective design and relative risk (RR) are optimal • Retrospective designs and odds ratio (OR) are easiest (cheapest) • Can compute OR for prospective design

Two-way Table • Why we like the odds ratio… The exposure odds ratio is equivalent to the disease odds ratio! • Regardless of study design (i. e. , which margin is fixed) the estimate of the OR is the same

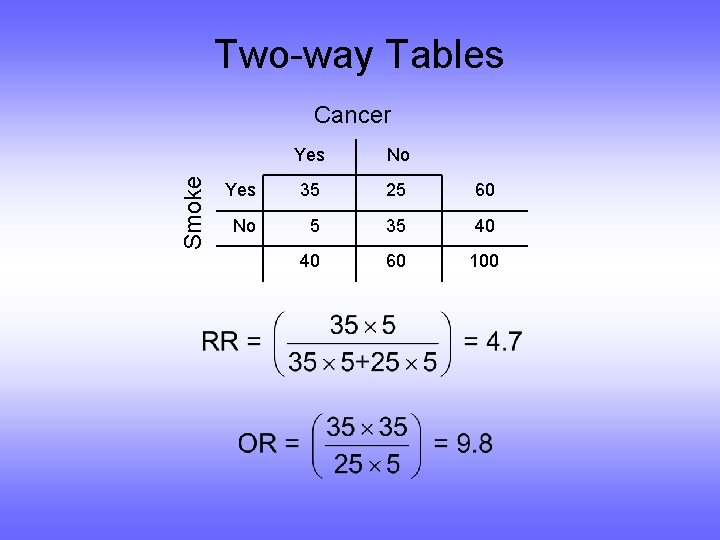
Two-way Tables Smoke Cancer Yes No Yes 35 25 60 No 5 35 40 40 60 100

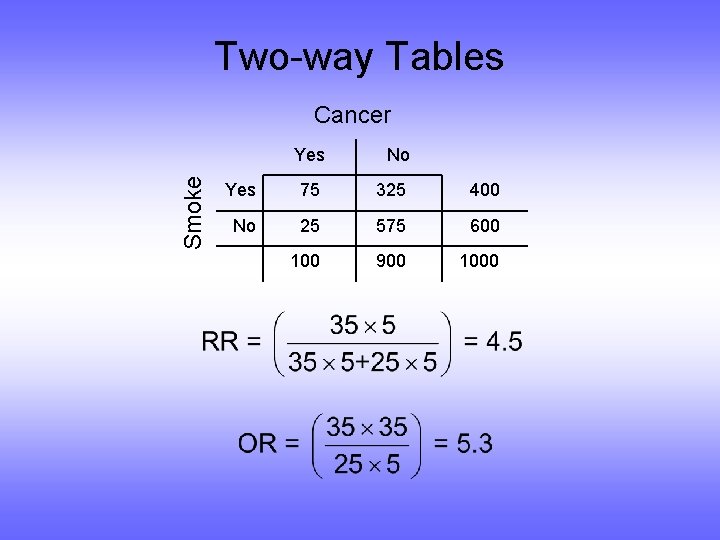
Two-way Table Why we like the odds ratio – Part II • For retrospective design, if… – Cases are representative of the population of all cases – Controls are representative of the population of all controls – The disease is “rare” (i. e. , prevalence <20%) Then OR ≈ RR

Two-way Tables Smoke Cancer Yes No Yes 75 325 400 No 25 575 600 100 900 1000

Other Measures From Clinical Trials Treatment Outcome Yes No Experimental 15 135 150 Control 100 150 250 115 285 400 P(O|E) = 15/150 = 0. 1 P(O|C) = 100/250 = 0. 4 RR = P(O|E)/P(O|C) = 0. 25 • Absolute Risk Reduction (ARR) = P(O|C) - P(O|E) = 0. 3 • Relative Risk Reduction (RRR) = 1 – RR = 0. 75 • Number Needed to Treat (NNT) = 1/ARR = 3. 33 (number needed to treat in the population to prevent 1 outcome event)

Things to Remember About Measures of Association 1. Beware: some sources use “odds ratio” and “relative risk” interchangeably – In most settings, OR overestimates RR 2. Be on guard when considering ARR, RRR, and NNT – Almost never see a SE or CI estimate – Should be based on large, well planned, prospective studies

Categorical Measures of Agreement • The “kappa” coefficient or κ • Example: two physicians diagnosing a disease DOCTOR A DOCTOR B Disease No Disease pa pb p. A No Disease pc pd q. A p. B q. B 1 Here pa, pb, pc, pd are the proportions of subjects, not the number of subjects.

Psychiatrist A Kappa Example Psychiatrist B Neurosis Normal Neurosis 0. 04 0. 06 0. 10 Normal 0. 01 0. 89 0. 90 0. 05 0. 95 1. 00 • Kappa is a categorical analog of the intraclass correlation • Kappa can be computed for any “square” (k×k) tables

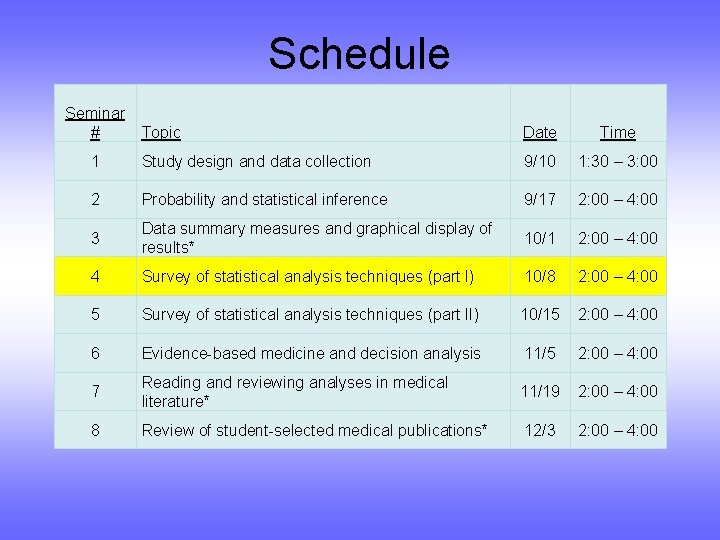
Schedule Seminar # Topic Date Time 1 Study design and data collection 9/10 1: 30 – 3: 00 2 Probability and statistical inference 9/17 2: 00 – 4: 00 3 Data summary measures and graphical display of results* 10/1 2: 00 – 4: 00 4 Survey of statistical analysis techniques (part I) 10/8 2: 00 – 4: 00 5 Survey of statistical analysis techniques (part II) 10/15 2: 00 – 4: 00 6 Evidence-based medicine and decision analysis 11/5 2: 00 – 4: 00 7 Reading and reviewing analyses in medical literature* 11/19 2: 00 – 4: 00 8 Review of student-selected medical publications* 12/3 2: 00 – 4: 00