Lecture 3 Computer Number System Number System The

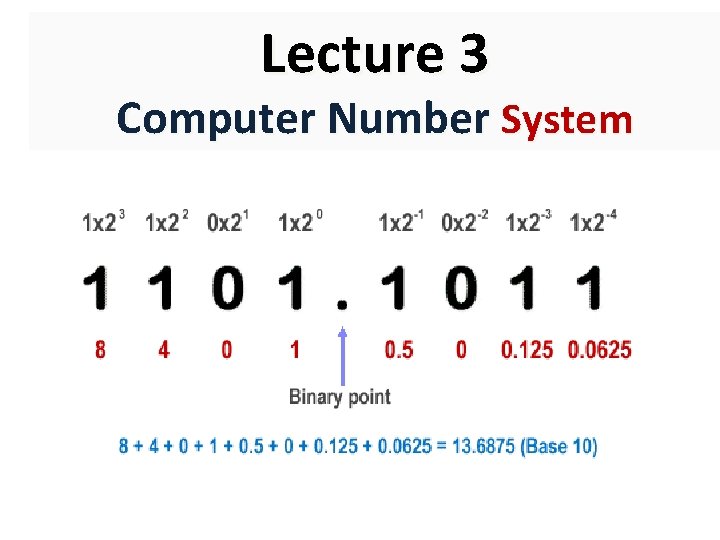
Lecture 3 Computer Number System

Number System The Binary Number System • To convert data into strings of numbers, computers use the binary number system. • Humans use the decimal system (“deci” stands for “ten”). • Elementary storage units inside computer are electronic switches. Each switch holds one of two states: on (1) or off (0). • • OFF ON We use a bit (binary digit), 0 or 1, to represent the state. The binary number system works the same way as the decimal system, but has only two available symbols (0 and 1) rather than ten (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9). 0 (00) 1 (01) 2 (10) 3 (11)

Number System Bits and Bytes • A single unit of data is called a bit, having a value of 1 or 0. • Computers work with collections of bits, grouping them to represent larger pieces of data, such as letters of the alphabet. • Eight bits make up one byte. A byte is the amount of memory needed to store one alphanumeric character. • With one byte, the computer can represent one of 256 different symbols or characters. 1 01 10 1 01 01

Common Number Systems System Base Symbols Decimal 10 0, 1, … 9 Binary 2 0, 1 Octal 8 0, 1, … 7 Hexadecimal 16 0, 1, … 9, A, B, … F

Quantities/Counting (1 of 2) Decimal 0 Hexa. Binary Octal decimal 0 0 0 1 2 1 10 1 2 3 4 5 6 7 11 100 101 110 111 3 4 5 6 7

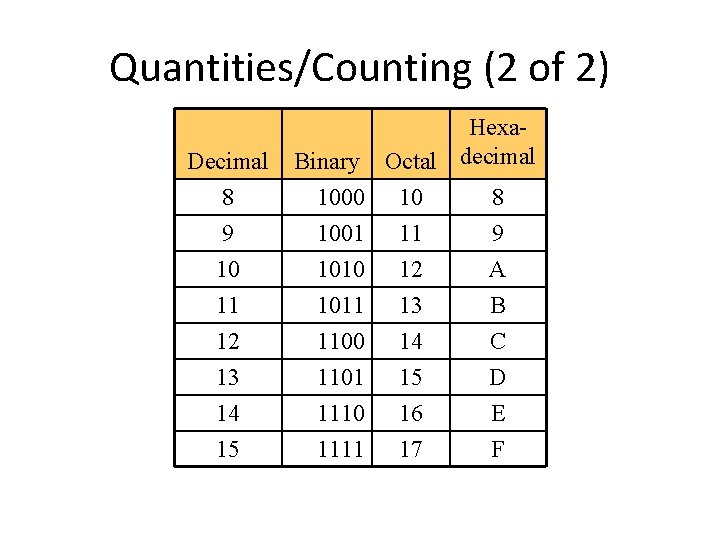
Quantities/Counting (2 of 2) Decimal 8 Hexa. Binary Octal decimal 1000 10 8 9 10 1001 1010 11 12 9 A 11 12 13 14 15 1011 1100 1101 1110 1111 13 14 15 16 17 B C D E F

Conversion Among Bases • The possibilities: Decimal Octal Binary Hexadecimal

Quick Example 2510 = 110012 = 318 = 1916 Base

Decimal to Decimal (just for fun) Decimal Octal Binary Hexadecimal Next slide…

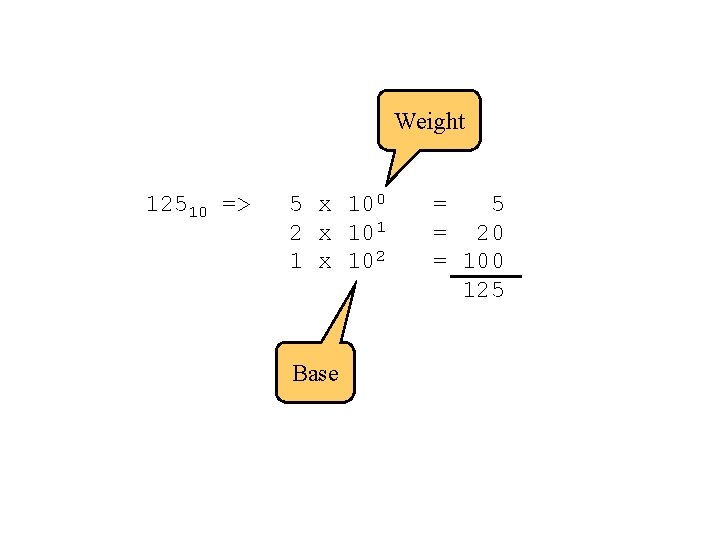
Weight 12510 => 5 x 100 2 x 101 1 x 102 Base = 5 = 20 = 100 125

Binary to Decimal Octal Binary Hexadecimal

Binary to Decimal • Technique – Multiply each bit by 2 n, where n is the “weight” of the bit – The weight is the position of the bit, starting from 0 on the right – Add the results

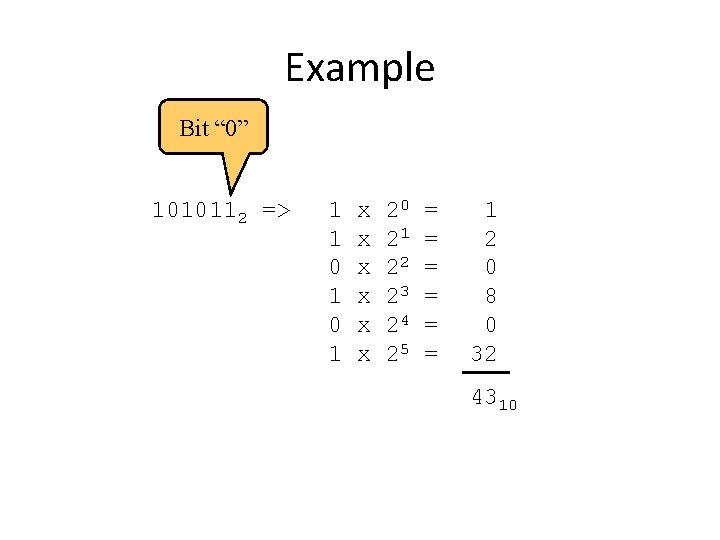
Example Bit “ 0” 1010112 => 1 1 0 1 x x x 20 21 22 23 24 25 = = = 1 2 0 8 0 32 4310

Octal to Decimal Octal Binary Hexadecimal

Octal to Decimal • Technique – Multiply each bit by 8 n, where n is the “weight” of the bit – The weight is the position of the bit, starting from 0 on the right – Add the results

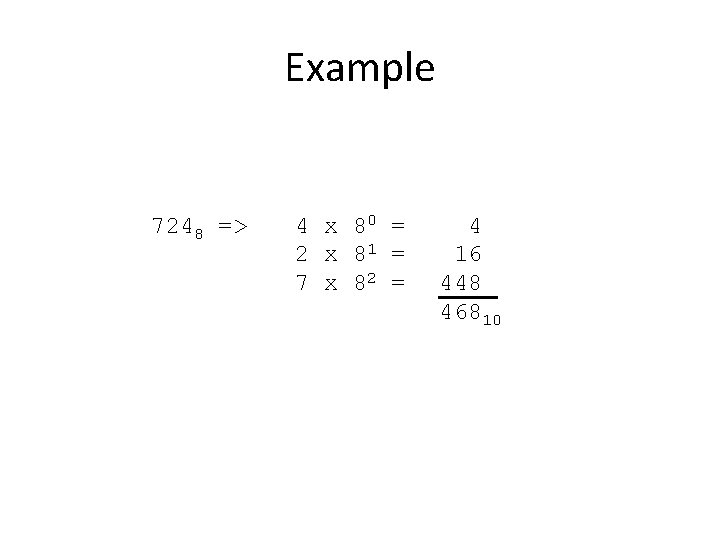
Example 7248 => 4 x 80 = 2 x 81 = 7 x 82 = 4 16 448 46810

Hexadecimal to Decimal Octal Binary Hexadecimal

Hexadecimal to Decimal • Technique – Multiply each bit by 16 n, where n is the “weight” of the bit – The weight is the position of the bit, starting from 0 on the right – Add the results

Example ABC 16 => C x 160 = 12 x 1 = 12 B x 161 = 11 x 16 = 176 A x 162 = 10 x 256 = 2560 274810

Decimal to Binary Decimal Octal Binary Hexadecimal

Decimal to Binary Repeated Division-by-2 Method )for whole number( To convert a whole number to binary, use successive division by 2 until the quotient is 0. The remainders form the answer, with the first remainder as the least significant bit (LSB) and the last as the most significant bit (MSB). (43)10 = (101011)2 Repeated Multiplication-by-2 Method (for fractions) To convert decimal fractions to binary, repeated multiplication by 2 is used, until the fractional product is 0 (or until the desired number of decimal places). The carried digits, or carries, produce the answer, with the first carry as the MSB, and the last as the LSB. (0. 3125)10 = (. 0101)2

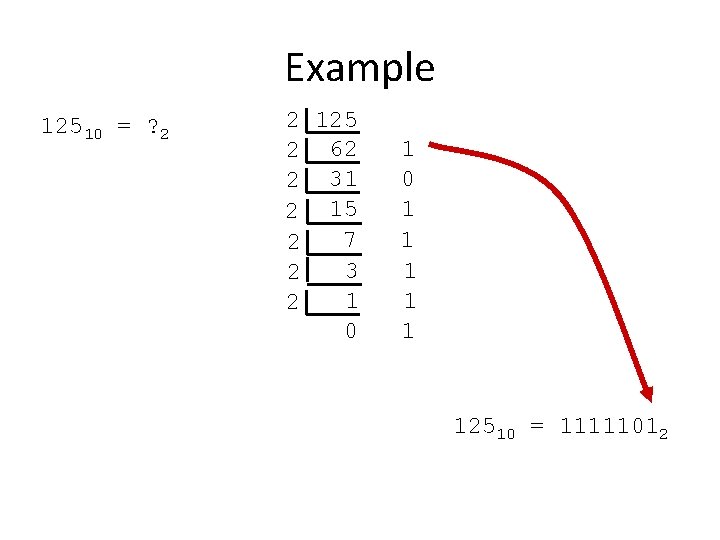
Example 12510 = ? 2 2 125 2 62 2 31 2 15 7 2 3 2 1 2 0 1 1 1 12510 = 11111012

Octal to Binary Decimal Octal Binary Hexadecimal

Octal to Binary • Technique – Convert each octal digit to a 3 -bit equivalent binary representation

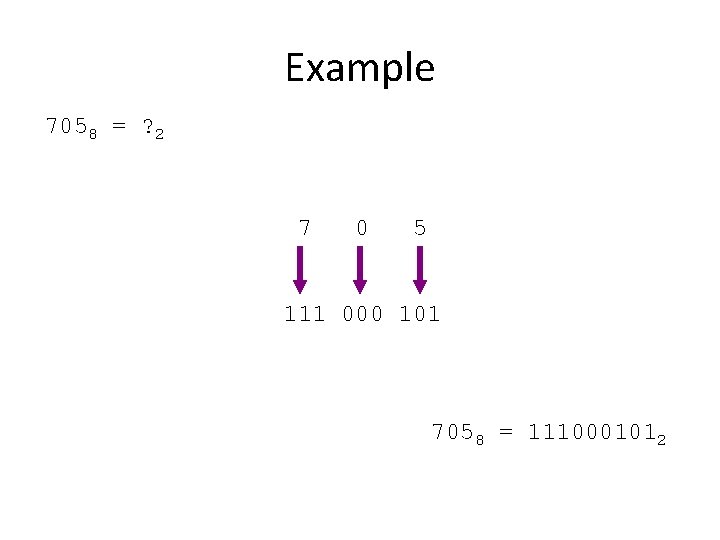
Example 7058 = ? 2 7 0 5 111 000 101 7058 = 1110001012

Hexadecimal to Binary Decimal Octal Binary Hexadecimal

Hexadecimal to Binary • Technique – Convert each hexadecimal digit to a 4 -bit equivalent binary representation

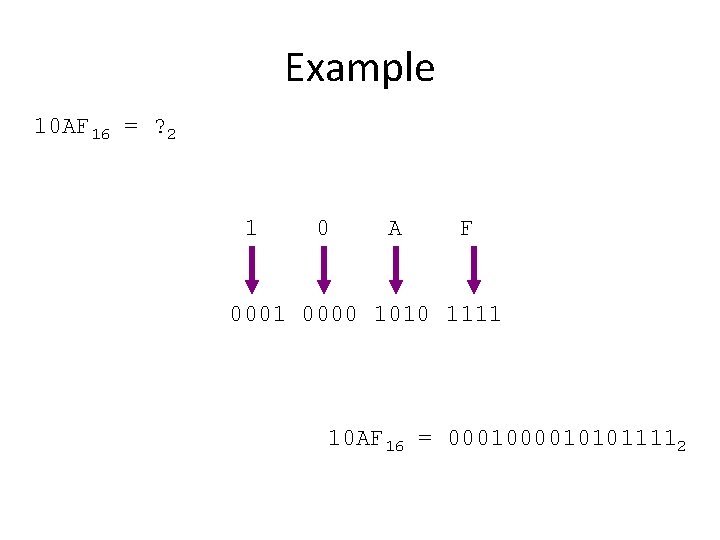
Example 10 AF 16 = ? 2 1 0 A F 0001 0000 1010 1111 10 AF 16 = 000101011112

Decimal to Octal Decimal Octal Binary Hexadecimal

Decimal to Octal • Technique – Divide by 8 – Keep track of the remainder

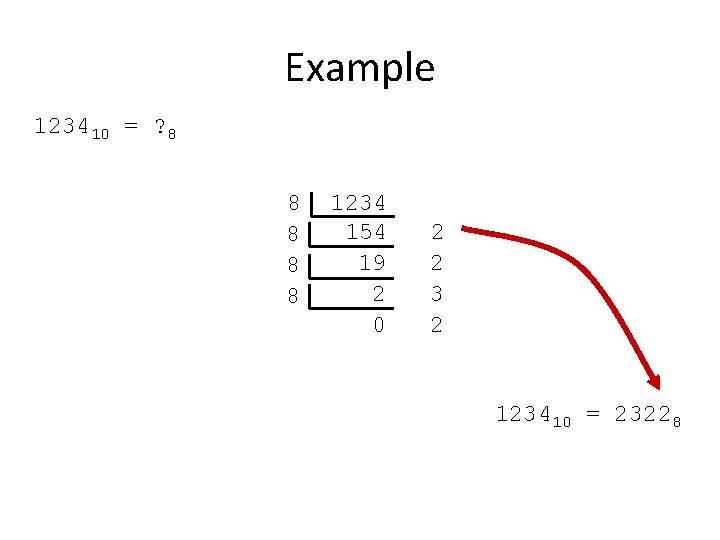
Example 123410 = ? 8 8 8 1234 154 19 2 0 2 2 3 2 123410 = 23228

Decimal to Hexadecimal Decimal Octal Binary Hexadecimal

Decimal to Hexadecimal • Technique – Divide by 16 – Keep track of the remainder

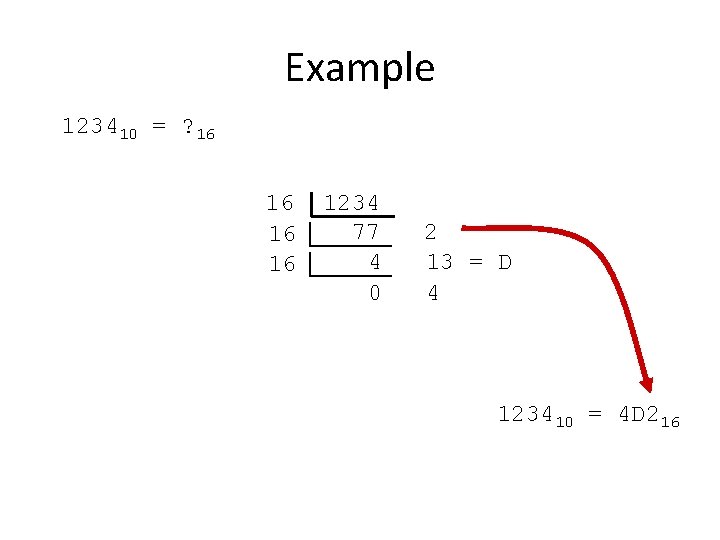
Example 123410 = ? 16 16 1234 77 4 0 2 13 = D 4 123410 = 4 D 216

Binary to Octal Decimal Octal Binary Hexadecimal

Binary to Octal • Technique – Group bits in threes, starting on right – Convert to octal digits

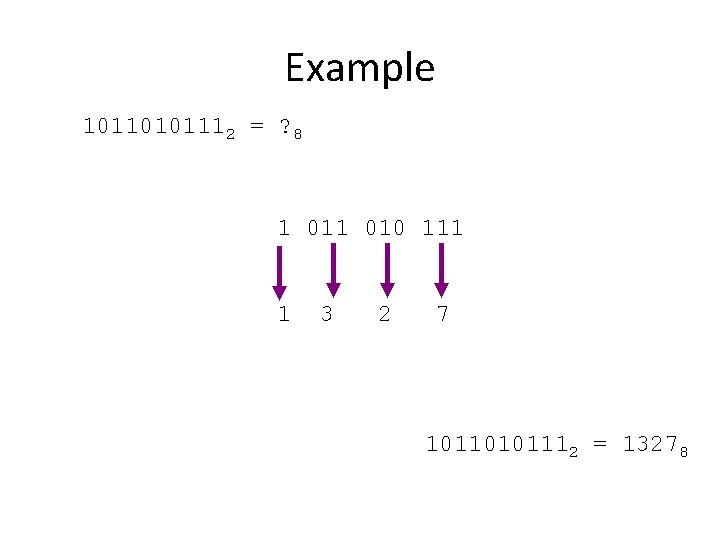
Example 10110101112 = ? 8 1 010 111 1 3 2 7 10110101112 = 13278

Binary to Hexadecimal Decimal Octal Binary Hexadecimal

Binary to Hexadecimal • Technique – Group bits in fours, starting on right – Convert to hexadecimal digits

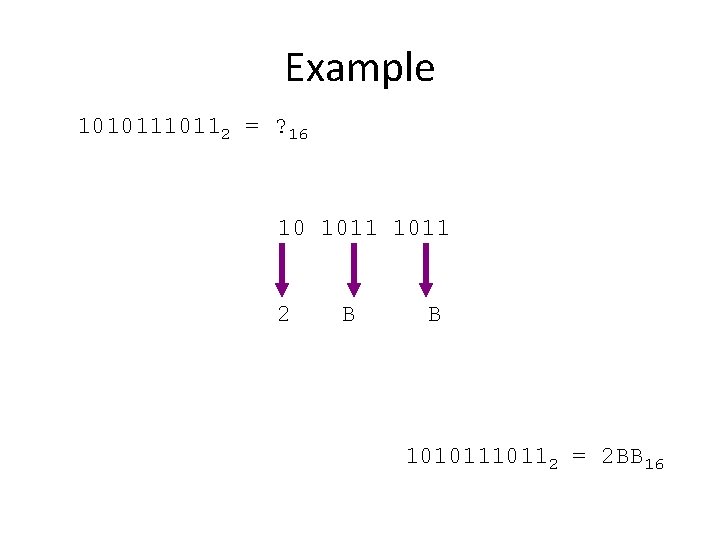
Example 1010112 = ? 16 10 1011 2 B B 1010112 = 2 BB 16

Octal to Hexadecimal Decimal Octal Binary Hexadecimal

Octal to Hexadecimal • Technique – Use binary as an intermediary

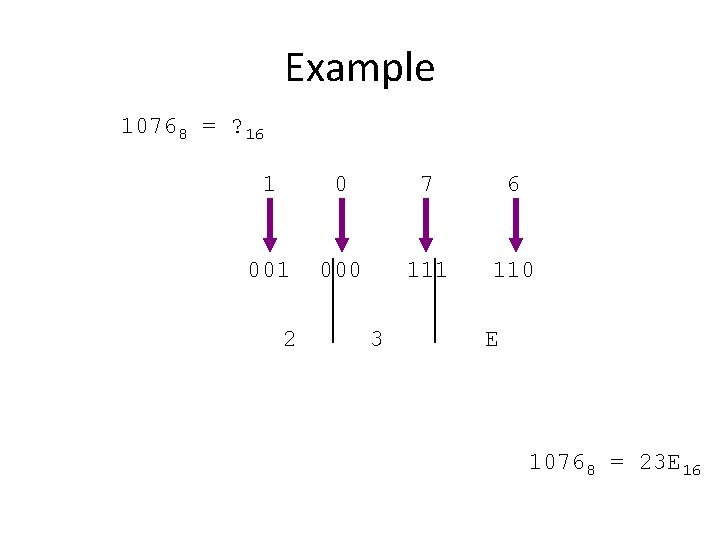
Example 10768 = ? 16 1 0 7 6 001 000 111 110 2 3 E 10768 = 23 E 16

Hexadecimal to Octal Decimal Octal Binary Hexadecimal

Hexadecimal to Octal • Technique – Use binary as an intermediary

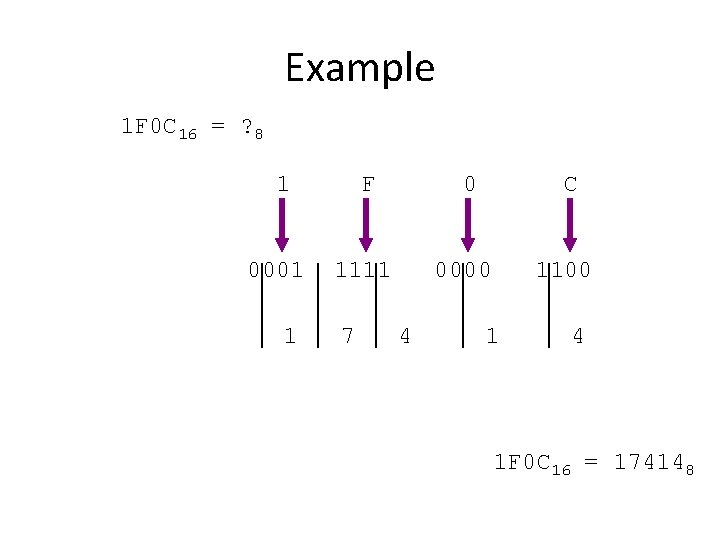
Example 1 F 0 C 16 = ? 8 1 0001 1 F 0 1111 7 C 0000 4 1100 1 4 1 F 0 C 16 = 174148

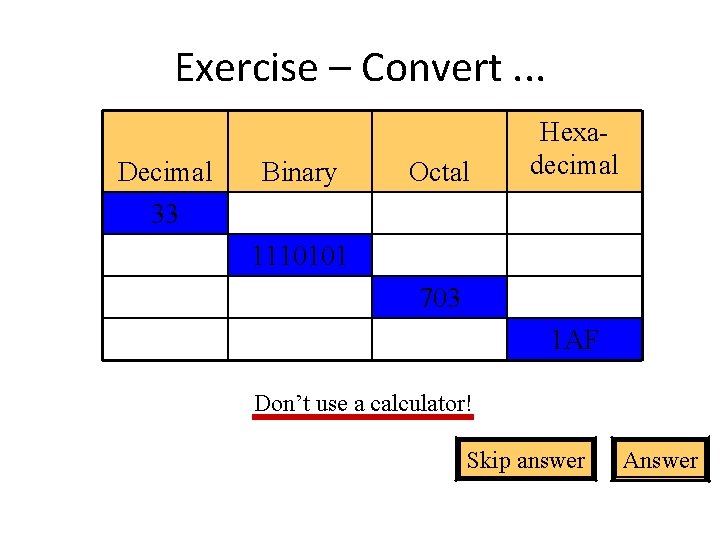
Exercise – Convert. . . Decimal 33 Binary Octal Hexadecimal 1110101 703 1 AF Don’t use a calculator! Skip answer Answer

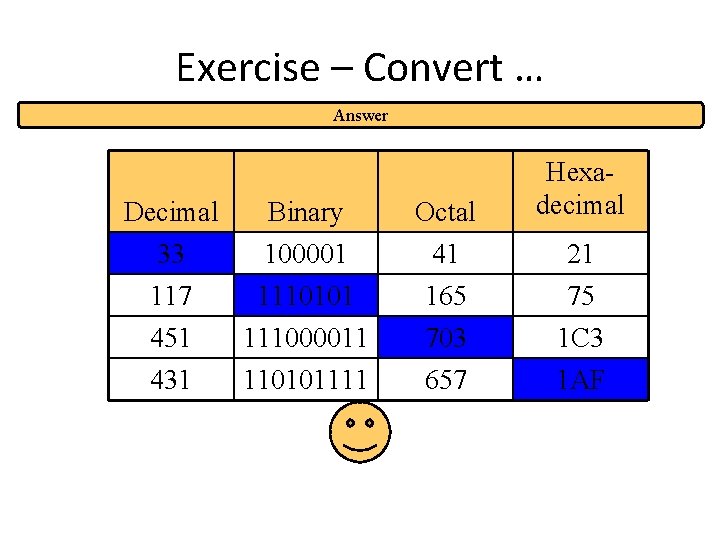
Exercise – Convert … Answer Decimal 33 117 Binary 100001 1110101 Octal 41 165 451 431 111000011 110101111 703 657 Hexadecimal 21 75 1 C 3 1 AF

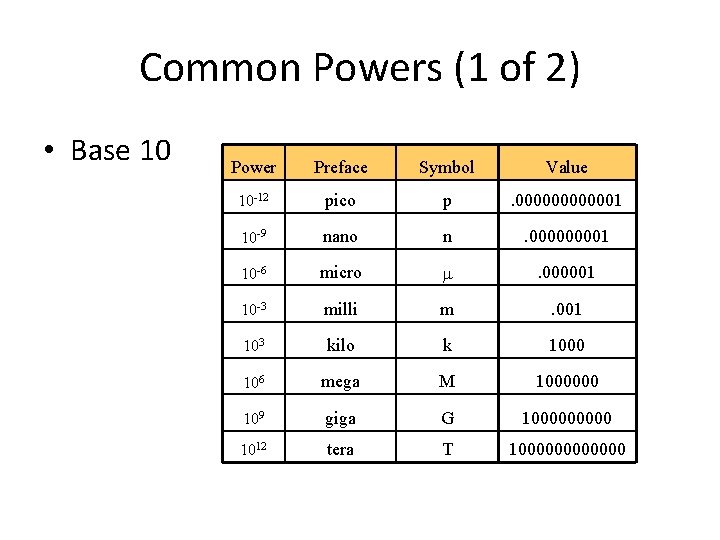
Common Powers (1 of 2) • Base 10 Power Preface Symbol Value 10 -12 pico p . 0000001 10 -9 nano n . 00001 10 -6 micro . 000001 10 -3 milli m . 001 103 kilo k 1000 106 mega M 1000000 109 giga G 100000 1012 tera T 1000000

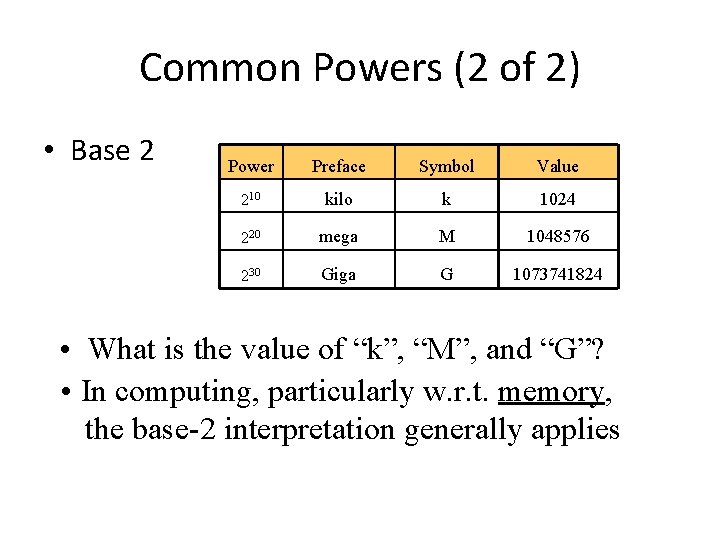
Common Powers (2 of 2) • Base 2 Power Preface Symbol Value 210 kilo k 1024 220 mega M 1048576 230 Giga G 1073741824 • What is the value of “k”, “M”, and “G”? • In computing, particularly w. r. t. memory, the base-2 interpretation generally applies

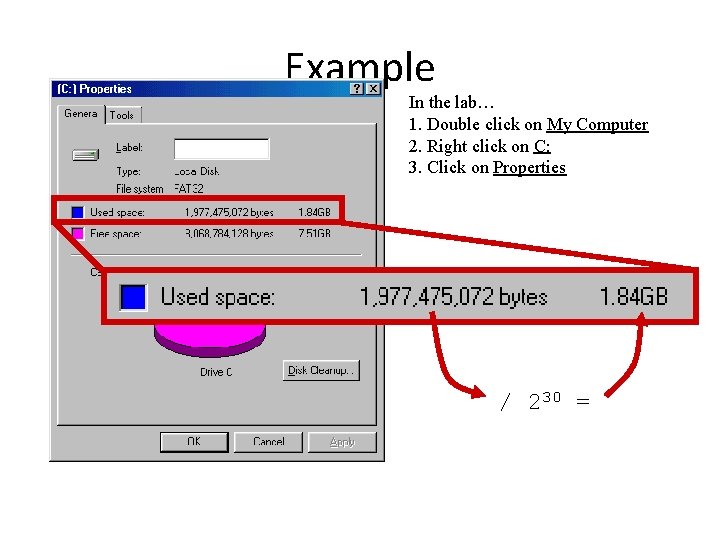
Example In the lab… 1. Double click on My Computer 2. Right click on C: 3. Click on Properties / 230 =

Exercise – Free Space • Determine the “free space” on all drives on a machine in the lab Free space Drive A: C: D: E: etc. Bytes GB

Review – multiplying powers • For common bases, add powers ab ac = ab+c 26 210 = 216 = 65, 536 or… 26 210 = 64 k

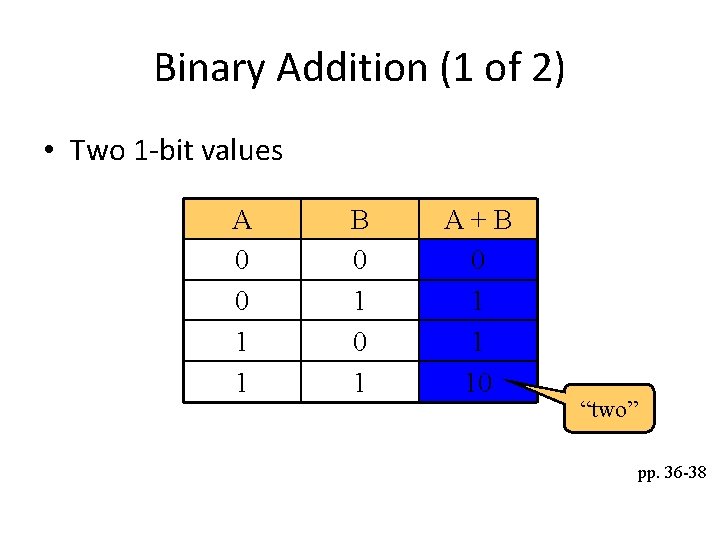
Binary Addition (1 of 2) • Two 1 -bit values A 0 0 1 1 B 0 1 A+B 0 1 1 10 “two” pp. 36 -38

Binary Addition (2 of 2) • Two n-bit values – Add individual bits – Propagate carries – E. g. , 1 1 10101 + 11001 101110 21 + 25 46

Multiplication (1 of 3) • Decimal (just for fun) 35 x 105 175 000 35 3675 pp. 39

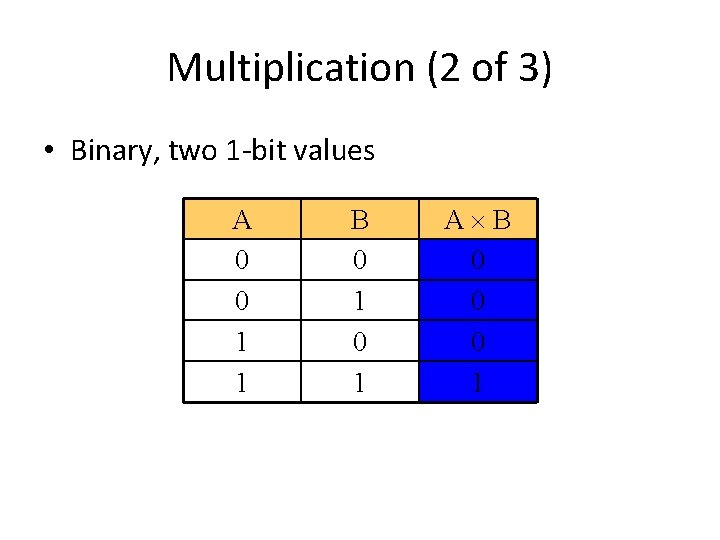
Multiplication (2 of 3) • Binary, two 1 -bit values A 0 0 1 1 B 0 1 A B 0 0 0 1

Multiplication (3 of 3) • Binary, two n-bit values – As with decimal values – E. g. , 1110 x 1011 1110 0000 1110 10011010

Fractions • Decimal to decimal (just for fun) 3. 14 => 4 x 10 -2 = 0. 04 1 x 10 -1 = 0. 1 3 x 100 = 3 3. 14 pp. 46 -50

Fractions • Binary to decimal 10. 1011 => 1 1 0 1 x x x 2 -4 2 -3 2 -2 2 -1 20 21 = = = 0. 0625 0. 125 0. 0 0. 5 0. 0 2. 6875 pp. 46 -50

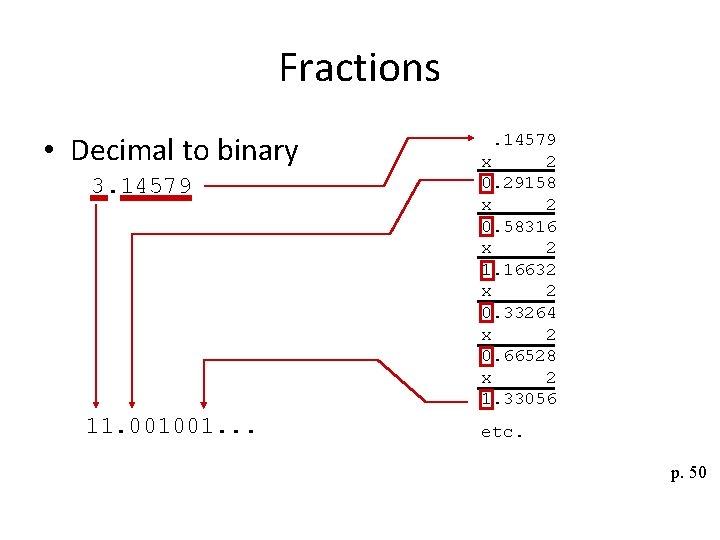
Fractions • Decimal to binary 3. 14579 11. 001001. . 14579 x 2 0. 29158 x 2 0. 58316 x 2 1. 16632 x 2 0. 33264 x 2 0. 66528 x 2 1. 33056 etc. p. 50

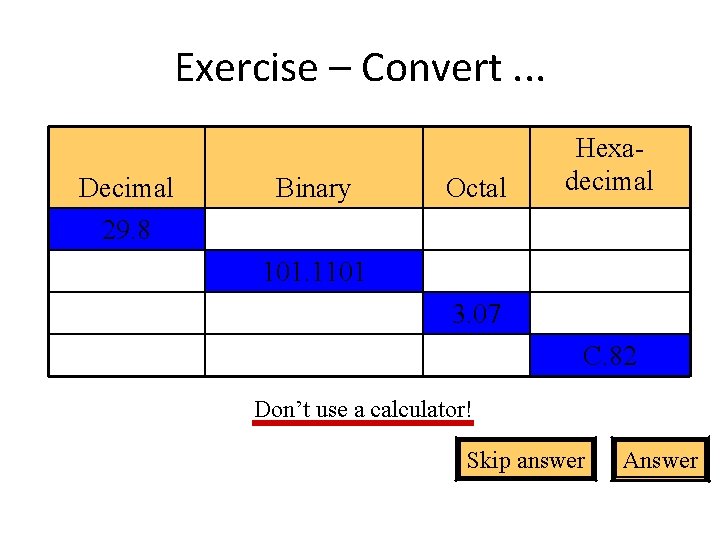
Exercise – Convert. . . Decimal 29. 8 Binary Octal Hexadecimal 101. 1101 3. 07 C. 82 Don’t use a calculator! Skip answer Answer

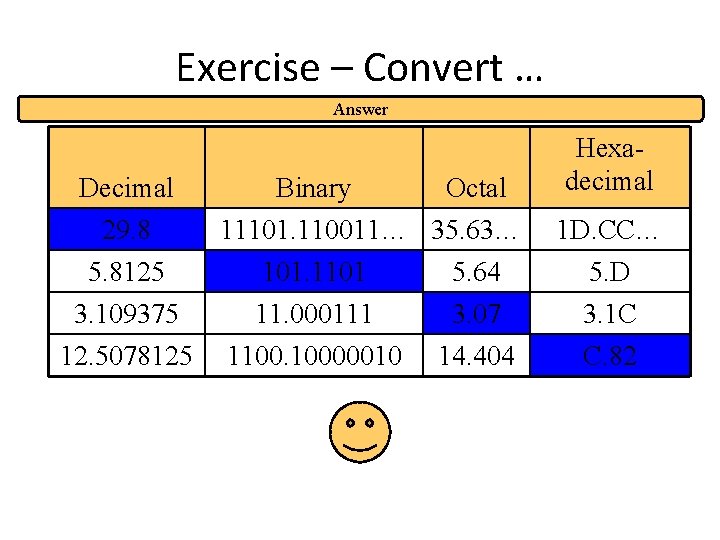
Exercise – Convert … Answer Decimal 29. 8 5. 8125 3. 109375 12. 5078125 Binary Octal 11101. 110011… 35. 63… 101. 1101 5. 64 11. 000111 1100. 10000010 3. 07 14. 404 Hexadecimal 1 D. CC… 5. D 3. 1 C C. 82

Thank you