Lecture 3 Chapter 19 Cont Electric Charges Forces

Lecture 3: Chapter 19 Cont Electric Charges, Forces and Electric Fields

Agenda n n n Compare the electric force to Gravitational force Superposition of forces Electric Field Superposition of Electric Field Shielding and Charging by Induction Electric Flux and Gauss’s Law

What did we study last lesson? Electric Charges: positive and neg. Electron (neg) and proton (pos) n Charges are conserved n Polarization n Insulators & Conductors n Coulomb’s Law n

Recap n Two rods and a cat fur: n Glass Rod (positive charges) n Rubber Rod (negative)

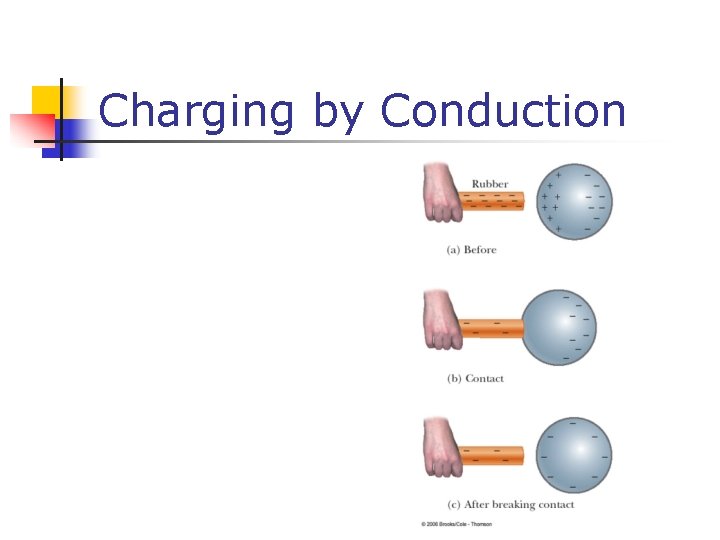
Charging by Conduction

Recap n n Coulomb’s Law (electrostatic force between point charges)

Recap n n n 7 Polarization is realignment of charge within individual molecules. Produces induced charge on the surface of insulators. how e. g. rubber or glass can be used to supply electrons.

Student Discussion A positively charged object hanging from a string is brought near a non conducting object (ball). The ball is seen to be attracted to the object. 1. Explain why it is not possible to determine whether the object is negatively charged or neutral. 2. What additional experiment is needed to reveal the electrical charge state of the object? ? 8 +

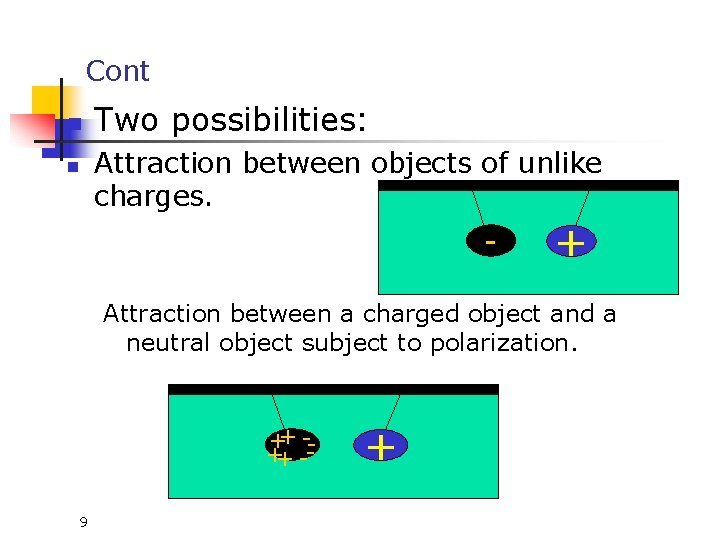
Cont n n Two possibilities: Attraction between objects of unlike charges. - + Attraction between a charged object and a neutral object subject to polarization. ++ -9 +

What additional experiment is needed to reveal the electrical charge state of the object? n Two Experiments: n Bring known neutral ball near the object and observe whethere is an attraction. ? 0 Bring a known negatively charge object near the first one. If there is an attraction, the object is neutral, and the attraction is achieved by polarization. +-+ + -+-+ 10 -

Question n Name the first action at a distance force you have encountered in physics so far. Electric Force 11

Electrical Forces are Field Forces n This is the second example of a field force n n n Gravity was the first Remember, with a field force, the force is exerted by one object on another object even though there is no physical contact between them There are some important similarities and differences between electrical and gravitational forces

Electrical Force Compared to Gravitational Force n n Both are inverse square laws The mathematical form of both laws is the same n n Masses replaced by charges G replaced by ke Electrical forces can be either attractive or repulsive Gravitational forces are always attractive

Example: Student Participation Consider a proton (mp=1. 67 x 10 -27 kg; qp=+1. 60 x 10 -19 C) and an electron (me=9. 11 x 10 -31 kg; qe=-1. 60 x 10 -19 C) separated by 5. 29 x 10 -11 m. The particles are attracted to each other by both the force of gravity and by Coulomb’s law force. Which of these has the larger magnitude? A. Gravitational force B. Coulomb’s law force 14

Which of these has the larger magnitude? A. Gravitational force B. Coulomb’s law force We will mostly ignore consider electrostatics. Pg. 659. By what factor the electric gravitational effects when force is greater than the gravitational force? we 15

Problem solving steps 1. Visualize problem – labeling variables 2. Determine which basic physical principle(s) apply 3. Write down the appropriate equations using the variables defined in step 1. 4. Check whether you have the correct amount of information to solve the problem (same number of knowns and unknowns). 5. Solve the equations. 6. Check whether your answer makes sense (units, order of magnitude, etc. ). 16

Superposition Principle n n From observations: one finds that whenever multiple charges are present, the net force on a given charge is the vector sum of all forces exerted by other charges. Electric force obeys a superposition principle. 17

The Superposition Principle n How to work the problem? n n Find the electrical forces between pairs of charges separately Then add the vectors n Remember to add the forces as vectors

Superposition Principle Example: 3 charges in a line F 12 F 13 q 1 = 6. 00 u. C q 2 = 1. 50 u. C q 3 = -2. 00 u. C d 1 = 3. 00 cm d 2 = 2. 00 cm K = 8. 99 x 109 N. m 2 /C 2 19

Example: Superposition Principle (Not along a line) Consider three point charges at the corners of a triangle, as shown in the next slide. Find the resultant force on q 3 if q 1 = 6. 00 x 10 -9 C q 2 = -2. 00 x 10 -9 C q 3 = 5. 00 x 10 -9 C 20

Superposition Principle Example n n n The force exerted by q 1 on q 3 is The force exerted by q 2 on q 3 is The total force exerted on q 3 is the vector sum of and

Consider three point charges at the corners of a triangle, as shown below. Find the resultant force on q 3. Solution: 12/1/2020 22

n n Spherical Charge Distribution Students need to read and work on pg 663/664

Electric Field - Discovery n n 24 Electric forces act through space even in the absence of physical contact. Suggests the notion of electrical field (first introduced by Michael Faraday (1791 -1867). 12/1/2020

Electric Field n n 25 An electric field is said to exist in a region of space surrounding a charged object. If another charged object enters a region where an electrical field is present, it will be subject to an electrical force. 12/1/2020

Electric Field n n n A charged particle, with charge Q, produces an electric field in the region of space around it A small test charge, qo, placed in the field, will experience a force. “The electric field is the force per charge at a given location”

Electric Field n Mathematically, n SI units are N / C Given: One finds:

Electric Field n Use this for the magnitude of the field n The electric field is a vector quantity n The direction of the field is defined to be the direction of the electric force that would be exerted on a small positive test charge placed at that point

Direction of Electric Field n The electric field produced by a negative charge is directed toward the charge n A positive test charge would be attracted to the negative source charge

Direction of Electric Field, cont n The electric field produced by a positive charge is directed away from the charge n A positive test charge would be repelled from the positive source charge

More About a Test Charge and The Electric Field n The test charge is required to be a small charge n n n It can cause no rearrangement of the charges on the source charge The electric field exists whether or not there is a test charge present The Superposition Principle can be applied to the electric field if a group of charges is present

Electric Fields and Superposition Principle n The superposition principle holds when calculating the electric field due to a group of charges n n n Find the fields due to the individual charges Add them as vectors Use symmetry whenever possible to simplify the problem

Electric Field, final

Problem Solving Strategy n n Draw a diagram of the charges in the problem Identify the charge of interest n n You may want to circle it Units – Convert all units to SI n Need to be consistent with ke

Problem Solving Strategy, cont n Apply Coulomb’s Law n n n Sum all the x- and y- components n n For each charge, find the force on the charge of interest Determine the direction of the force This gives the x- and y-components of the resultant force Find the resultant force by using the Pythagorean theorem and trig

Problem Solving Strategy, Electric Fields n Calculate Electric Fields of point charges n n n Use the equation to find the electric field due to the individual charges The direction is given by the direction of the force on a positive test charge The Superposition Principle can be applied if more than one charge is present

Examples of Electric Field a) b) c) E will be constant (a charged plane) E will decrease with distance as (a point charge) E in a line charge, decrease with a distance 1/r

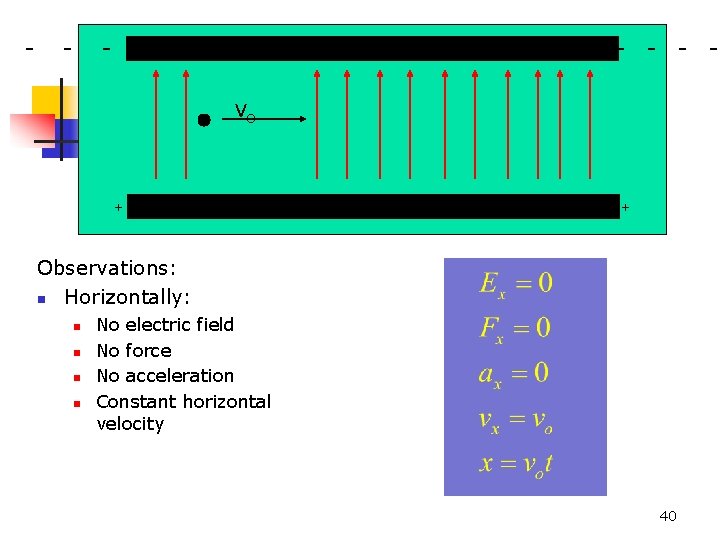
Example: n - - An electron moving horizontally passes between two horizontal planes, the upper plane charged negatively, and the lower positively. - - - - - vo - + 38 + + + + + + 12/1/2020

Example: n - - A uniform, upward-directed electric field exists in this region. This field exerts a force on the electron. Describe the motion of the electron in this region. - - - - - vo - + 39 + + + + + + 12/1/2020

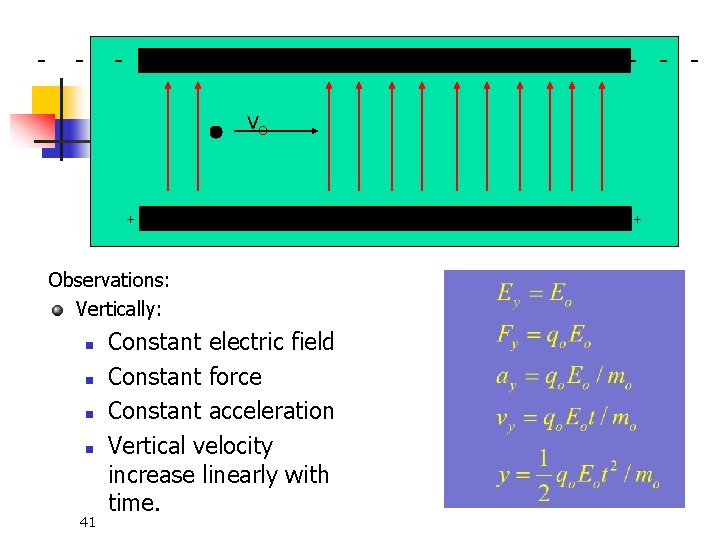
- - - - - - vo - + + + + + + Observations: n Horizontally: n n No electric field No force No acceleration Constant horizontal velocity 40

- - - - - vo - + + + + + + Observations: Vertically: n n 41 Constant electric field Constant force Constant acceleration Vertical velocity increase linearly with time.

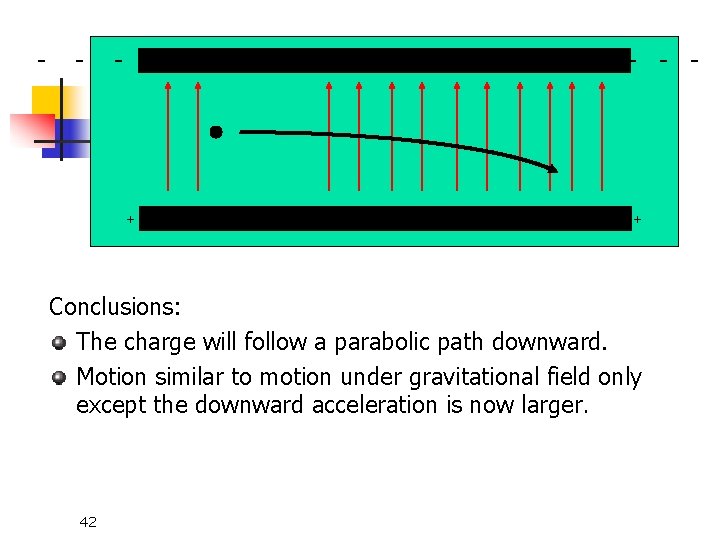
- - - - - - + + + + + + Conclusions: The charge will follow a parabolic path downward. Motion similar to motion under gravitational field only except the downward acceleration is now larger. 42

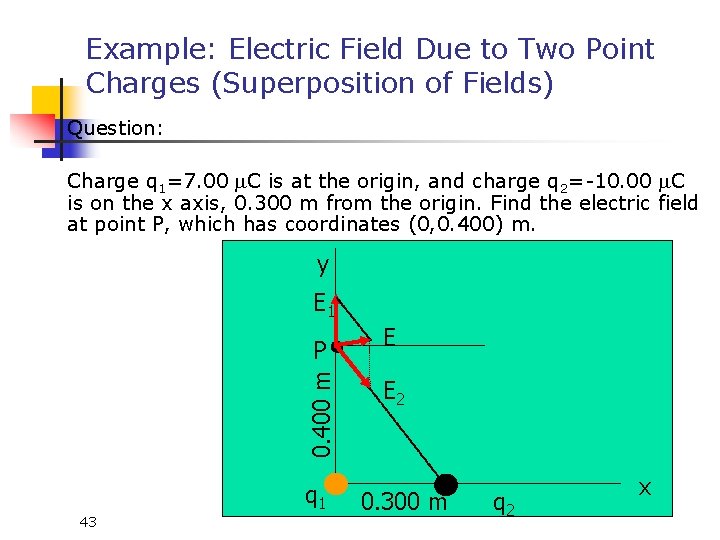
Example: Electric Field Due to Two Point Charges (Superposition of Fields) Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. y E 1 0. 400 m P q 1 43 E E 2 0. 300 m q 2 x

Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. Observations: n n n First find the Electric field at point P due to charge q 1 and q 2. Field E 1 at P due to q 1 is vertically upward. Field E 2 at due to q 2 is directed towards q 2. The net field at point P is the vector sum of E 1 and E 2. The magnitude is obtained with 44

Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. Set up the problem: q 1=7. 00 m. C q 2=-10. 00 m. C K = 8. 99 x 109 N. m 2 /C 2 r 1 = 0. 400 m r 2= ? What do we do? 45

Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. 1) Calculate r 2 2) Calculate the electric field at P 3) 46 I will work set it up, but you will need to finish (it looks like example in pg. 669)

Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. Solution: 47

Electric Field Lines n n A convenient aid for visualizing electric field patterns is to draw lines pointing in the direction of the field vector at any point These are called electric field lines and were introduced by Michael Faraday

Electric Field Lines, cont. n The field lines are related to the field in the following manners: n n The electric field vector, , is tangent to the electric field lines at each point The number of lines per unit area through a surface perpendicular to the lines is proportional to the strength of the electric field in a given region

Electric Field Line Patterns n n n Point charge The lines radiate equally in all directions For a positive source charge, the lines will radiate outward

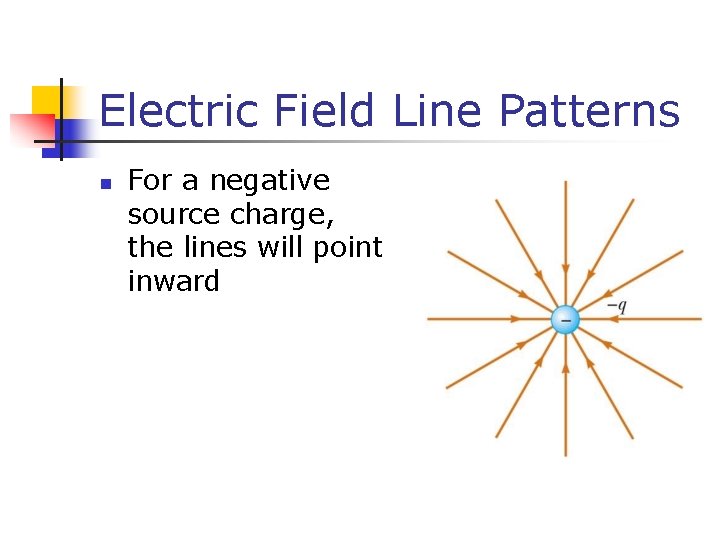
Electric Field Line Patterns n For a negative source charge, the lines will point inward

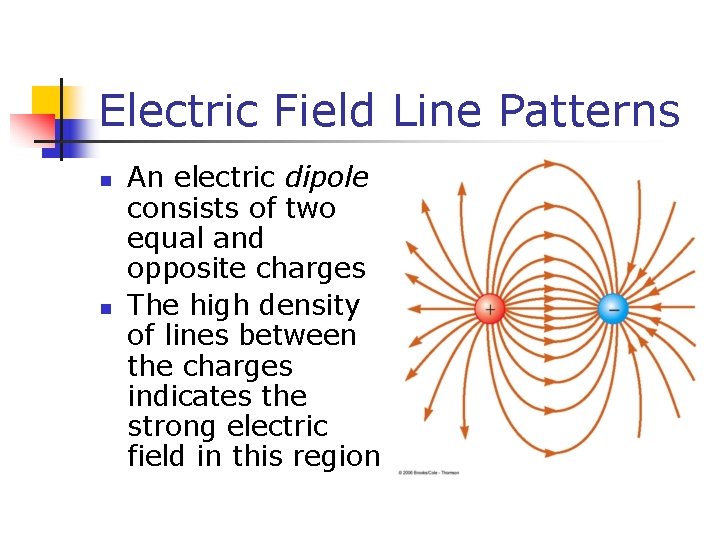
Electric Field Line Patterns n n An electric dipole consists of two equal and opposite charges The high density of lines between the charges indicates the strong electric field in this region

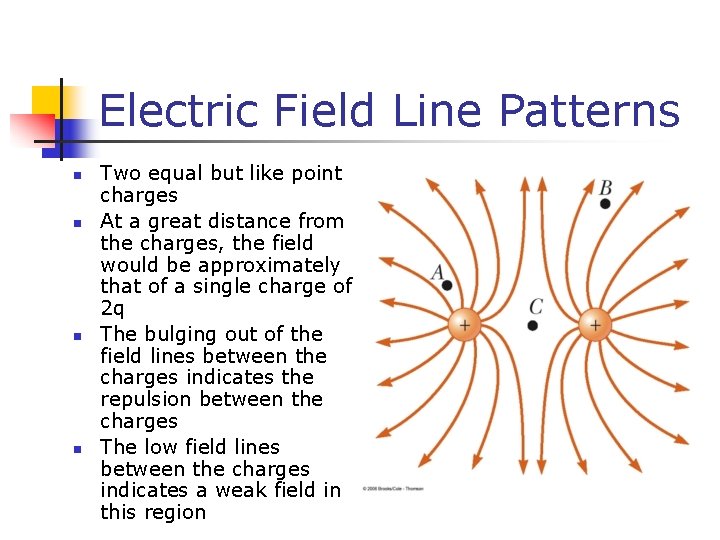
Electric Field Line Patterns n n Two equal but like point charges At a great distance from the charges, the field would be approximately that of a single charge of 2 q The bulging out of the field lines between the charges indicates the repulsion between the charges The low field lines between the charges indicates a weak field in this region

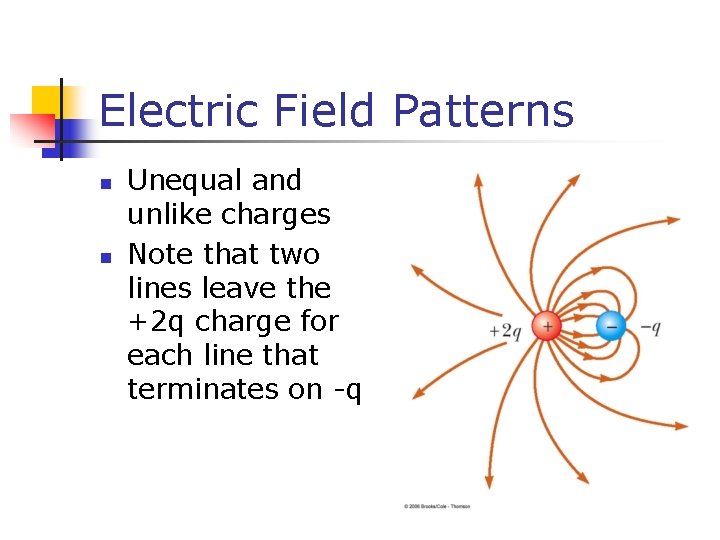
Electric Field Patterns n n Unequal and unlike charges Note that two lines leave the +2 q charge for each line that terminates on -q

Rules for Drawing Electric Field Lines n The lines for a group of charges must begin on positive charges and end on negative charges n n n In the case of an excess of charge, some lines will begin or end infinitely far away The number of lines drawn leaving a positive charge or ending on a negative charge is proportional to the magnitude of the charge No two field lines can cross each other

Electric Field Lines, final n n n The electric field lines are not material objects They are used only as a pictorial representation of the electric field at various locations They generally do not represent the path of a charged particle released in the electric field

Mini-Discussion Question: Is it safe to stay inside an automobile during a lightning storm? Why? 57

Question: Is it safe to stay inside an automobile during a lightning storm? Why? Answer: Yes. It is. The metal body of the carries the excess charges on its external surface. Occupants touching the inner surface are in no danger. SAFE 58 12/1/2020

Shielding and Charging by Induction n n When no net motion of charge occurs within a conductor, the conductor is said to be in electrostatic equilibrium An isolated conductor has the following properties: n n The electric field is zero everywhere inside the conducting material Any excess charge on an isolated conductor resides entirely on its surface

Properties, cont n n The electric field just outside a charged conductor is perpendicular to the conductor’s surface On an irregularly shaped conductor, the charge accumulates at locations where the radius of curvature of the surface is smallest (that is, at sharp points)

Property 1 n The electric field is zero everywhere inside the conducting material n Consider if this were not true n n If there were an electric field inside the conductor, the free charge there would move and there would be a flow of charge If there were a movement of charge, the conductor would not be in equilibrium

Property 2 n Any excess charge on an isolated conductor resides entirely on its surface n n A direct result of the 1/r 2 repulsion between like charges in Coulomb’s Law If some excess of charge could be placed inside the conductor, the repulsive forces would push them as far apart as possible, causing them to migrate to the surface

Property 3, cont. n n n Any excess charge moves to its surface The charges move apart until an equilibrium is achieved The amount of charge per unit area is greater at the flat end The forces from the charges at the sharp end produce a larger resultant force away from the surface Why a lightning rod works

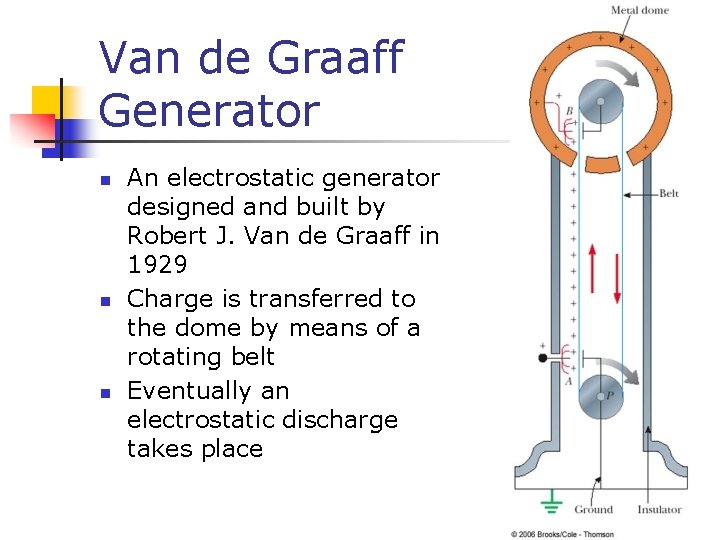
Van de Graaff Generator n n n An electrostatic generator designed and built by Robert J. Van de Graaff in 1929 Charge is transferred to the dome by means of a rotating belt Eventually an electrostatic discharge takes place

Electric Flux n n n Field lines penetrating an area A perpendicular to the field The product of EA is the flux, Φ In general: n ΦE = E A cos θ

Electric Flux, cont. n ΦE = E A cos θ n n The perpendicular to the area A is at an angle θ to the field When the area is constructed such that a closed surface is formed, use the convention that flux lines passing into the interior of the volume are negative and those passing out of the interior of the volume are positive

Gauss’ Law n Gauss’ Law states that the electric flux through any closed surface is equal to the net charge Q inside the surface divided by εo n n εo is the permittivity of free space and equals 8. 85 x 10 -12 C 2/Nm 2 The area in Φ is an imaginary surface, a Gaussian surface, it does not have to coincide with the surface of a physical object

Electric Field of a Charged Thin Spherical Shell n n The calculation of the field outside the shell is identical to that of a point charge The electric field inside the shell is zero

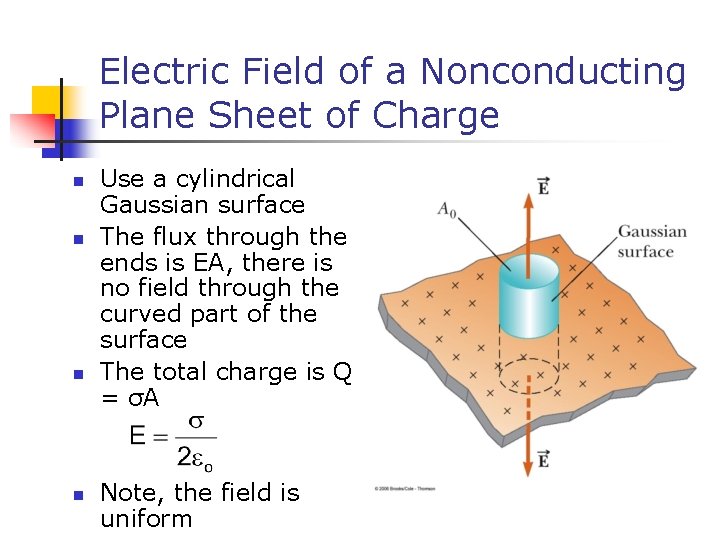
Electric Field of a Nonconducting Plane Sheet of Charge n n Use a cylindrical Gaussian surface The flux through the ends is EA, there is no field through the curved part of the surface The total charge is Q = σA Note, the field is uniform

Electric Field of a Nonconducting Plane Sheet of Charge, cont. n n The field must be perpendicular to the sheet The field is directed either toward or away from the sheet

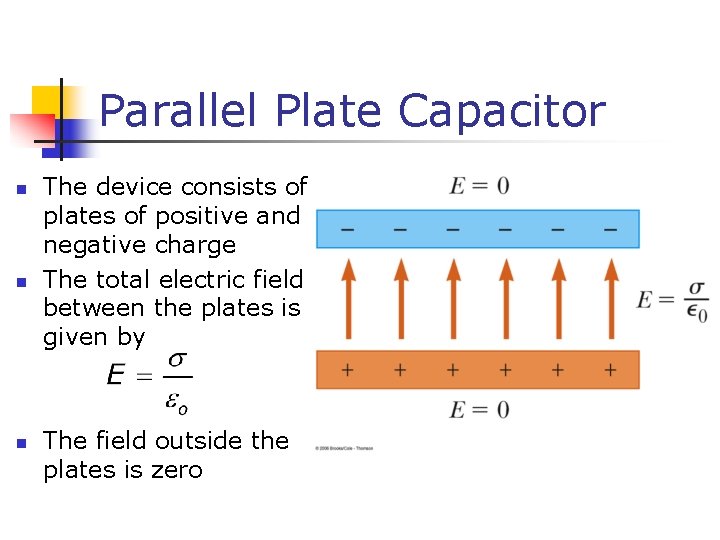
Parallel Plate Capacitor n n n The device consists of plates of positive and negative charge The total electric field between the plates is given by The field outside the plates is zero