Lecture 3 Ch 3 5 System of Linear

Lecture 3 Ch 3. 5 System of Linear Equations Delivered by: Iksan Bukhori iksan. bukhori@president. ac. id Matrices & Vector Spaces 2018

System of Linear Equation � Linear equation is an equation where all variables are in the first order of power with no product, roots, logarithmic, or trigonometric form.

System of Linear Equations • a linear equation in n variables: a 1, a 2, a 3, …, an, b: real number a 1: leading coefficient x 1: leading variable n Notes: (1) Linear equations have no products or roots of variables and no variables involved in trigonometric, exponential, or logarithmic functions. (2) Variables appear only to the first power.

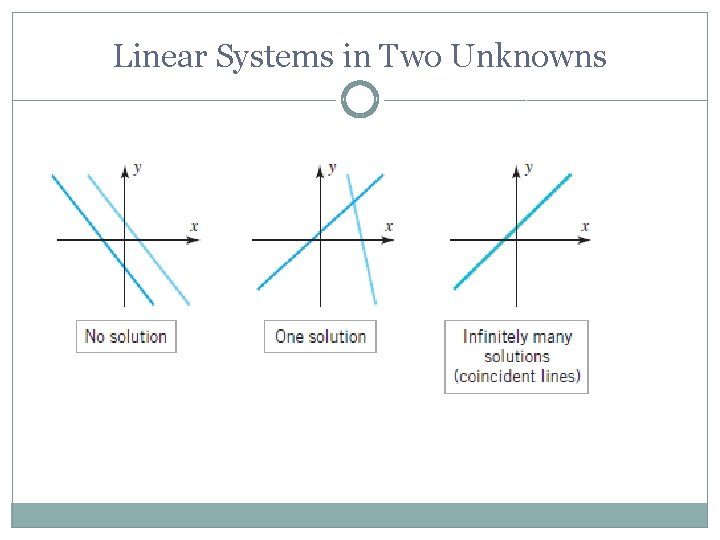
System of Linear Equations • a linear equation in n variables: a 1, a 2, a 3, …, an, b: real number a 1: leading coefficient n Examples: (a) x 1 + 2 x 2 = 5 2 x 1 + 3 x 2 = 8 x 1: leading variable (b) x 1 – x 2 +x 3 = 2 2 x 1 + x 2 - x 3 = 4 (c) x 1 + x 2 = 2 x 1 - x 2 = 1 x 1 =4 If the system has no solution, we say that the system is inconsistent. If the system has at least one solution, we say that it is consistent.

Linear Systems in Two Unknowns

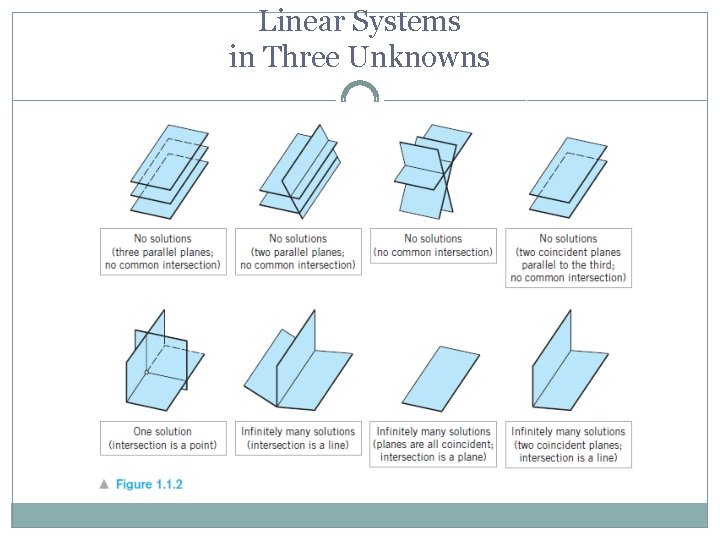
Linear Systems in Three Unknowns

System of Linear Equations • a system of m linear equations in n variables: n Consistent: A system of linear equations has at least one solution. n Inconsistent: A system of linear equations has no solution.

Practice! Find solution for this equation: What method will you use? • Elimination - Substitution • Elementary Row Operation

More Practice! � Elementary Row Operations 1. Interchange two What method will you use? • Elimination - Substitution • Elementary Row Operation rows. 2. Multiply a row by a nonzero real number. 3. Replace a row by its sum with a multiple of another row.

More Practice! � Elementary Row Operations 1. Interchange two What method will you use? • Elimination - Substitution • Elementary Row Operation • Gauss Elimination rows. 2. Multiply a row by a nonzero real number. 3. Replace a row by its sum with a multiple of another row.

Row Echelon Form and Reduced Row Echelon Form (Gauss Jordan Elimination) Row Echelon Form Reduced row Echelon Form � All nonzero rows (rows � The matrix should be in row with at least on nonzero element) are above any rows of all zeroes (all zero rows), if any belong at the bottom of the matrix � The leading coefficient (the first nonzero number from the left, also called the pivot) of a nonzero row is always strictly farther to the right of the leading coefficient of the row above it (some texts add the condition that the leading coefficient must be 1) echelon form � Every leading coefficient is 1 and is the only nonzero entry in its column

Row Echelon Form and Reduced Row Echelon Form (Gauss Jordan Elimination)

Row Echelon Form and Reduced Row Echelon Form (Gauss Jordan Elimination) �If we use only the first five steps, the above procedure produces a row-echelon form and is called Gaussian elimination. �Carrying the procedure through to the sixth step and producing a matrix in reduced row-echelon form is called Gauss–Jordan elimination.

Answer review (1)

Answer review (2)

Answer review (3)

Elimination methods Soal:

If we use only the first five steps, the above procedure produces a rowechelon form and is called Gaussian elimination. Carrying the procedure through to the sixth step and producing a matrix in reduced row-echelon form is called Gauss–Jordan elimination.

Homework 1: System of Linear Equation �

THANK YOU