Lecture 3 Attenuation Dispersion EMT 494 Optical Communication

Lecture 3 Attenuation & Dispersion EMT 494 Optical Communication By Halim

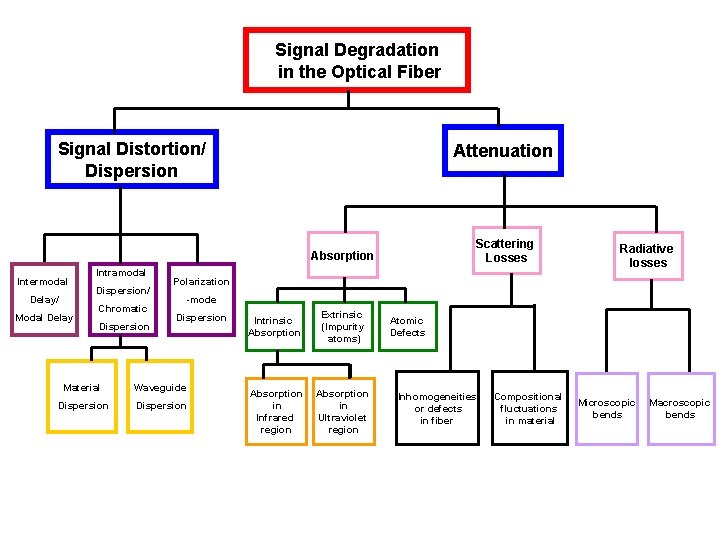
Signal Degradation in the Optical Fiber Signal Attenuation-signal loss It determines the maximum unamplified or repeaterless distance between transmitter and receiver. Signal Distortion-signal dispersion • Causes optical pulses broaden. • Overlapping with neighboring pulses, creating errors in the receiver output. • It limits the information carrying capacity of a fiber.

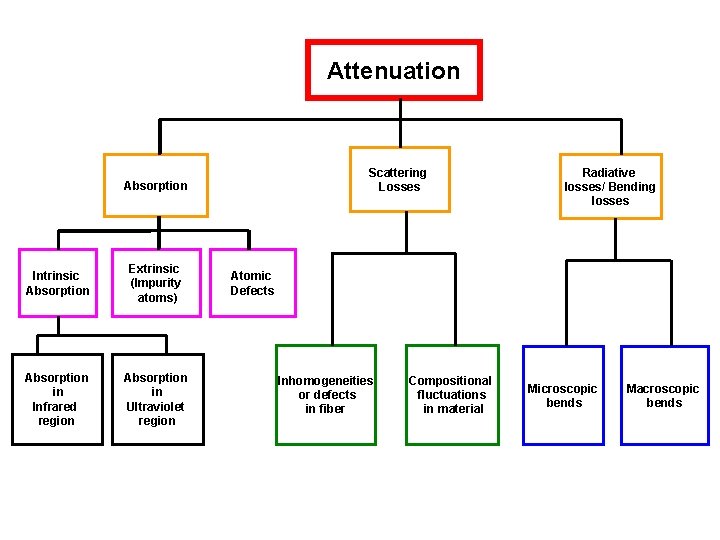
Attenuation The Basic attenuation mechanisms in a fiber: 1. Absorption: It is related to the fiber material. 2. Scattering: It is associated both with the fiber material and with the structural imperfections in the optical waveguide. 3. Radiative losses/ Bending losses: It originates from perturbation (both microscopic and macroscopic) of the fiber geometry.

Example: Absorption by Atmospheric

Example: Scattering of light by Atmospheric The colours of the sky are caused by the scattering of light

Attenuation Units If P(0) is the optical power in a fiber at the origin (at z=0), then the power P(z) at a distance z P(z) =P (0) e -αpz αp = (1/z) ln [P(0) / P(z)] Fiber attenuation coefficient Attenuation coefficient in units of decibels per kilometer, denoted by d. B/ Km, then α(d. B/km) = (10/z) ln [P(0) / P(z)]=4. 343 x αp (km-1)

Q: Fiber has an attenuation of 0. 4 d. B/km at a wavelength of 1310 nm. Then after it travels 50 km, what is the optical power loss in the fiber ? Q: Optical powers are commonly expressed in units of d. Bm, which is the decibel power level referred to 1 m. W. Consider a 30 km long optical fiber that has an attenuation of 0. 4 d. B/km at 1310 nm. Find the optical output power Pout, if Pin is 200 μW

Absorption is caused by three different mechanisms: 1 - Impurities in fiber material: from transition metal ions & particularly from OH ions with absorption peaks at wavelengths 2700 nm, 400 nm, 950 nm & 725 nm. 2 - Intrinsic absorption : electronic absorption band (UV region) & atomic bond vibration band (IR region) in basic Si. O 2. 3 - Radiation defects-damages internal structure of materials

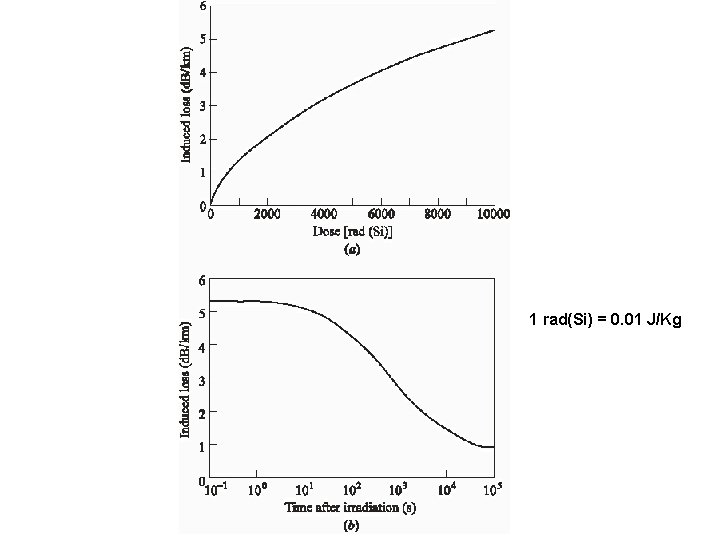
Absorption 1. Absorption by atomic defects Atomic defects are imperfections in the atomic structure of the fiber material. Examples: • Missing molecules • High density clusters of atom groups • Oxygen defects in the glass structure. • Absorption losses arising from these defects are negligible compared with intrinsic( energy band) and impurity absorption. • Can be significant if the fiber is exposed to ionization radiations.

1 rad(Si) = 0. 01 J/Kg

Absorption 2. Extrinsic absorption by impurity atoms The dominant absorption factor in silica fibers is the presence of small quantities of impurities in the fiber material. • These impurities include • OH- (water) ions dissolved in the glass. • Transition metal ions, such as iron, copper, chromium and vanadium Origin : OH ion impurities in a fiber preform results mainly from the oxyhydrogen flame used in the hydrolysis reaction of the Si. Cl 4, Ge. Cl 4 and POCl 3 starting materials.

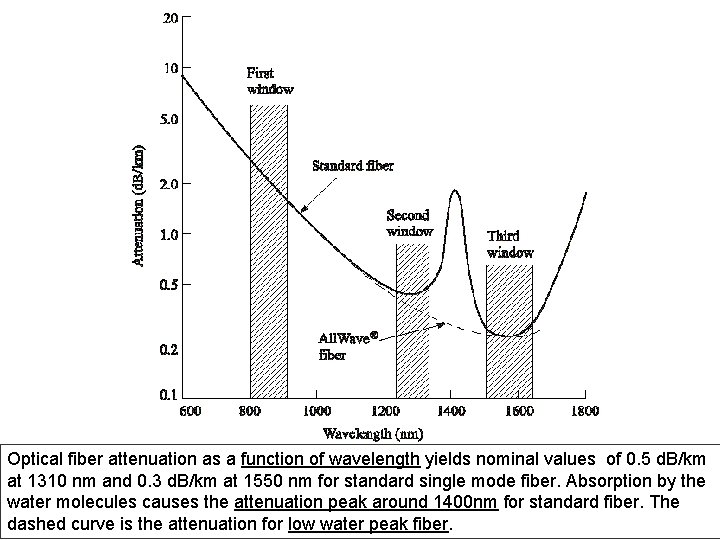
Optical fiber attenuation as a function of wavelength yields nominal values of 0. 5 d. B/km at 1310 nm and 0. 3 d. B/km at 1550 nm for standard single mode fiber. Absorption by the water molecules causes the attenuation peak around 1400 nm for standard fiber. The dashed curve is the attenuation for low water peak fiber.

Absorption 3. Intrinsic absorption by the basic constituent atoms Intrinsic absorption is associated with the basic fiber material (e. g pure Si. O 2). Intrinsic absorption results from: 1. Electronic absorption bands in the ultraviolet region 2. Atomic vibration bands in the near infrared region

Absorption 1. Electronic absorption (EA) occurs when a photon interacts with an electron in the valance band excites it to a higher energy level. The electronic absorption is associated with the band gap of the material. The UV edge of EA follow the empirical formula Ultraviolet absorption decays exponentially with increasing wavelength and is small compared with scattering loss in the near infrared region. UV loss in d. B/km at any as a function of mole fraction x of Ge. O 2 is

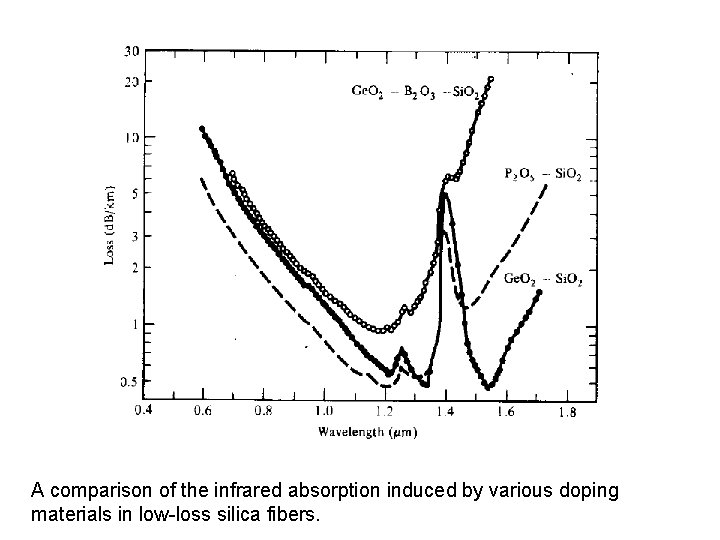
2. The inherent infrared absorption is associated with the vibration frequency of chemical bond between the atoms of which the fiber is composed. An interaction between the vibrating bond and the electromagnetic field of the optical signal results in a transfer of energy from the field to the bond and thereby giving rise to absorption. This absorption is quite strong because of many bonds present in the fiber. Example: Ge. O 2 -Si. O 2.

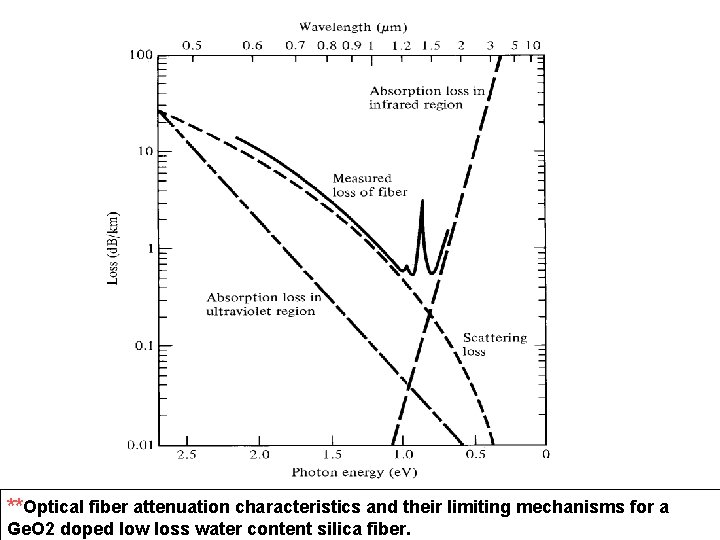
**Optical fiber attenuation characteristics and their limiting mechanisms for a Ge. O 2 doped low loss water content silica fiber.

A comparison of the infrared absorption induced by various doping materials in low-loss silica fibers.

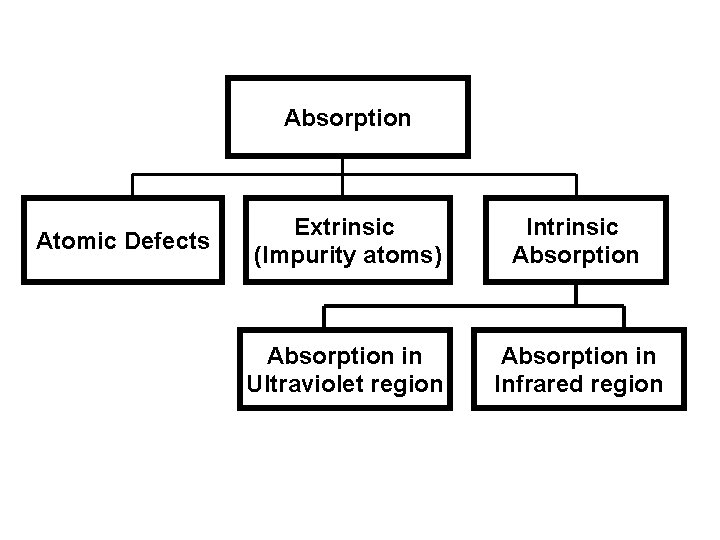
Absorption Atomic Defects Extrinsic (Impurity atoms) Intrinsic Absorption in Ultraviolet region Absorption in Infrared region

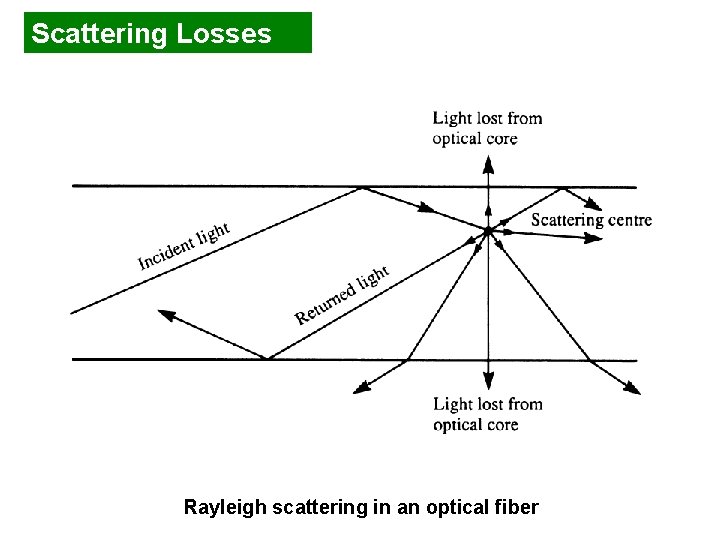
Scattering Losses Scattering losses in glass arise from microscopic variation in the material density from: 1. Compositional fluctuations-density of components 2. Inhomogeneities or defects occurring during fiber manufacturestructural defects These two effects give rise to refractive index variation, occurring within the glass over distances that are small compared with the wavelength. These index variation case Rayleigh-type scattering of the light and inversely proportional to wavelength. It decreases dramatically with increasing wavelength

Scattering Losses Rayleigh scattering in an optical fiber

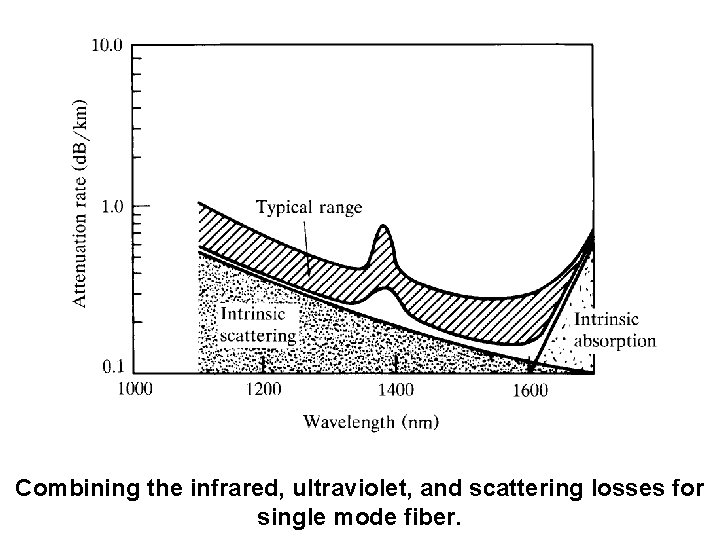
Combining the infrared, ultraviolet, and scattering losses for single mode fiber.

Scattering Losses Compositional fluctuations Inhomogeneities or defects in material in fiber

Radiative losses / Bending Losses Radiative losses occur whenever an optical fiber undergoes a bend of finite radius of curvature. Fiber can be subject to two types of bends: 1. Macroscopic bends 2. Microscopic bends Macrobending: Light lost from the optical core due to macroscopic effects such as tight bends being induced in the fiber itself. Microbending. Light lost from the optical core due to microscopic effects resulting from deformation and damage to the core cladding interface.

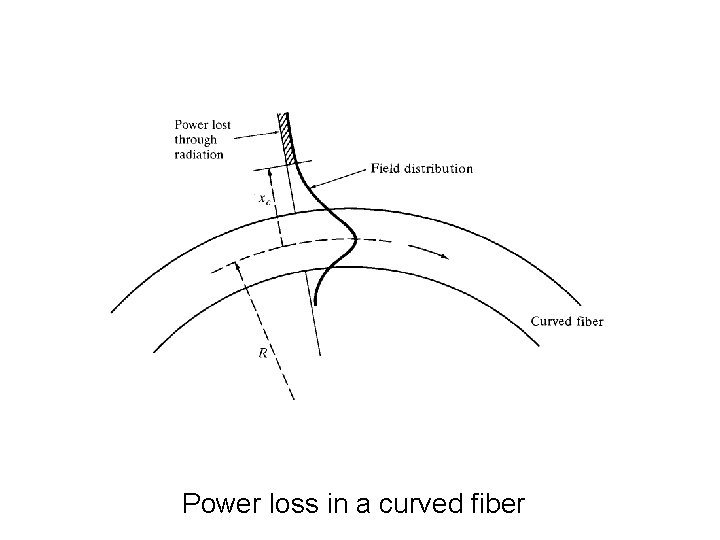
Radiative losses / Bending Losses • For the slight bends losses are unobservable • By decreasing radius of curvature we will come to the critical value after which these losses increase drastically, shown as xc in the fig. • As we know that the electric/magnetic field have a tail in the cladding region so by bending the cable we come to the extent where cladding field should move faster to keep up with the core field. • As this is not possible so the energy in that region radiates away • Radiation losses depend on the value of xc and radius of curvature R • As the lower order modes remain close to the core axis and the higher modes are closer to the cladding so the higher modes will radiate out of the fiber first.

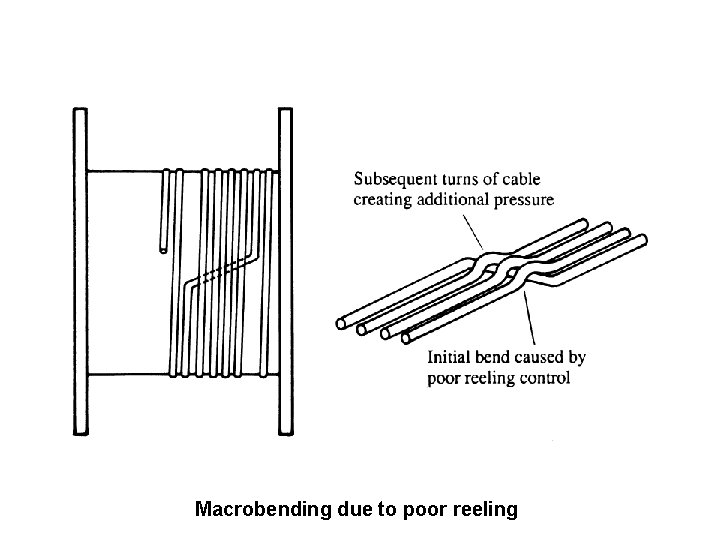
Radiative losses / Bending Losses Macrobending losses are normally produced by poor handling of fiber. Poor reeling and mishandling during installation can create severe bending of the fiber resulting in small but important localized losses

Power loss in a curved fiber

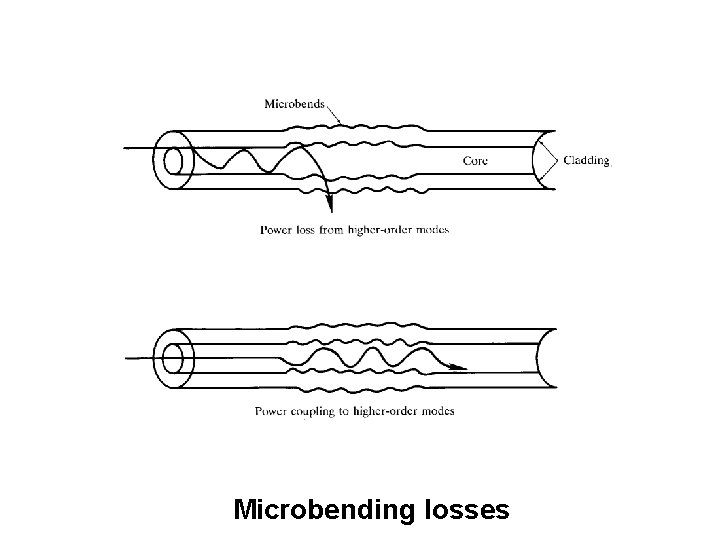
Radiative losses / Bending Losses Microbending losses: It is the radiation loss in optical waveguide results from mode coupling by random microbends. Fiber curvature causes repetitive coupling of energy between the guided modes and the leaky or nonguided modes in the fiber. Microbending is a much more critical feature and can be a major cause of cabling attenuation. These stresses are very difficult to define, however, they can be caused by: • nonuniformities in the manufacturing of the fiber • nonuniform lateral pressures during cabling • Low temperatures • High pressures

Microbending losses

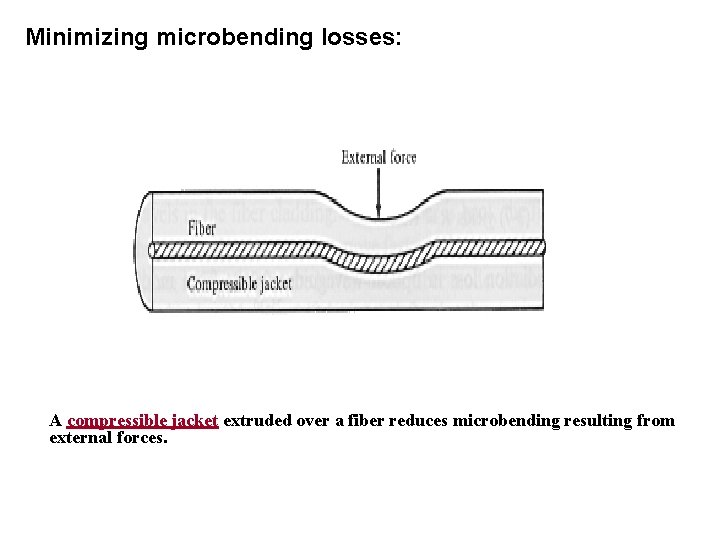
Minimizing microbending losses: A compressible jacket extruded over a fiber reduces microbending resulting from external forces.

Macrobending due to poor reeling

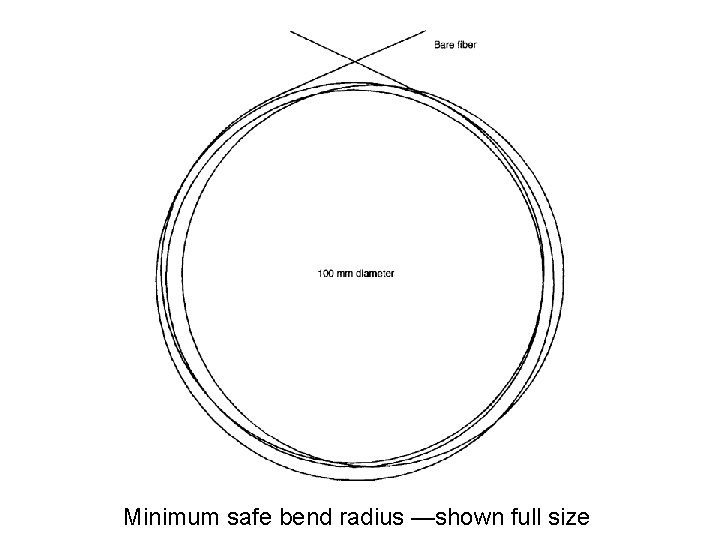
Minimum safe bend radius —shown full size

Bends are shown full size — and may have caused damage to the fiber

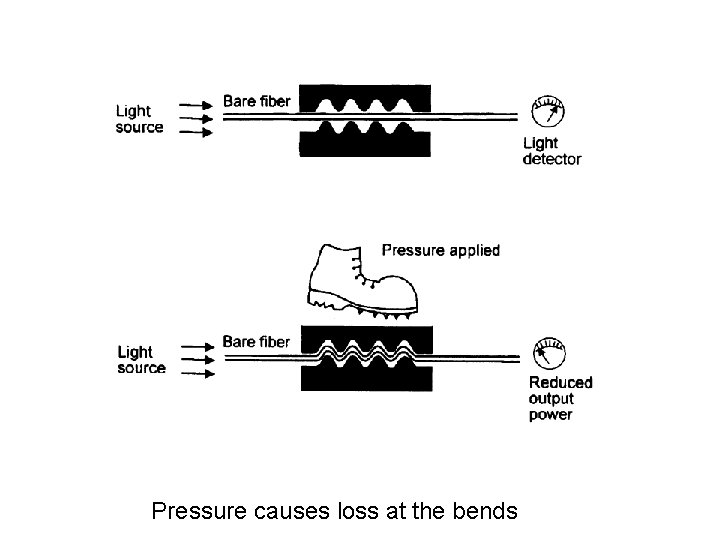
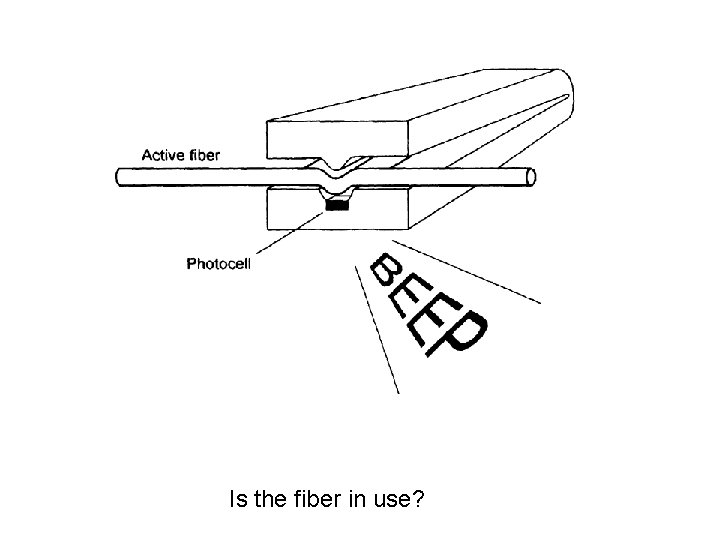
Radiative losses / Bending Losses Making use of bending losses There are many uses of bending losses which are based on either the increase in the attenuation or on making use of the light which escapes from the optic fiber. A fiber optic pressure sensor This makes use of the increased attenuation experienced by the fiber as it bends. Active fiber detector This uses the escaping light.

Pressure causes loss at the bends

Is the fiber in use?

Radiative losses/ Bending losses Macroscopic bends Microscopic bends

Attenuation Scattering Losses Absorption Intrinsic Absorption Extrinsic (Impurity atoms) Absorption in Infrared region Absorption in Ultraviolet region Radiative losses/ Bending losses Atomic Defects Inhomogeneities or defects in fiber Compositional fluctuations in material Microscopic bends Macroscopic bends

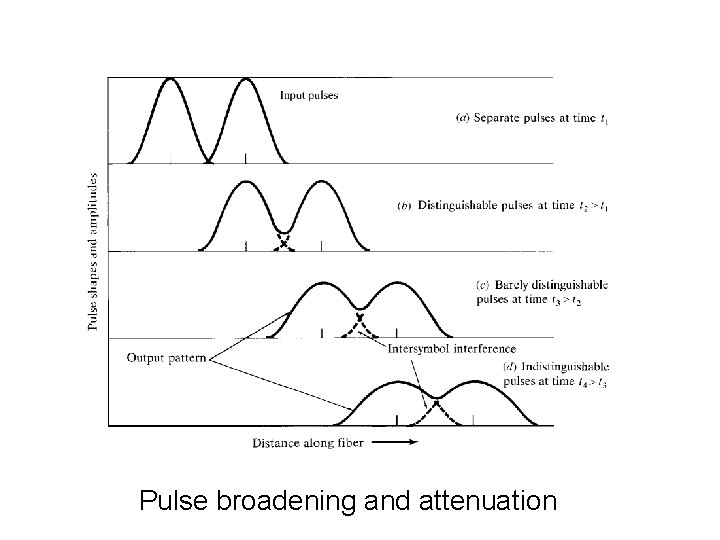
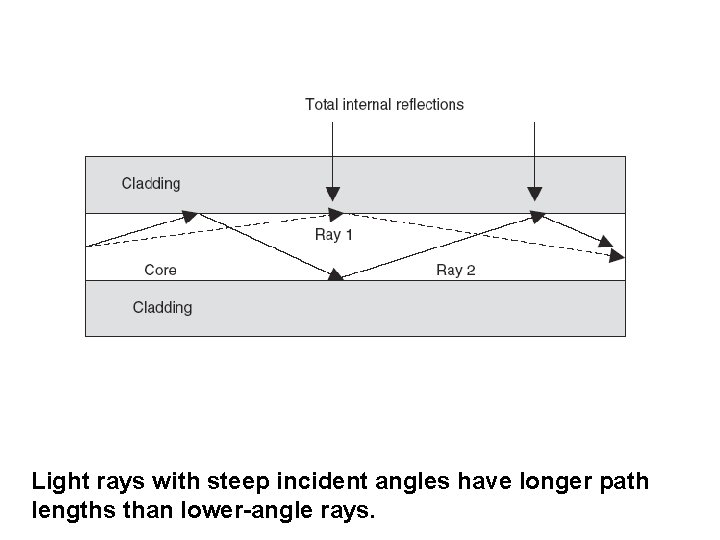
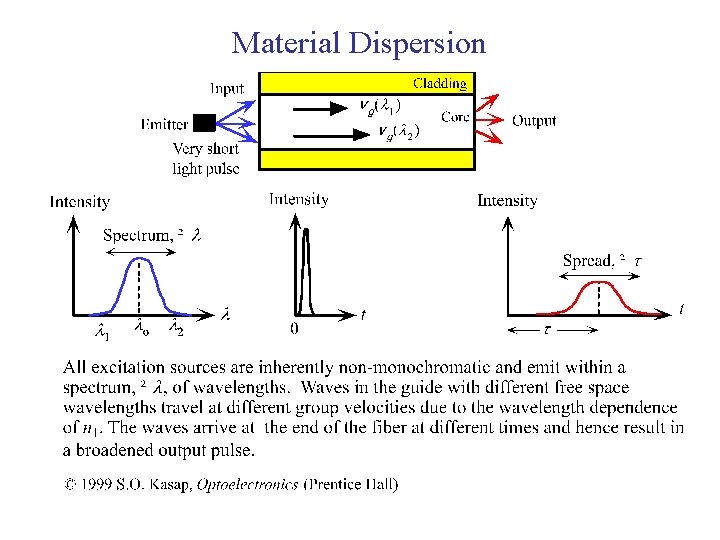
Signal Distortion/Dispersion in Fibers Optical signal weakens from attenuation mechanisms and broadens due to distortion effects. Eventually these two factors will cause neighboring pulses to overlap. After a certain amount of overlap occurs, the receiver can no longer distinguish the individual adjacent pulses and error arise when interpreting the received signal.

Pulse broadening and attenuation

Dispersion 2 The basic need is to match the output waveform to the input waveform as closely as possible. 2 Attenuation only reduces the amplitude of the output waveform which does not alter the shape of the signal. 2 Dispersion distorts both pulse and analog modulation signals.

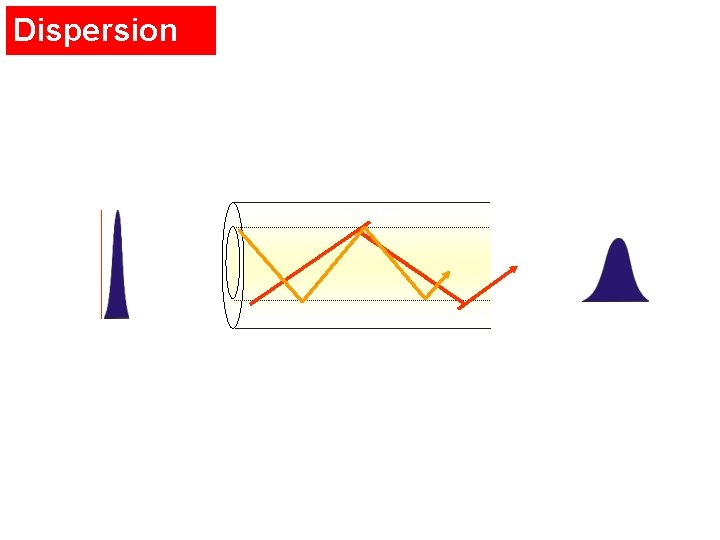
Dispersion results when some components of the input signal spend more time traversing the fiber than other components. 2 In a pulse modulated system, this causes the received pulse to be spread out over a longer period. 2 It is noted that actually no power is lost to dispersion, the spreading effect reduces the peak power.

Dispersion

Dispersion 2 Pulse dispersion is usually specified in terms of “Nanoseconds-per-kilometer”. 2 The difference in width of an input pulse with the width of the same pulse at the output, measured in time, is the dispersion characteristic for that piece of fiber.

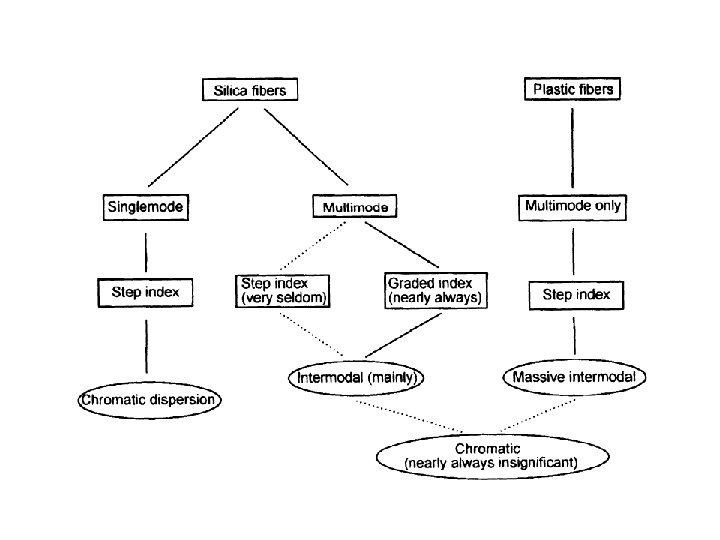
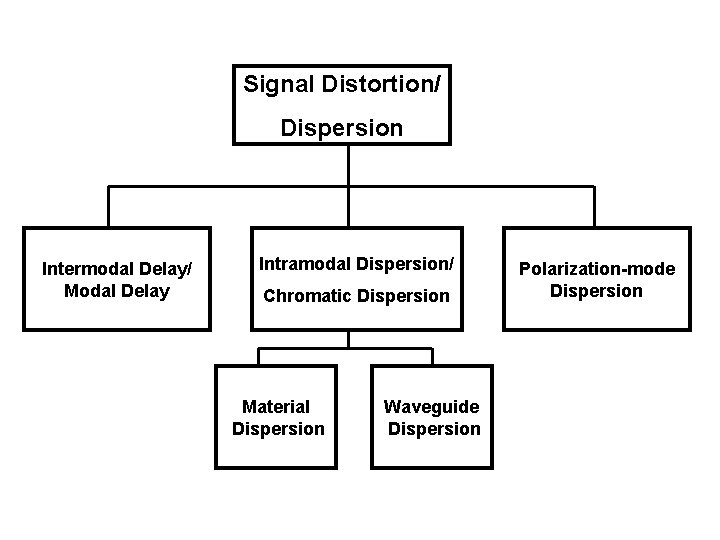
Dispersion of optical energy within an optical fiber falls into following categories: Ø Intermodal Delay or Modal Delay) Ø Intramodal Dispertion or Chromatic Dispersion ØMaterial Dispertion ØWaveguide Dispertion Ø Polarization –Mode Dispersion

Dispersion Intermodal delay/ modal delay Intermodal distortion or modal delay appears only in multimode fibers. This signal distortion mechanism is a result of each mode having a different value of the group velocity at a single frequency. The amount of spreading that occurs in a fiber is a function of the number of modes propagated by the fiber and length of the fiber Group Velocity: It is the speed at which energy in a particular mode travels along the fiber.

Intermodal delay/ modal delay The maximum pulse broadening arising from the modal delay is the difference between the travel time Tmax of the longest ray and the travel time Tmin of the shortest ray. This broadening is simply obtained from ray tracing for a fiber of length L: ∆T= Tmax – Tmin = n 1/c ( L/sinøc –L) = (Ln 12/cn 2)∆ ∆T= Tmax – Tmin = (Ln 12/cn 2)∆

Intermodal delay/ modal delay Fiber Capacity: Fiber capacity is specified in terms of the bit rate-distance product BL. (Bit rate times the possible transmission distance L) For neighboring signal pulses to remain distinguishable at the receiver, the pulse spread should be less than 1/B. Or Pulse spread should be less than the width of a bit period. ∆T < 1 /B General requirement ∆T ≤ 0. 1 /B For high performance link Bit rate distance product BL < n 2 c/ n 12 ∆

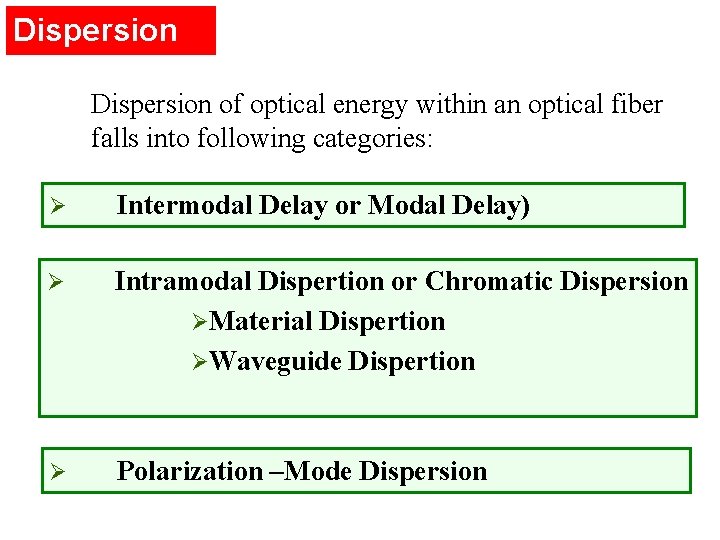
Light rays with steep incident angles have longer path lengths than lower-angle rays.

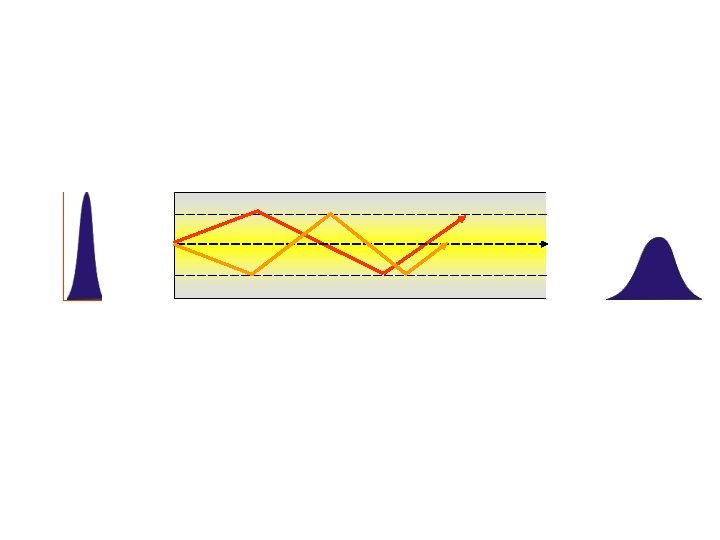
How to minimize the effect of modal dispersion? Answer is 1. Graded index fiber 2. Single mode fiber How to get one mode and solve the problem V = 2πa / λ x (n 12 – n 22)1/2 = 2πa / λ x (NA)

How to get one mode and solve the problem we could decrease the number of modes by increasing the wavelength of the light. Changing from the 850 nm window to the 1550 nm window will only reduce the number of modes by a factor of 3 or 4. Change in the numerical aperture can help but it only makes a marginal improvement. We are left with the core diameter. The smaller the core, the fewer the modes. When the core is reduced sufficiently the number of modes can be reduced to just one.

Step Index Multi-mode Graded Index Multi-mode

Q: Consider a 1 Km long multimode fiber in which 1. 480 and ∆ = 0. 10 , so that n 2= 1. 465. Then find ∆T= ? Where: L = 1 Km n 1 = 1. 480 n 2= 1. 465 ∆ = 0. 10 ∆T = (Ln 12/cn 2)∆ n 1=

How to characterize dispersion? • Group delay per unit length can be defined as: [3 -15] • If the spectral width of the optical source is not too wide, then the delay difference per unit wavelength along the propagation path is approximately For spectral components which are apart, symmetrical around center wavelength, the total delay difference over a distance L is: [3 -16]

• is called GVD parameter, and shows how much a light pulse broadens as it travels along an optical fiber. The more common parameter is called Dispersion, and can be defined as the delay difference per unit length per unit wavelength as follows: [3 -17] • In the case of optical pulse, if the spectral width of the optical source is characterized by its rms value of the Gaussian pulse , the pulse spreading over the length of L, can be well approximated by: [3 -18] • D has a typical unit of [ps/(nm. km)].

Dispersion Intramodal Dispersion or Chromatic Dispersion This takes place within a single mode. Intramodal dispersion depends on the wavelength, its effect on signal distortion increases with the spectral width of the light source. Spectral width is approximately 4 to 9 percent of a central wavelength. Two main causes of intramodal dispersion are as: 1. Material Dispersion 2. Waveguide Dispersion

Material Dispersion

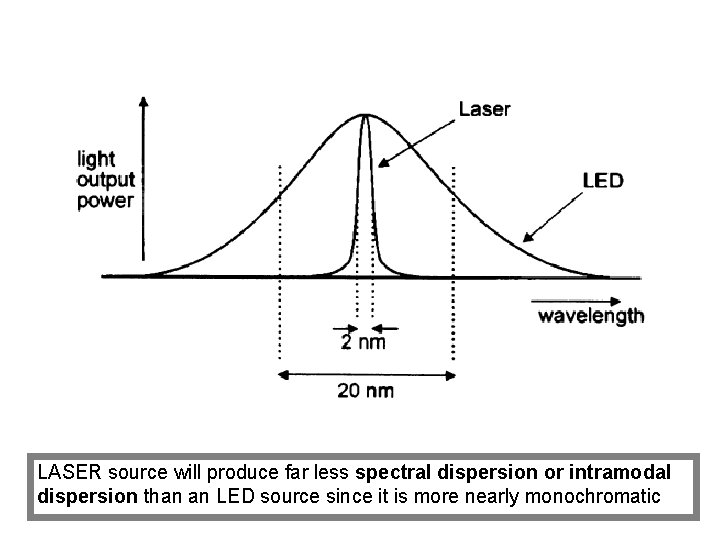
Intramodal Dispersion or Chromatic Dispersion Material Dispersion: This refractive index property causes a wavelength dependence of the group velocity of a given mode; that is, Pulse spreading occurs even when different wavelength follow the same path. Material dispersion can be reduced: • Either by choosing sources with narrower spectral output widths OR • By operating at longer wavelengths.

LASER source will produce far less spectral dispersion or intramodal dispersion than an LED source since it is more nearly monochromatic

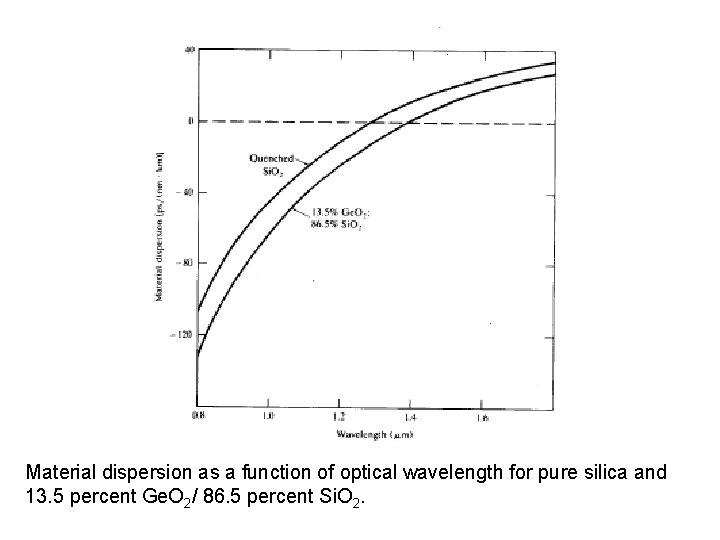
Material Dispersion • The refractive index of the material varies as a function of wavelength, • Material-induced dispersion for a plane wave propagation in homogeneous medium of refractive index n: [3 -19] • The pulse spread due to material dispersion is therefore: [3 -20] is material dispersion

Material dispersion as a function of optical wavelength for pure silica and 13. 5 percent Ge. O 2/ 86. 5 percent Si. O 2.

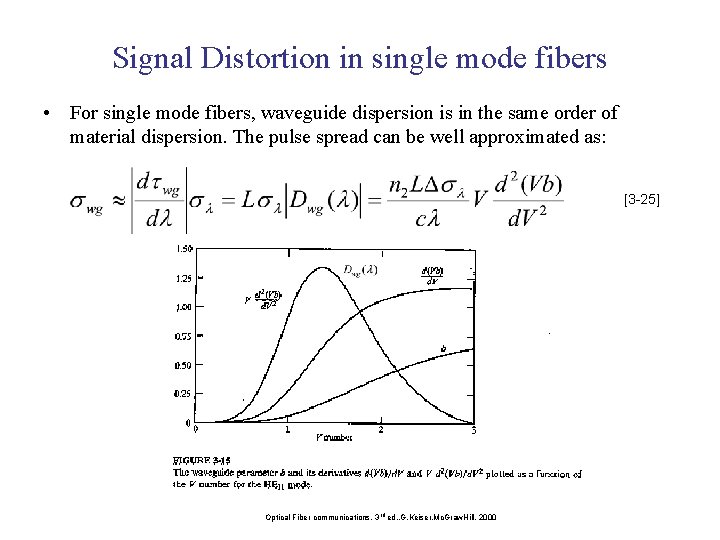
Intramodal Dispersion or Chromatic Dispersion Waveguide Dispersion: It causes pulse spreading because only part of the optical power propagation along a fiber is confined to core. Dispersion arises because the fraction of light power propagating in the cladding travels faster than the light confined to core. Single mode fiber confines only 80 percent of the power in the core for V values around 2. The amount of waveguide dispersion depends on the fiber design.

Waveguide Dispersion • Waveguide dispersion is due to the dependency of the group velocity of the fundamental mode as well as other modes on the V number, (see Fig 2 -18 of the textbook). In order to calculate waveguide dispersion, we consider that n is not dependent on wavelength. Defining the normalized propagation constant b as: [3 -29] • solving for propagation constant: [3 -31] • Using V number: [3 -33]

Waveguide Dispersion • Delay time due to waveguide dispersion can then be expressed as: [3 -34] Optical Fiber communications, 3 rd ed. , G. Keiser, Mc. Graw. Hill, 2000

Signal Distortion in single mode fibers • For single mode fibers, waveguide dispersion is in the same order of material dispersion. The pulse spread can be well approximated as: [3 -25] Optical Fiber communications, 3 rd ed. , G. Keiser, Mc. Graw. Hill, 2000

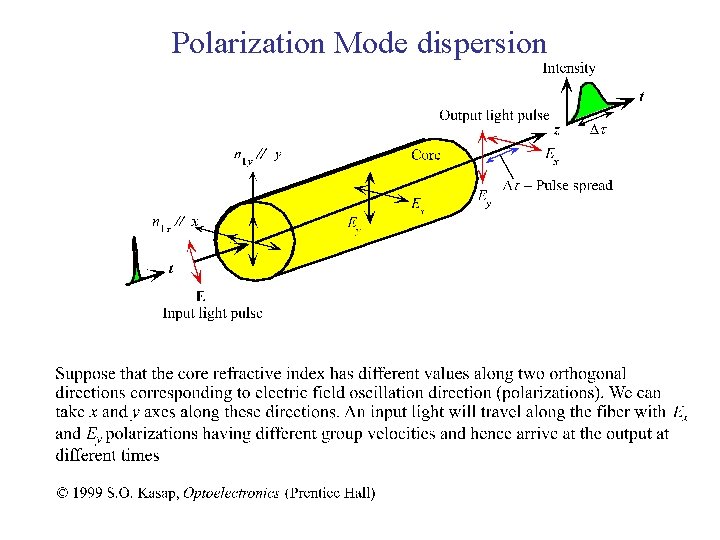
Polarization Mode dispersion

Polarization Mode dispersion • The effects of fiber-birefringence on the polarization states of an optical are another source of pulse broadening. Polarization mode dispersion (PMD) is due to slightly different velocity for each polarization mode because of the lack of perfectly symmetric & anisotropicity of the fiber. If the group velocities of two orthogonal polarization modes are then the differential time delay between these two polarization over a distance L is [3 -26] • The rms value of the differential group delay can be approximated as: [3 -27]

Chromatic & Total Dispersion • Chromatic dispersion includes the material & waveguide dispersions. [3 -28] • Total dispersion is the sum of chromatic , polarization dispersion and other dispersion types and the total rms pulse spreading can be approximately written as: [3 -29]

Chromatic & Total Dispersion • Chromatic dispersion includes the material & waveguide dispersions. [3 -28] • Total dispersion is the sum of chromatic , polarization dispersion and other dispersion types and the total rms pulse spreading can be approximately written as: [3 -29]

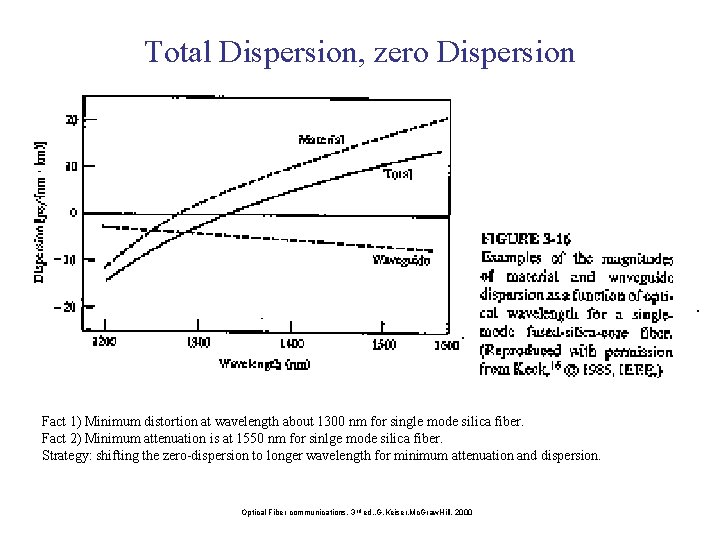
Total Dispersion, zero Dispersion Fact 1) Minimum distortion at wavelength about 1300 nm for single mode silica fiber. Fact 2) Minimum attenuation is at 1550 nm for sinlge mode silica fiber. Strategy: shifting the zero-dispersion to longer wavelength for minimum attenuation and dispersion. Optical Fiber communications, 3 rd ed. , G. Keiser, Mc. Graw. Hill, 2000

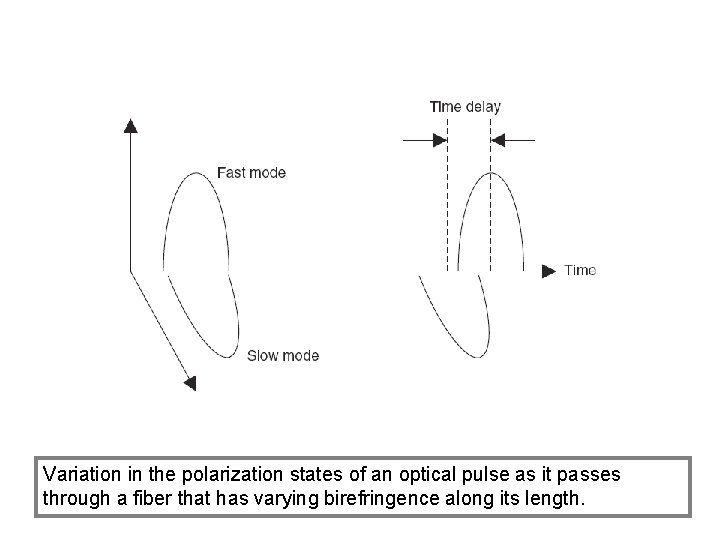
Variation in the polarization states of an optical pulse as it passes through a fiber that has varying birefringence along its length.

Signal Distortion/ Dispersion Intermodal Delay/ Modal Delay Intramodal Dispersion/ Chromatic Dispersion Material Dispersion Waveguide Dispersion Polarization-mode Dispersion

Signal Degradation in the Optical Fiber Signal Distortion/ Dispersion Attenuation Scattering Losses Absorption Intermodal Delay/ Modal Delay Intramodal Dispersion/ Chromatic Dispersion Radiative losses Polarization -mode Dispersion Material Waveguide Dispersion Intrinsic Absorption Extrinsic (Impurity atoms) Absorption in Infrared region Absorption in Ultraviolet region Atomic Defects Inhomogeneities or defects in fiber Compositional fluctuations in material Microscopic bends Macroscopic bends

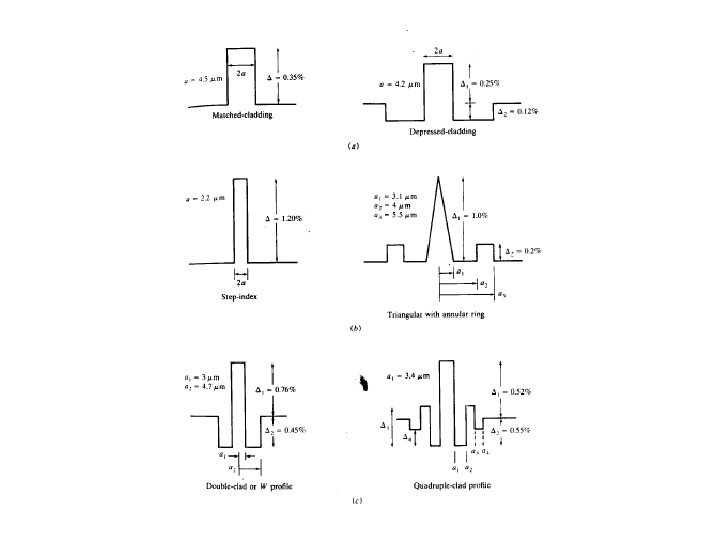
Characteristics of Single Mode Fibers These Characteristics include : 1. Index profile configuration 2. Cutoff wavelength 3. Signal dispersion designations and calculations 4. Mode field diameter 5. Signal loss due to fiber bending.

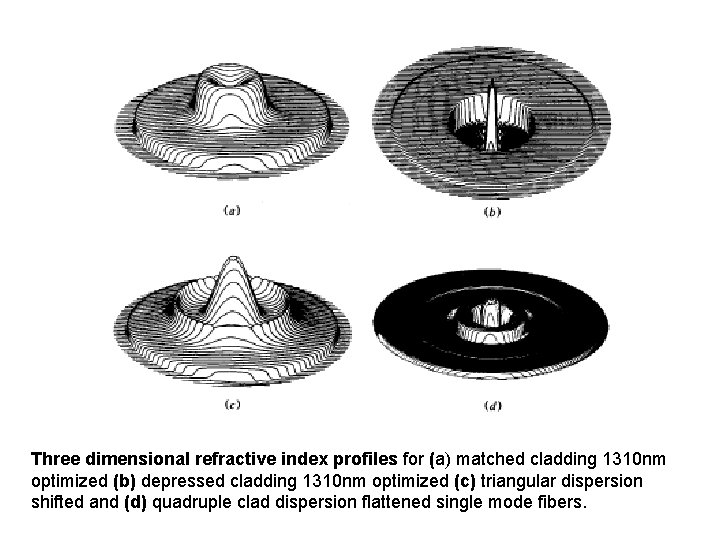
Three dimensional refractive index profiles for (a) matched cladding 1310 nm optimized (b) depressed cladding 1310 nm optimized (c) triangular dispersion shifted and (d) quadruple clad dispersion flattened single mode fibers.

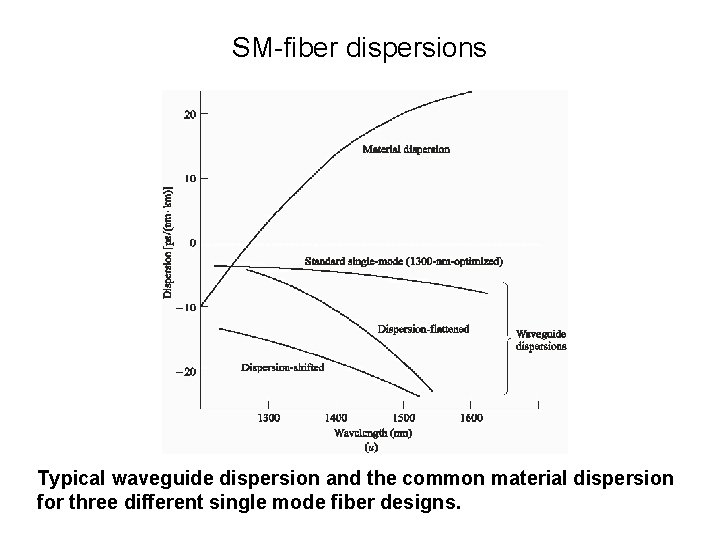
SM-fiber dispersions Typical waveguide dispersion and the common material dispersion for three different single mode fiber designs.

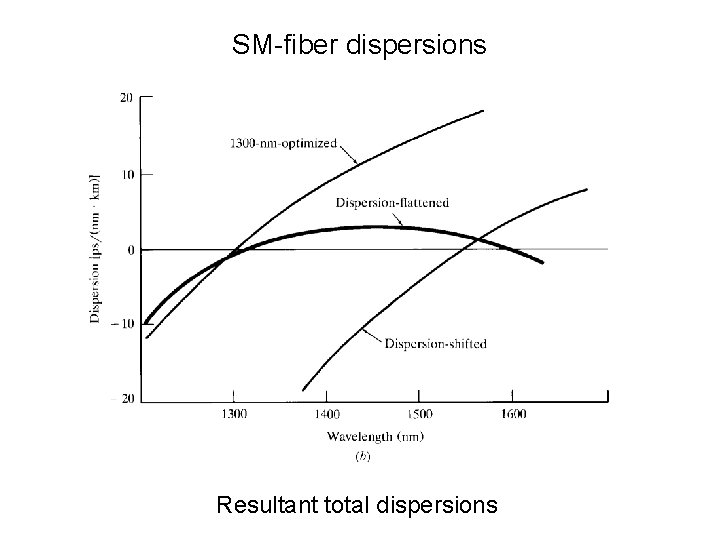
SM-fiber dispersions Resultant total dispersions

Single mode Cut-off wavelength & Dispersion • Fundamental mode is • Dispersion: with V=2. 405 and [3 -30] [3 -31] [3 -32] • For non-dispersion-shifted fibers (1270 nm – 1340 nm) • For dispersion shifted fibers (1500 nm- 1600 nm)

Dispersion for non-dispersion-shifted fibers (1270 nm – 1340 nm) • is relative delay minimum at the zero-dispersion wavelength value of the dispersion slope in. , and is the

Dispersion for dispersion shifted fibers (1500 nm - 1600 nm) [3 -36] [3 -37]

Dispersion Calculation If tmod, t. CD, and t. PMD are the modal, chromatic, and polarization mode dispersion times Then total dispersion t. T can be calculated by the relationship. Note that tmod = 0 for single-mode fibers. Where tcd = |DCD | L ∆λ t. PMD = DPMD (fiber length)1/2

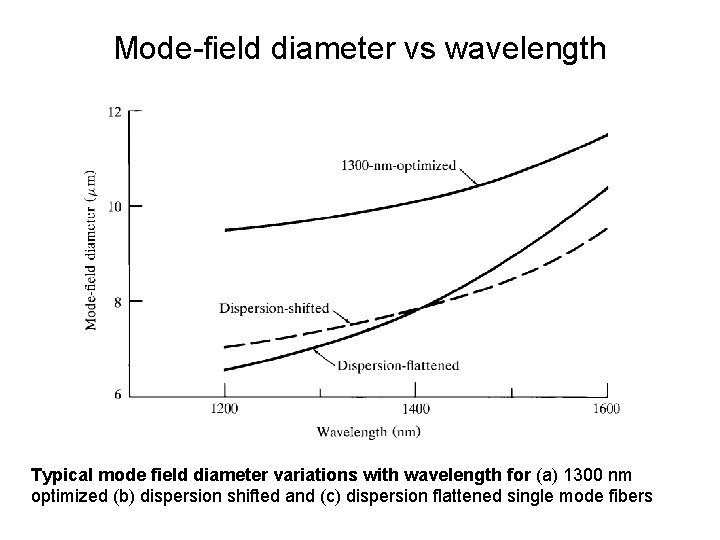
Mode-field diameter vs wavelength Typical mode field diameter variations with wavelength for (a) 1300 nm optimized (b) dispersion shifted and (c) dispersion flattened single mode fibers

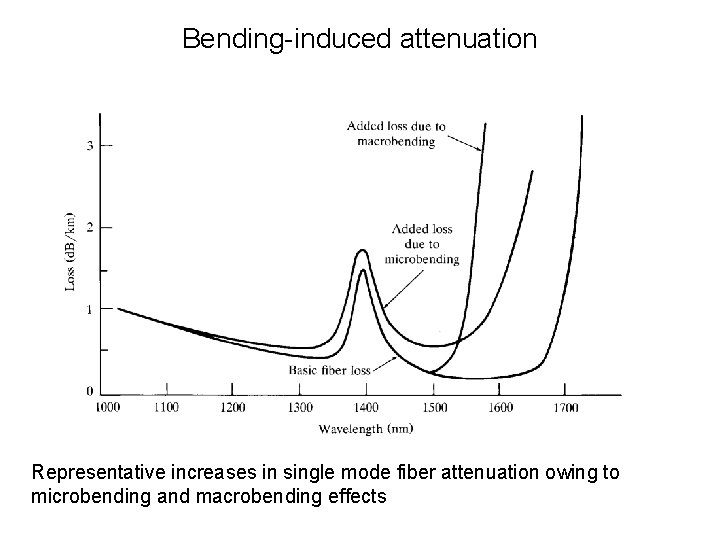
Bending-induced attenuation Representative increases in single mode fiber attenuation owing to microbending and macrobending effects

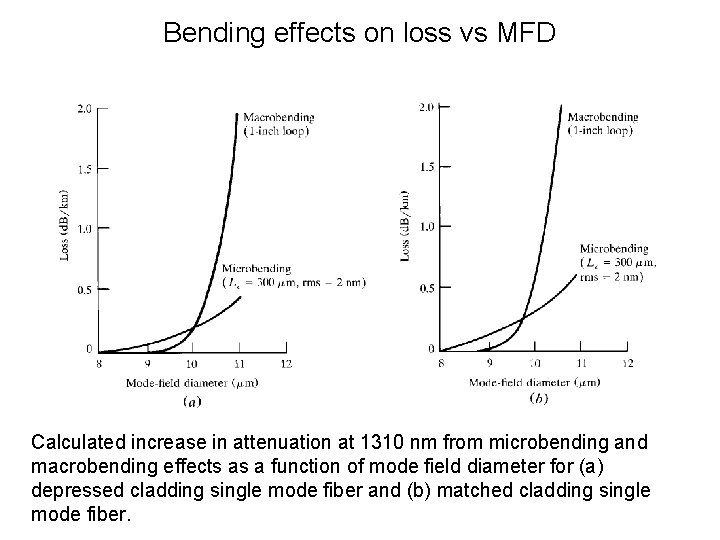
Bending effects on loss vs MFD Calculated increase in attenuation at 1310 nm from microbending and macrobending effects as a function of mode field diameter for (a) depressed cladding single mode fiber and (b) matched cladding single mode fiber.

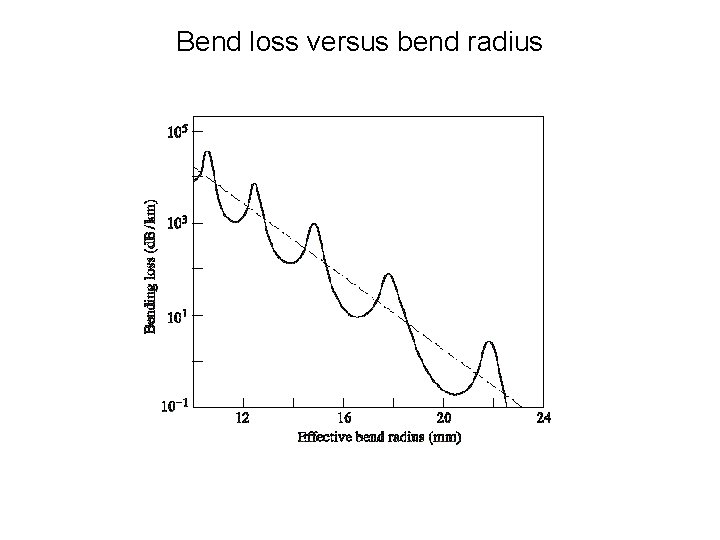
Bend loss versus bend radius

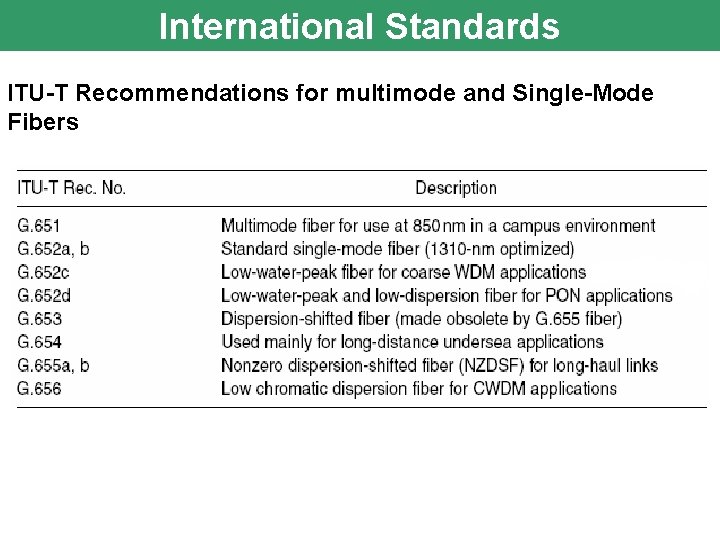
International Standards ITU-T Recommendations for multimode and Single-Mode Fibers

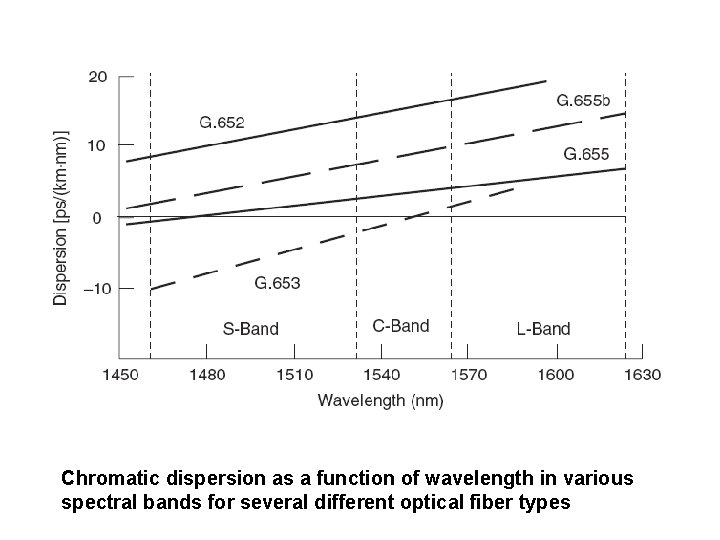
Chromatic dispersion as a function of wavelength in various spectral bands for several different optical fiber types

Recommendation G. 651 Core diameters : 1) 50 µm 2) 62. 5 µm cladding diameters: ( For both fibers) 125 -µm Attenuation : Range form 2. 5 d. B/km at 850 nm to less that 0. 6 d. B/km at 1310 nm Light source used: Vertical cavity surface emitting laser (VSSEL) operating at 850 nm Ethernet links running at data rates up to 10 Gb/s over distance up to 550 m can use multimode fibers

Recommendation G. 652 a/b (Standard single mode fiber or 1300 nm optimized fiber) Installed widely in telecommunication networks in the 1990 s. Core diameter: 5 and 8 µm Cladding diameter: 125µm Max PMD: 0. 2 ps/ √km Attenuation : Range form 0. 4 d. B/km at 1310 nm to less that 0. 35 d. B/km at 1550 nm This fiber was optimized to have a zerodispersion value at 1310 nm. With the trend toward operation in the lower-loss 1550 -nm spectral region, the installation of this fiber has decreased dramatically. If network operators want to use installed G. 652 fiber at 1550 nm, complex dispersion compensation techniques are needed,

Recommendation G. 652 c/d (low water peak fiber) It allows operation in the E-band are used widely for fiber to the premises (FTTP) installations. It is created by reducing the water ion concentration in order to eliminate the attenuation spike in the 1360 to 1460 nm E-band. It allow operation over the entire wavelength range from 1260 to 1625 nm Typically a FTTP link transmits three independent bidirectional channels at 1310, 1490 and 1550 nm over the same fiber.

Recommendation G. 653 (Dispersion shifted fiber DSF) It was developed for the use with 1550 nm lasers. Zero dispersion point is shifted to 1550 nm where the fiber attenuation is about half that at 1310 nm. But It presents dispersion related problems in dense wavelength division multiplexing (DWDM) applications in the centre of the C band. Because To prevent undesirable nonlinear effects in DWDM systems the chromatic dispersion values should be positive or negative over the entire operational band. Therefore The use of G. 653 fibers for DWDM should be restricted to either the S band or L band These fibers are seldom deployed anymore

Recommendation ITU-T G. 654 (cutoff wavelength shifted fiber ) Designed for long distance high power transmission. It has zero dispersion wavelength around 1300 nm wavelength. It has very low loss in the 1550 nm band, which is achieved by using pure silica core. It has a high cutoff wavelength of 1500 nm, restricted to operation in the 1500 to 1600 nm region. Typically used only in long distance undersea application.

Recommendation ITU-T G. 655 (Non zero dispersion shifted fiber ) NZDSF was introduced in the mid 1990 s for WDM applications. Principal characteristic: It has a positive nonzero dispersion value over the entire Cband, which is the spectral operating region for eribium doped optical fiber amplifiers. Version G. 655 b was introduced to extend WDM application into the S-band. Version G. 655 c specifies a lower PMD value of 0. 2 ps√km than the 0. 5 ps/√km value of G. 655 a/b

Recommendation ITU-T G. 656 It has a positive chromatic dispersion value ranging from 2 to 14 ps/(nm-km) in the 1460 to 1625 nm wavelength band. Here dispersion slop is significantly lower than in G. 655 fibers Lower dispersion slope: It means that the chromatic dispersion changes slower with the wavelength so that dispersion compensation is simpler or not needed. This allows The use of CWDM without chromatic dispersion compensation and Also means that 40 additional DWDM channels can be implemented in this wavelength band.

Specialty Fibers Designed to Manipulate or control some characteristic of an optical fiber. The light manipulation applications include: 1. Optical signal amplification 2. Optical power coupling 3. Dispersion compensation 4. Wavelength conversions 5. Sensing of physical parameters: 1. Temperature 2. Stress 3. Pressure 4. Vibration 5. Fluid levels

Specialty Fibers Specialty fibers can be of either a multimode or a single mode design. Optical devices that may use such fibers are: 1. Light transmitters 2. Light modulators 3. Optical receivers 4. Wavelength multiplexers 5. Light couplers 6. Splitters 7. Optical amplifiers 8. Optical switches 9. Wavelength add /drop modules 10. Optical attenuators

Example of Specialty Fibers and Their Applications

Generic Parameter Values of an Erbium-Doped Fiber for Use in the C-Band

Core Cladding Cross-sectional geometry of four different polarizationmaintaining fibers

End-face patterns of two possible holey fiber structures.