Lecture 3 3 Boolean operations fundamentals 3 1

Lecture 3 3. Boolean operations –fundamentals 3. 1 Basic logic functions 3. 2 Further logic operations 3. 3 Establishing switching functions 3. 4 Simplification of logic functions 3. 5 Karnaugh-Veitch diagram

3. 1 Basic logic functions • As described in the previous, any computer and equally any PLC operates using the number system to the base 2. • This also applies to the octal (2 powered by 3) and the hexadecimal systems (2 powered by 4). • The individual variable can therefore assume only two values, „ 0" or "1". • Special algorithms have been introduced to be able to link these variables - the so-called boolean algebra. • This can be clearly represented by means of electrical contacts.
Basic logic functions – 2 Negation (NOT function) Situation

Basic logic functions – 3 Negation (NOT function) Description of the function The push button shown represents normally closed contact (NCC). When this is unactuated, lamp H 1 is illuminated, whereas in the actuated state, lamp H 1 goes off. Push button S 1 acts as signal input (I), the lamp H 1 forms the output (O). The actual status can be recorded in a truth table.
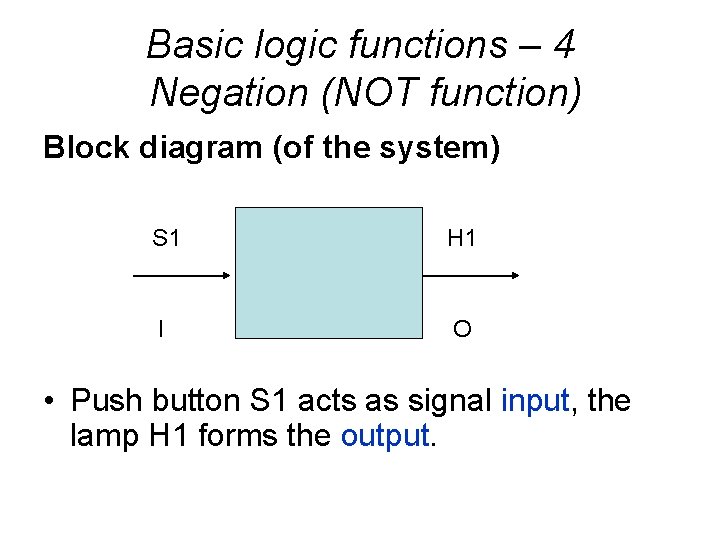
Basic logic functions – 4 Negation (NOT function) Block diagram (of the system) S 1 H 1 I O • Push button S 1 acts as signal input, the lamp H 1 forms the output.
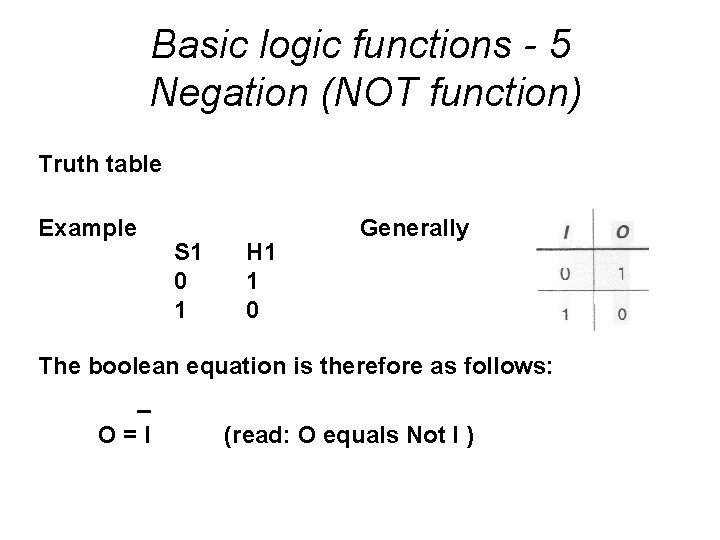
Basic logic functions - 5 Negation (NOT function) Truth table Example S 1 0 1 H 1 1 0 Generally The boolean equation is therefore as follows: _ O=I (read: O equals Not I )
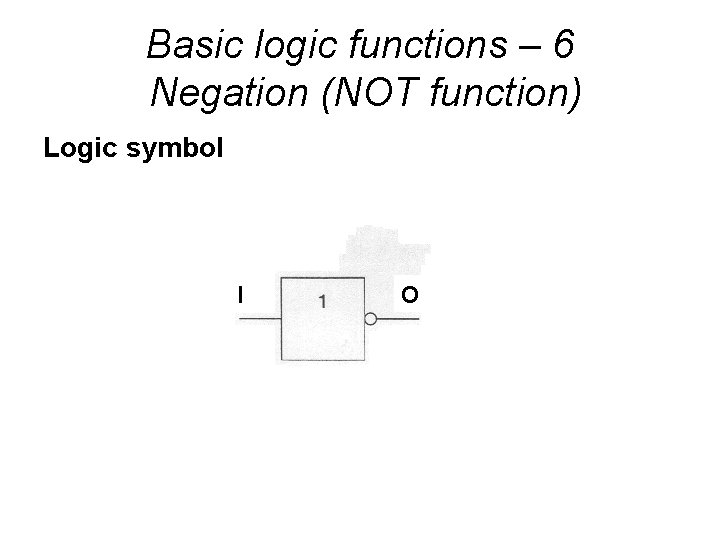
Basic logic functions – 6 Negation (NOT function) Logic symbol I O

Basic logic functions - 7 Negation (NOT function) • If two negations are switched in succession, then these cancel one another I 1 O 1=neg. I 1=I 2 O 2=neg. I 1=I 1

Basic logic functions - 8 Conjunction (AND function) Situation See the overview ( snap No. 67)

Basic logic functions - 9 Conjunction (AND function) Description of the function If two normally open contacts (NOC) S 1 and S 2 are switched in series, the actuated lamp H 1 is illuminated only if both push buttons are actuated.
Basic logic functions - 10 Conjunction (AND function) Block diagram (of the system) S 1 H 1 S 2

Basic logic functions – 11 Conjunction (AND function) Truth table example S 1 S 2 H 1 0 0 1 1 1 generally I 1 I 2 O 0 0 1 1 1
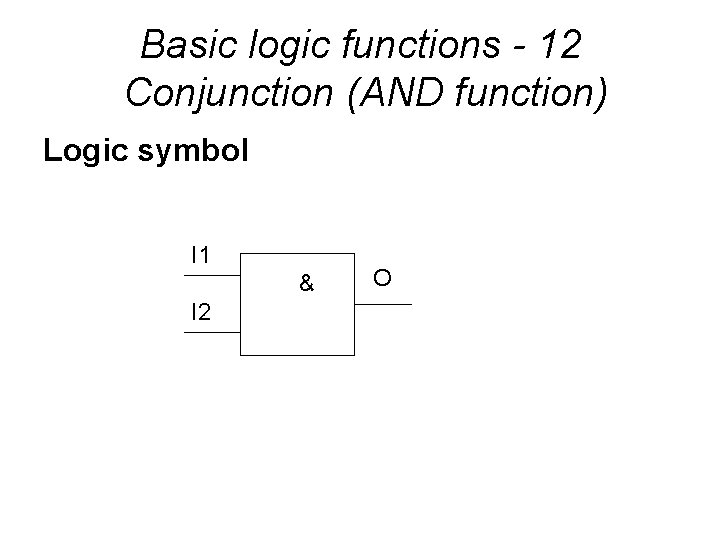
Basic logic functions - 12 Conjunction (AND function) Logic symbol I 1 & I 2 O

Basic logic functions - 13 Conjunction (AND function) Important equations a. 0=0 a. 1=a a. Na =0 a. a=a

Basic logic functions - 14 Disjunction (OR function) Situation See the overview ( snap No. 67)

Basic logic functions - 15 Disjunction (OR function) Description of the function If the 2 normally open contacts (NOC) S 1 and S 2 are switched in parallel, then the lamp H 1 is illuminated whenever at least one push button is pressed.
Basic logic functions - 16 Disjunction (OR function) Block diagram (of the system) S 1 H 1 S 2

Basic logic functions - 17 Disjunction (OR function) Truth table example S 1 S 2 H 1 0 0 1 1 generally I 1 I 2 O 0 1 0 0 1 1
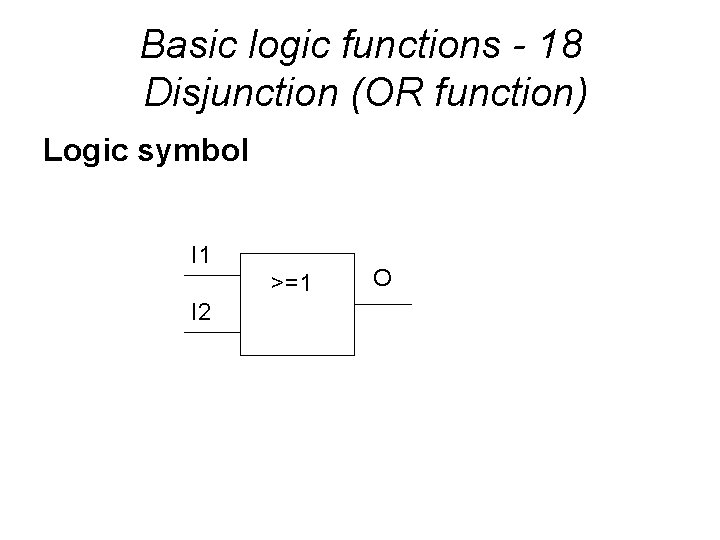
Basic logic functions - 18 Disjunction (OR function) Logic symbol I 1 >=1 I 2 O

Basic logic functions – 19 Disjunction (OR function) Important equations a+0=a a+1=1 a+a=a a + Na = 1

3. 2 Further logic operations various realisations The electrical realisation of a NOT -/AND/OR-operation has already been described in previous. Each of these operations can of course also be realised pneumatically or electronically. Boolean algebra also recognises the following logic operations. The following tables provide an overview of these.

Further logic operations various realisations -2

Further logic operations various realisations -3

3. 3 Establishing switching functions Deriving boolean equations from the truth table Often, the basic logic operations shown in the previous section are not enough to adequately describe a function in control technology. Very often, there is a combination of different logic operations. The logic connection in the form of a boolean equation can be easily established from the truth table. The example below should clarify this:

Establishing switching functions-2 Example: Sorting station task Various parts for built-in kitchens are to be machined in a production system (milling and drilling machine). The wall and door sections for certain types of kitchen are to be provided with different drill holes. Sensors B 1 to B 4 are intended for the detection of the holes.
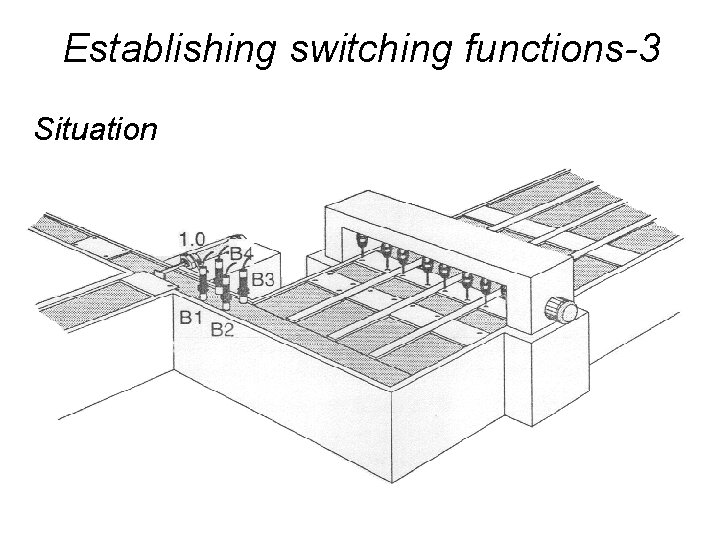
Establishing switching functions-3 Situation

Establishing switching functions-4 • Parts with the following hole patterns are for the 'Standard' kitchen type. These parts are to be advanced via the double-acting cylinder 1. 0. • Technological process Logical variable B 1 a B 2 b B 3 c B 4 d --------------------------------1. 0 y
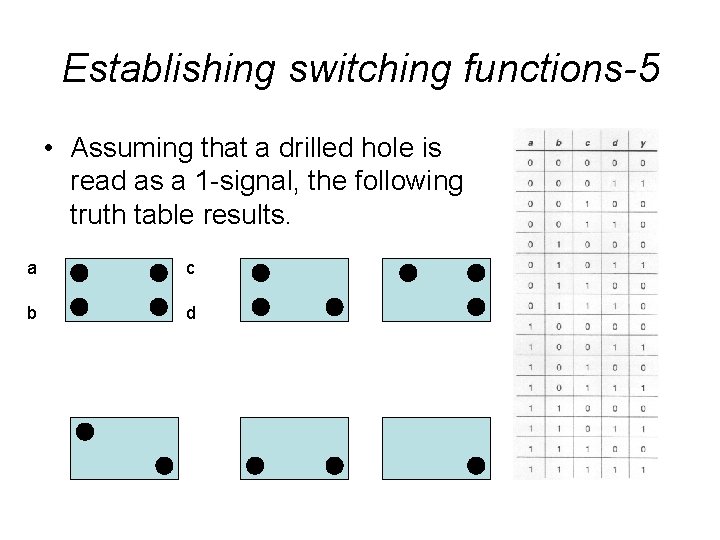
Establishing switching functions-5 • Assuming that a drilled hole is read as a 1 -signal, the following truth table results. a c b d

Establishing switching functions-6 • Two options (Standard form disjunctive and Standard form conjunctive) are available in order to derive the logic equation from this table, which lead to two different expressions. • The same result is obtained, of course, since the same circumstances are described.

Establishing switching functions-7 • Standard form, disjunctive In the disjunctive standard form, all conjunctions (AND-operations) of input variables with the result 1, are carried out as a disjunctive operation (OR-operation). With signal status 0, the input variable is carried out as a negated one and with signal status 1 as a non-negated one. disjunction of minterms

Establishing switching functions-8 • In the case of the example given, the logic function is therefore as follows: y=a. b. c. d+a. b. Nc. d+a. Nb. Nc. d+ +Na. b. Nc. d+Na. Nb. Nc. d Negated variable x (complement of x)……………Nx non-negated variable x ………………. . …x

Establishing switching functions-9 Standard form, conjunctive In the conjunctive standard form, all disjunctions (OR-operations) of the input variable producing the result 0, are carried out as a conjunctive operation (AND-operation). In contrast with the disjunctive standard form, in this instance, the input variable is negated with signal status "1" and a non-negated operation carried out with signal status „ 0". conjunction of maxterms

Establishing switching functions-10 logic function is therefore as follows: y=(a+b+c+d). (a+b+Nc+Nd). (a+Nb+c+d). (a+Nb+Nc+Nd). (Na+b+c+d). (Na+b+Nc+d). (Na+Nb+Nc+d).

3. 4 Simplification of logic functions • Both equations for the example given are rather extensive • Standard form disjunctive – more clear, shorter • Standard form conjunctive – here very long • Criteria for using the disjunctive form or conjunctive form: the decision is made in favour of the shorter form of the equation • In this case disjunctive form is better (shorter)

Simplification methods • The aim of the simplification is to shorten the total number of the literals (variables in true form …a, b, . . or variables in complemented form …Na, Nb…. ) and total number of logical operators (OR, AND, …) in the logical equation • Two methods are usually used: – Boolean algebra – Karnaugh map (application of Boolean algebra rules in a special way)

Postulates of Boolean algebra Definition: A set B of elements (a, b, c, …. ) with an equivalence relation (denoted =), two binary operations, one of them denoted by + (disjunction) and the other denoted by. (conjunction) and a unary operation, complementation (denoted by ‘ or N) is a Boolean algebra if and only if the following postulates are satisfied:

Postulates of Boolean algebra-2 • P 1 Associativity: The + and. operations are associative (a+b)+c=a+(b+c)=a+b+c (a. b). c=a. (b. c)=a. b. c • P 2 Commutativity: The + and. operations are associative a+b=b+a a. b=b. a

Postulates of Boolean algebra -3 • P 3 Distributivity: The two operations are distributive over each other a+b. c=(a+b). (a+c) a. (b+c)=a. b+a. c

Postulates of Boolean algebra-4 • P 4 Identity elements: There exists an identity element (denoted by 0, called zero) for the + operation and another (denoted by 1 and called one ore unity) for the. operation within B such that a+0=a a. 1=a

Postulates of Boolean algebra-5 • P 5 Complement Each member of B has a complement within B such that if a’ (Na) is the complement of a, then a+Na=1 a. Na=0

Postulates of Boolean algebra-6 It should be noted that 0 and 1, which denote two identity elements of the Boolean algebra, should not be misinterpreted as the numbers 0 and 1 of the ordinary algebra. It should also be mentioned here that as in ordinary algebra, so also in a Boolean algebra, the. operation is performed before the + operation! (priority) Thus a+b. c=a+(b. c)=/ (a+b). c

Fundamental theorems of Boolean algebra-1 • T 1 Closure of Identity Elements For all a e B a+1=1 a. 0=0 • T 2 Equality Theorem For all a, b, c e B if a+b=a+c and a. b=a. c, then b=c

Fundamental theorems of Boolean algebra-2 • T 3 Complementarity Theorem For all a, b e B if a+b=1 and a. b=0, then a=Nb and b=Na T 4 The identity elements 0 and 1 are complements of each other 0=N 1 and 1=N 0

Uniqueness properties of Boolean algebra • T 5 The identity elements 0 and 1 are unique. • T 6 The complement of an element is unique Bounds of Boolean algebra

Laws of Boolean algebra-1 • T 7 the law of involution For all a e B, N(Na)=a • T 8 the law of idempotence For all a e B, a+a=a and a. a=a • T 9 the law of absorption For all a, b a+a. b=a and a(a+b)=a

Laws of Boolean algebra-2 • T 10 De. Morgan’s theorem N(a+b)=Na. Nb N(a. b)=Na+Nb • T 11 Bounds of Boolean algebra Identity elements 0 and 1 constitute the lower and upper bouds respectivelly for all the elements of a Boolean algebra.

Laws of Boolean algebra-3 • T 12 Duality in Boolean algebra Every theorem in Boolean algebra has its dual, which is also true. Notice, that all five postulates that form the basis of Boolean algebra is presented in a pair of equations. An important property exhibited by the pairs is that one element of a pair can be obtained from the other by interchanging the + and. Operations and the identity elements 0 and 1. This property is known as the principle of duality and one of the pair of equations is called the dual of the other.

Two-valued Boolean algebra • There also for example eight-valued and four-valued Boolean algebra. In industrial control, PLCs and PCs we usually use two-valued , so called switching algebra

Simplification using Boolean algebra (previous example)-1 y=Na. Nb. Nc. d+Na. b. Nc. d+a. Nb. c. d+ +a. b. Nc. d+ a. b. c. d= =Na. Nb. Nc. d+Na. b. Nc. d+a. Nb. c. d+ +a. b. d. (Nc+ c)= =Na. Nb. Nc. d+Na. b. Nc. d+a. Nb. c. d+ +a. b. d= Na. Nc. d(Nb+b)+a. Nb. d(Nc+c)+ a. b. d= = Na. Nc. d+ a. Nb. d+ a. b. d=

Simplification using Boolean algebra (previous example)-2 = Na. Nc. d+ a. Nb. d+ a. b. d= = Na. Nc. d+ a. d(Nb + b) = = Na. Nc. d+ a. d = =d. (Na. Nc+a)= /absorption of negation/ =d(Nc+a)= = Nc. d+a. d

Simplification using Boolean algebra (previous example)-3 Absorption of negation • a+Na. b=a+b • Na+a. b=Na+b • a. (Na+b)=a. b • Na. (a+b)=Na. b

Simplification using Boolean algebra (previous example)-4 • The basic principle of simplification is the factoring out of variables and reducing to defined expressions. • However this method does require a sound knowledge of Boolean algorithms plus a certain amount of practice. • Another option for simplification will be introduced in the following section (Karnaugh map)

3. 5 Karnaugh-Veitch diagram Karnaugh map • The truth table has 16 rows ( 2 powered by 3, 3 is number of variables) • The related Karnaugh map must have 16 positions for function values (eg. 4 x 4) • Each position in K-map has its index (binary value related to the value of input variables combinations) • Index has values from 0 to 15
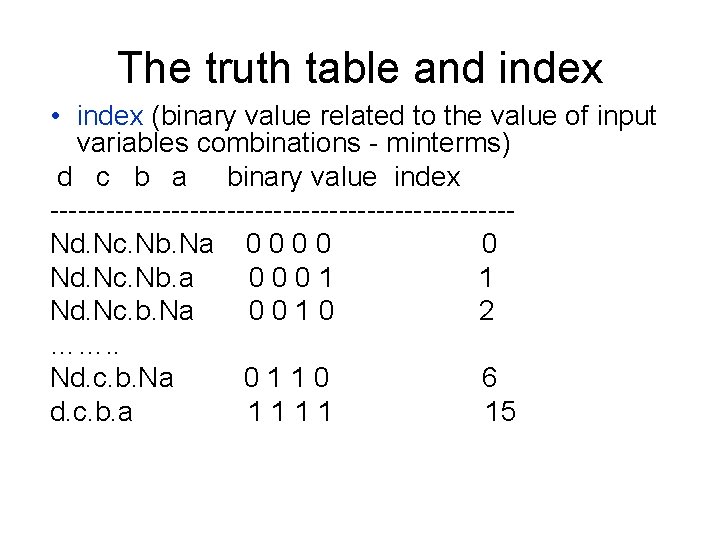
The truth table and index • index (binary value related to the value of input variables combinations - minterms) d c b a binary value index -------------------------Nd. Nc. Nb. Na 0 0 0 Nd. Nc. Nb. a 0001 1 Nd. Nc. b. Na 0010 2 ……. . Nd. c. b. Na 0110 6 d. c. b. a 1111 15
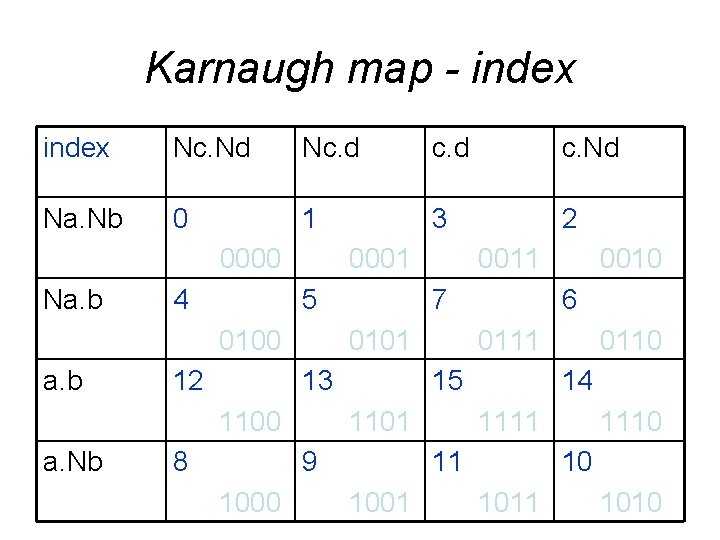
Karnaugh map - index Nc. Nd Nc. d c. Nd Na. Nb 0 1 3 2 0000 Na. b 4 0001 5 0100 a. b 12 7 0101 13 1100 a. Nb 8 0111 1101 0110 14 1111 11 1001 0010 6 15 9 1000 0011 1110 10 1011 1010
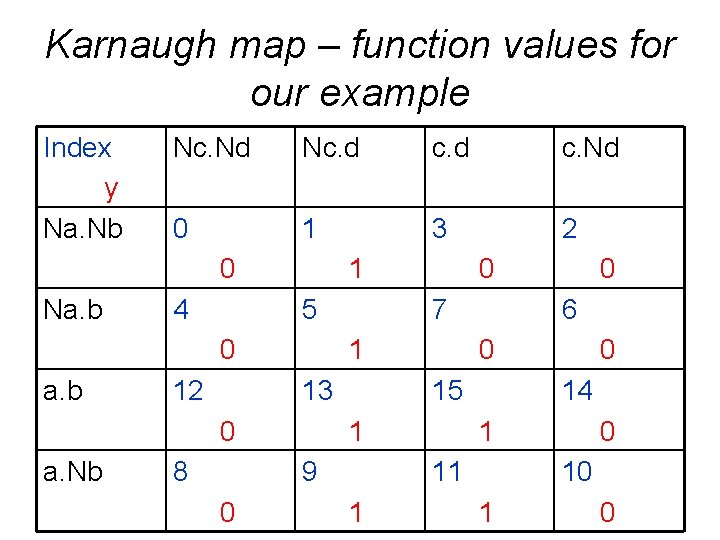
Karnaugh map – function values for our example Index y Na. Nb Nc. Nd Nc. d c. Nd 0 1 3 2 0 Na. b 4 1 5 0 a. b 12 7 1 13 0 a. Nb 8 0 14 1 11 1 0 6 15 9 0 0 0 10 1 0
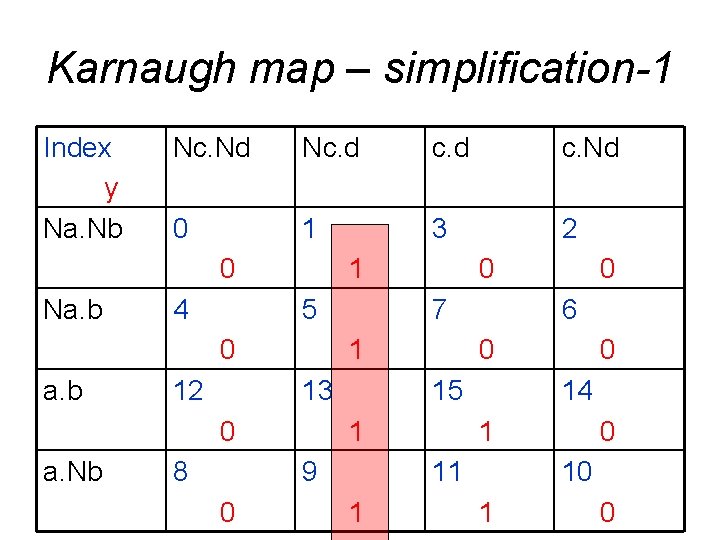
Karnaugh map – simplification-1 Index y Na. Nb Nc. Nd Nc. d c. Nd 0 1 3 2 0 Na. b 4 1 5 0 a. b 12 7 1 13 0 a. Nb 8 0 14 1 11 1 0 6 15 9 0 0 0 10 1 0

Karnaugh map – simplification-2 What variable values are common for all this rectangular ? Nc. d
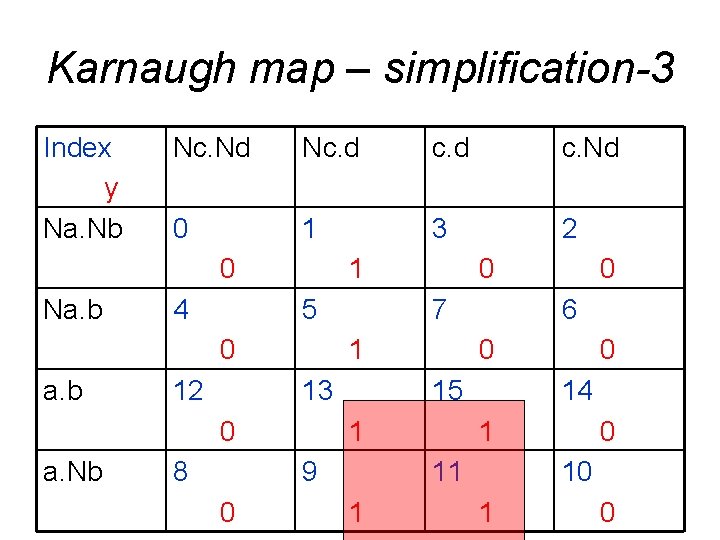
Karnaugh map – simplification-3 Index y Na. Nb Nc. Nd Nc. d c. Nd 0 1 3 2 0 Na. b 4 1 5 0 a. b 12 7 1 13 0 a. Nb 8 0 14 1 11 1 0 6 15 9 0 0 0 10 1 0
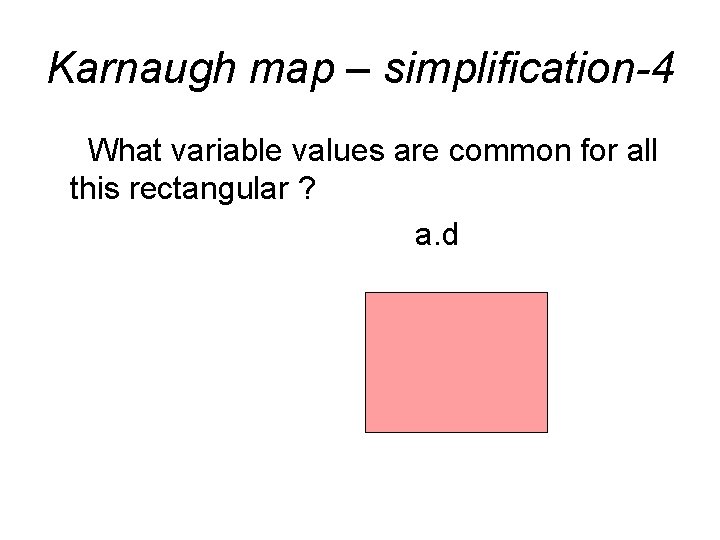
Karnaugh map – simplification-4 What variable values are common for all this rectangular ? a. d
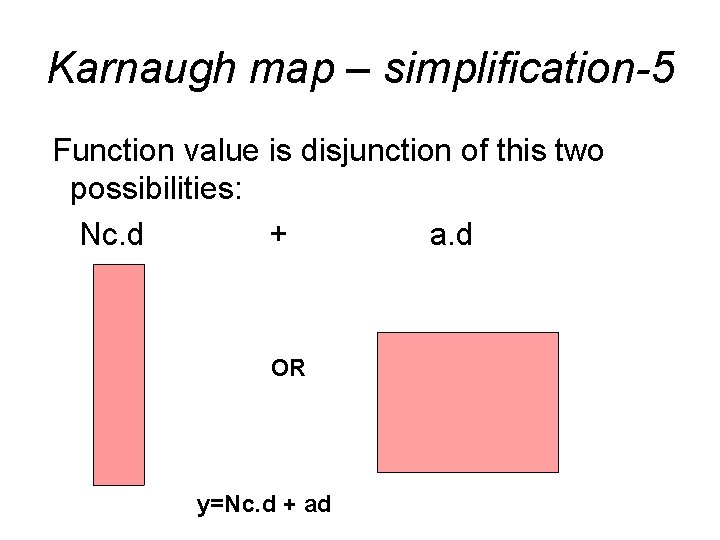
Karnaugh map – simplification-5 Function value is disjunction of this two possibilities: Nc. d + a. d OR y=Nc. d + ad

Karnaugh map – simplification-6 • The combining statuses in the K-map must be in the form of a rectangle or a square • The number of combining statuses must be a result of 2 power by x • All „ones“ from the K-map must have related minterm in the resulting simplified function • „one“ from the K-map can be used repeatly for a minterm

Literature • Nripendra N. Biswas: Logic Design Theory, Prentice Hall International, 1993, ISBN 0 -13 -010695 -X
- Slides: 63