Lecture 3 2 6 Fundamental Gaussian Beams in

Lecture 3 § 2. 6 Fundamental Gaussian Beams in a Lenslike Medium

§ 2. 6 Fundamental Gaussian Beams in a Lenslike Medium So that, w (z) is the beam spot size and R its radius of curvature, as in the case of a homogeneous medium.

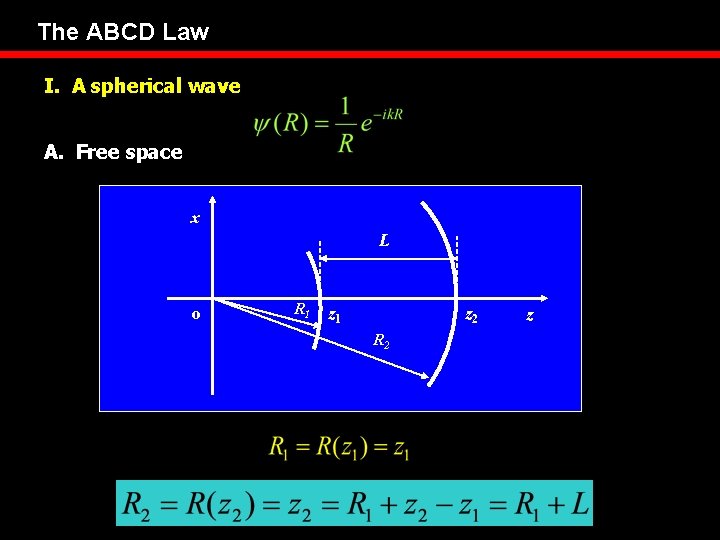
The ABCD Law I. A spherical wave A. Free space x L o R 1 z 2 R 2 z

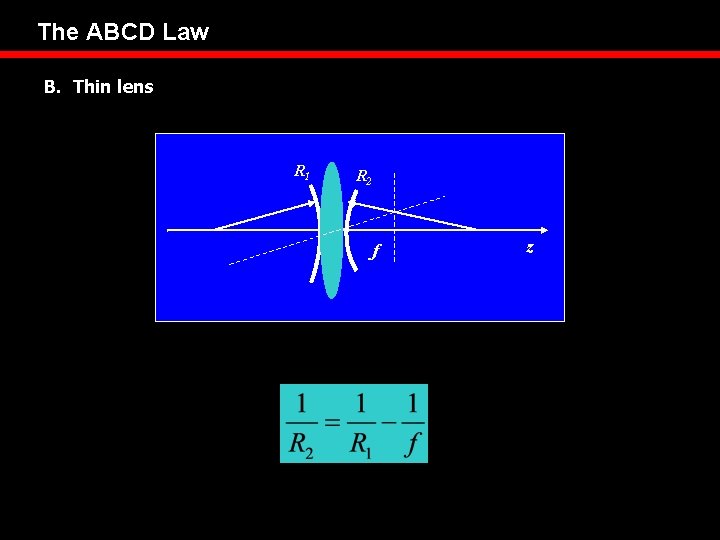
The ABCD Law B. Thin lens R 1 R 2 z 1 f z

The ABCD Law Ray Matrices So, for the spherical wave, we have: ABCD express

The ABCD Law A. Free space Compare to a spherical wave:

The ABCD Law B. Thin lens (1) 由 Boyd-Gordon 理论可知高斯光束通过薄透镜后仍为高斯光束。 (2) q is complex radius of curvature of the Gaussian beam

The ABCD Law C. Two thin lenses sequence First Lens Second Lens D. Above conclusion can be expanded to the multiple optical elements

Exercise: Gaussian Beam Focusing 2 w 0 z 1 f Characteristic the beam focusing status. The smaller the z 0 , the stronger the focusing, but less depth of focusing 2 L 3

Exercise: Gaussian Beam Focusing 2 wf 2 w 0 z z f Geometric Optics f Gaussian Optics Focus at focus point Depth of foucs Spot size independent on input beam size, just a point spot. Physical Optics Diffraction limit:

§ 2. 7 A Gaussian Beam in Lens Waveguide d d … z f 1 f 2 f 1 …

§ 2. 7 A Gaussian Beam in Lens Waveguide The condition for the confinement of the Gaussian beam by the lens sequence is that be real; otherwise, the sine function will yield growing exponentials. This condition becomes: or The same as Ray case

§ 2. 8 High-order Gaussian Beam Modes in a Homogeneous medium

§ 2. 8 High-order Gaussian Beam Modes in a Homogeneous medium Longitudinal phase shift: When l=m=0, it reduces to the results of fundamental Gaussian mode Transverse variation: Well-known harmonic oscillator wavefunction, Hl is the Hermite polynomial of order l Transverse phase shift: The same as fundamental Gaussian mode

§ 2. 8 High-order Gaussian Beam Modes in a Homogeneous medium l=0 l=3 l=10 l=2 Note: the node points and the peak intensity variations at different l

§ 2. 8 High-order Gaussian Beam Modes in a Homogeneous medium TEMlm x direction has (l+1) bright spots or l dark spots y direction has (m+1) bright spots or m dark spots

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media I. The modes of Gaussian Beam In previous sections, we treated the propagation of a circularly symmetric Gaussian beam in lenslike media. Here we extend the treatment to higherorder modes and limit our attention to steady state (q(z)=const. ) solutions in medium whose index refraction can be described by:

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media Well-known harmonic oscillator Schwinger equation. Eigen value: Eigen function:

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media Eigen value: Eigen function: Spot size:

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media Notes: A. Unlike the homogenous medium, the mode spot size is independent of z; focusing action counteracts the natural spread (n 2> 0), however, no confined solution exist for n 2<0 B. The propagation constant b depends on mode indices l, m causes the different modes to have phase velocities vl, m=w/bl, m and group (vg)l, m=dw/dbl, m velocities that depend on l and m.

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media II. Modal Dispersion of Group Velocity

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media III. Pulse Spreading in Quadratic Index Glass Fibers Glass fibers with quadratic index profiles are excellent channels for optical communication system. The information is coded into trains of optical pulse and the channel information capacity is thus fundamentally limited by the number of pulses that can be transmitted per unit time. A. Modal Dispersion The maximum pulses number per second

§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media t t Dt t Students Exercise: t

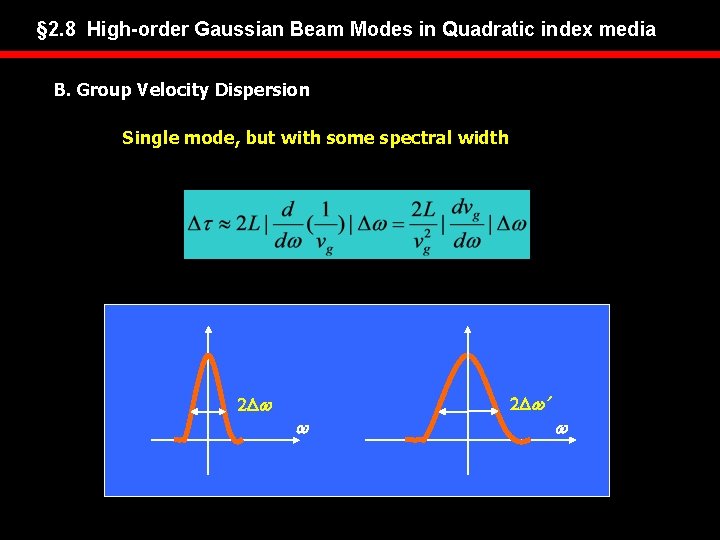
§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media B. Group Velocity Dispersion Single mode, but with some spectral width 2 Dw w 2 Dw’ w

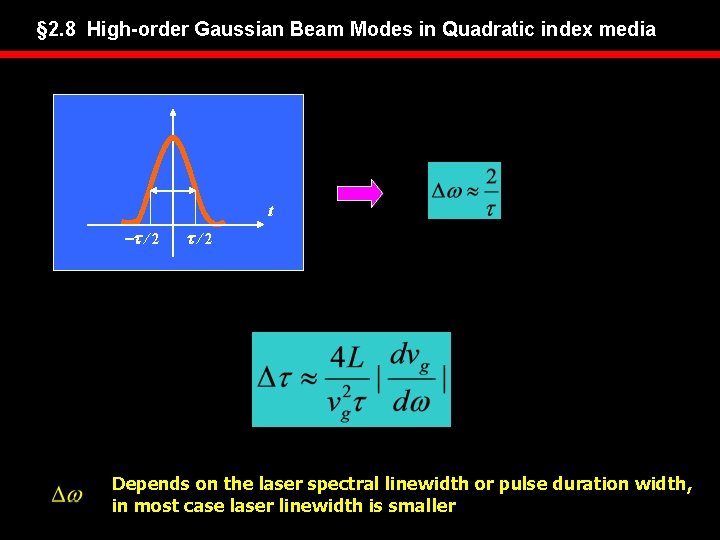
§ 2. 8 High-order Gaussian Beam Modes in Quadratic index media t -t / 2 t/2 Depends on the laser spectral linewidth or pulse duration width, in most case laser linewidth is smaller

§ 2. 9 Propagation in Media with Quadratic Gain Profile Gain is a strong function of position: (1) The radial distribution of energetic electrons in the plasma region of gas lasers; (2) The variation of pumping intensity in solid state lasers; (3) The dependence of the degree of gain saturation on the radial position of the beam.

§ 2. 9 Propagation in Media with Quadratic Gain Profile For steady-state solution: For non-steady-state solution:

Homework 章节后习题 2. 8、2. 9、2. 12.