Lecture 3 0 Structural Defects Mechanical Properties of

Lecture 3. 0 Structural Defects Mechanical Properties of Solids

Defects in Crystal Structure l Vacancy, Interstitial, Impurity l Schottky Defect l Frenkel Defect l Dislocations – edge dislocation, line, screw l Grain Boundary

Substitutional Impurities Interstitial Impurities

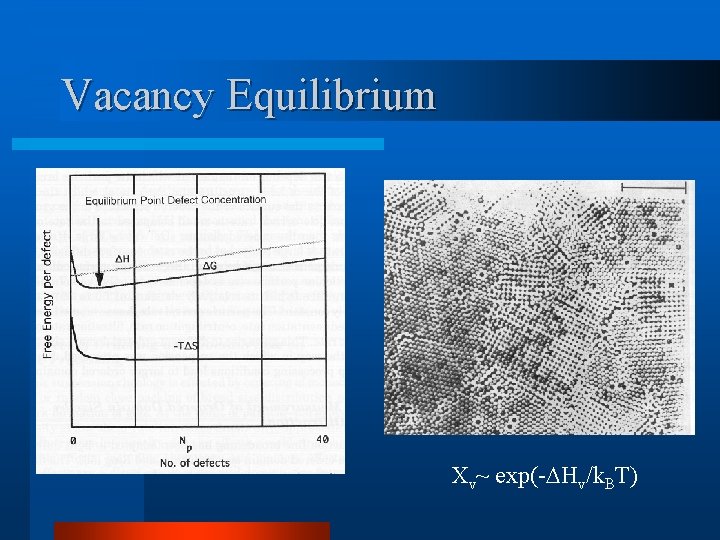
Self Interstitial Vacancy Xv~ exp(- Hv/k. BT)

Vacancy Equilibrium Xv~ exp(- Hv/k. BT)

Defect Equilibrium Sc= k. Bln gc(E) Sb= k. Bln Wb Entropy Ss= k. Bln Ws d. Fc = d. E-Td. Sc-Td. Ss, the change in free energy d. Fc ~ 6 nearest neighbour bond energies (since break on average 1/2 the bonds in the surface) Wb=(N+n)!/(N!n!) ~(N+n+1)/(n+1) ~(N+n)/n (If one vacancy added) d. Sb=k. Bln((N+n)/n) For large crystals d. Ss<<d. Sb n ~ N exp –d. Fc/k. BT

Ionic Crystals Shottky Defect Frenkel Defect

Edge Dislocation

Grain Boundaries

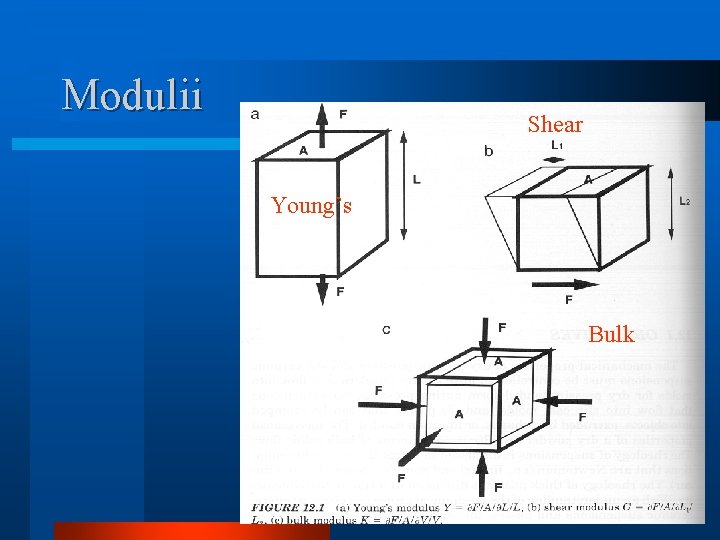
Mechanical Properties of Solids l Elastic deformation – reversible • Young’s Modulus • Shear Modulus • Bulk Modulus l Plastic Deformation – irreversible • change in shape of grains l Rupture/Fracture

Modulii Shear Young’s Bulk

Mechanical Properties Stress, xx= Fxx/A l Shear Stress, xy= Fxy/A l Compression l l Yield Stress – yield ~Y/10 – yield~G/6 (theory-all atoms to move together) Strain, = x/xo l Shear Strain, = y/xo l l Volume Strain = V/Vo l Brittle Fracture – stress leads to crack – stress concentration at crack tip =2 (l/r) – Vcrack= Vsound

Effect of Structure on Mechanical Properties l Elasticity l Plastic Deformation l Fracture

Elastic Deformation l Pulling on a wire decreases its diameter – l/lo= - l/Ro l Poisson’s l Young’s Modulus – Y(or E)= (F/A)/( l/lo) l Shear Modulus – G= / = Y/(2(1+ )) Ratio, l Bulk Modulus 0. 5 (liquid case=0. 5) • K=-P/( V/Vo) • K=Y/(3(1 -2 ))

Microscopic Elastic Deformation Interatomic Forces l FT =Tensile Force l FC=Compressive Force l Note F=d(Energy)/dr l

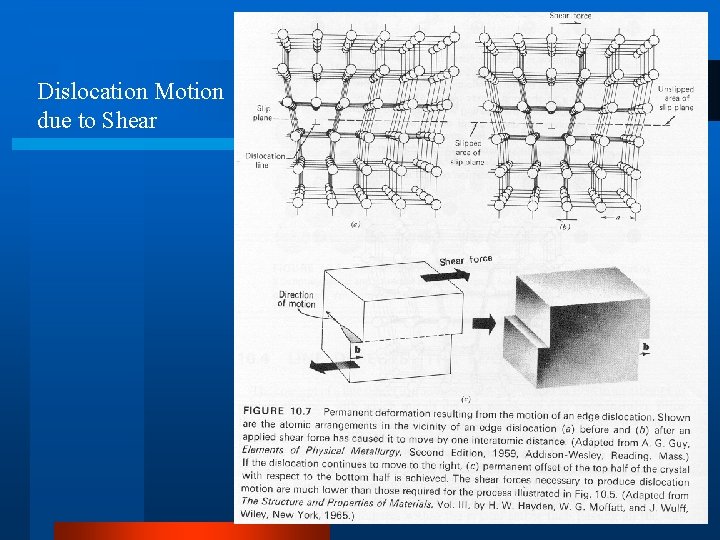
Plastic Deformation l Single Crystal – by slip on slip planes Shear Stress

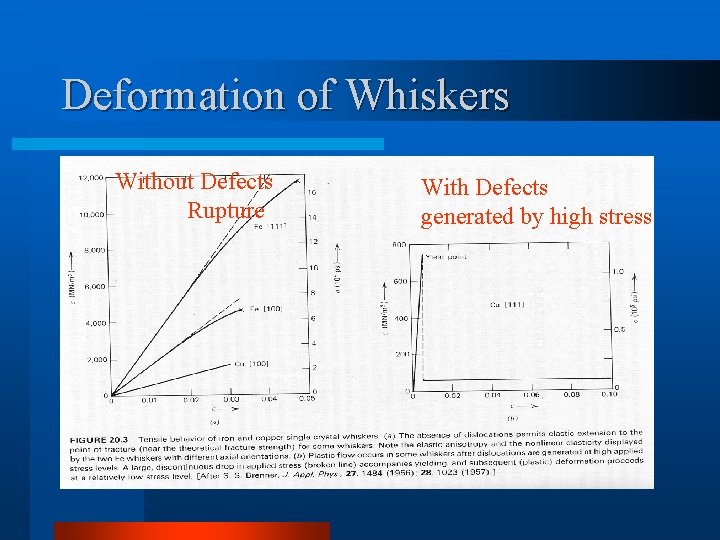
Deformation of Whiskers Without Defects Rupture With Defects generated by high stress

Dislocation Motion due to Shear

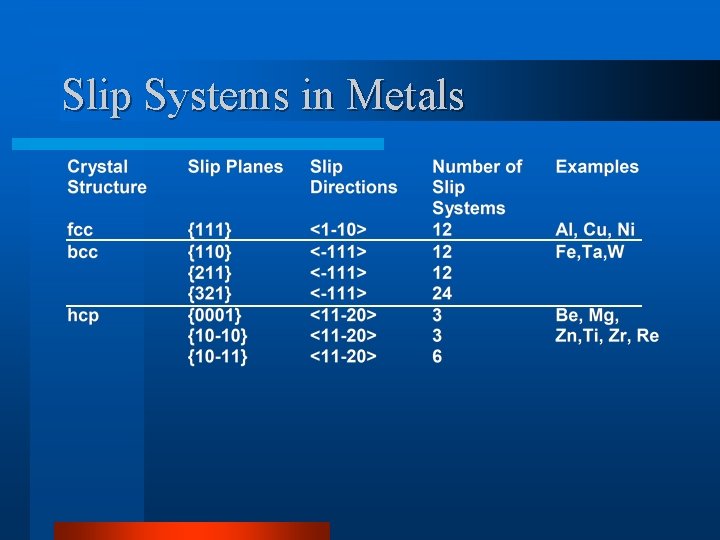
Slip Systems in Metals

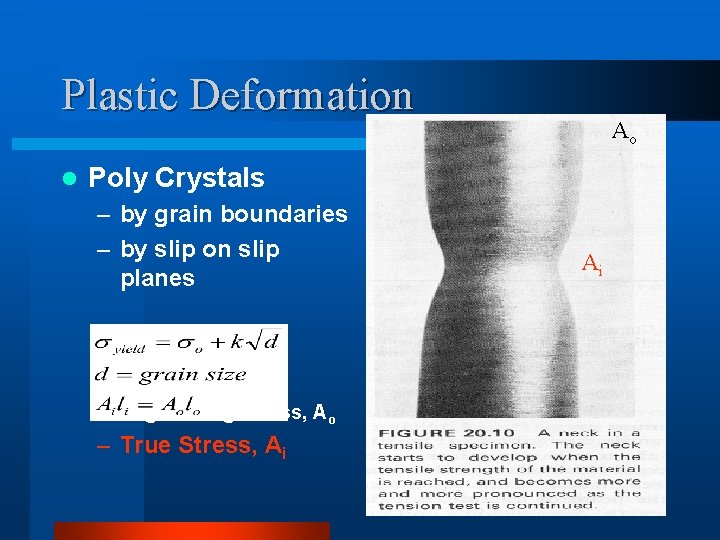
Plastic Deformation l Ao Poly Crystals – by grain boundaries – by slip on slip planes – Engineering Stress, Ao – True Stress, Ai Ai

Movement at Edge Dislocation Slip Plane is the plane on which the dislocation glides Slip plane is defined by BV and I

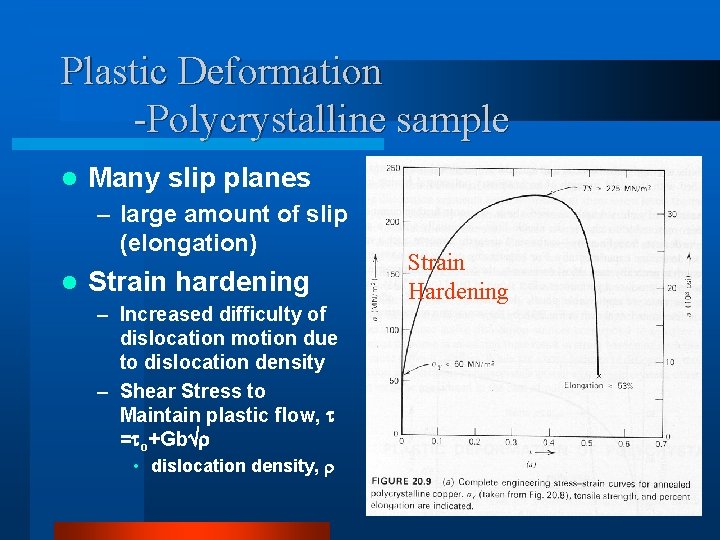
Plastic Deformation -Polycrystalline sample l Many slip planes – large amount of slip (elongation) l Strain hardening – Increased difficulty of dislocation motion due to dislocation density – Shear Stress to Maintain plastic flow, = o+Gb • dislocation density, Strain Hardening

Strain Hardening/Work Hardening l Dislocation Movement forms dislocation loops – New dislocations created by dislocation movement Critical shear stress that will activate a dislocation source l c~2 Gb/l l – G=Shear Modulus – b=Burgers Vector – l=length of dislocation segment

Depends on Grain Size

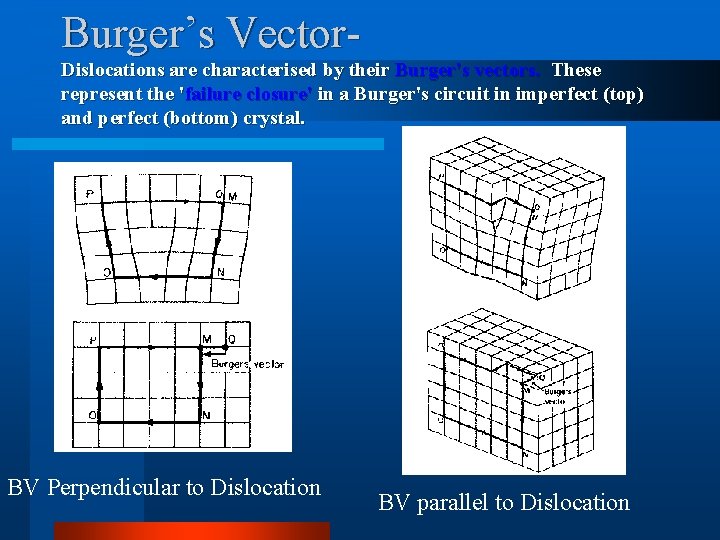
Burger’s Vector. Dislocations are characterised by their Burger's vectors. These represent the 'failure closure' in a Burger's circuit in imperfect (top) and perfect (bottom) crystal. BV Perpendicular to Dislocation BV parallel to Dislocation

Solution Hardening (Alloying) l Solid Solutions • Solute atoms segregate to dislocations = reduces dislocation mobility • higher required to move dislocation – Solute Properties • larger cation size=large lattice strain • large effective elastic modulus, Y l Multi-phase alloys - Volume fraction rule

Precipitation Hardening l Fine dispersion of heterogeneity • impede dislocation motion – c~2 Gb/ • is the distance between particles – Particle Properties • very small and well dispersed • Hard particles/ soft metal matrix l Methods to Produce – Oxidation of a metal – Add Fibers - Fiber Composites

Cracking vs Plastic Deformation l Brittle l • Poor dislocation motion • stress needed to initiate a crack is low • good dislocation motion • stress needed to initiate slip is low – Ionic Solids – Metals • disrupt charges • electrons free to move – Covalent Solids • disrupt bonds – Amorphous solids • no dislocations Ductile l Depends on T and P – ductile at high T (and P)