Lecture 29 Oscillation linear superposition and wave Oscillations












- Slides: 16

Lecture 29 Oscillation, linear superposition, and wave • Oscillations of couple oscillators • General properties of linear system (Chpt 23) • Oscillations of many particles: wave • Vibration in Solids and sound wave • Feynman Chpt 25, Chpt 49. 4, 49. 5 1

Simple oscillation and many oscillation 2

Coupled springs (oscillation of two particles) • Two particles connected by three springs k m k x 1 • (1)±(2) x 2 normal coordinates normal frequencies 3

The most general motion of a system is a superposition of its normal modes The modes are normal in the sense that they can move independently, that is to say that an excitation of one mode will never cause motion of a different mode. In mathematical terms, normal modes are orthogonal to each other. 4

Find the normal modes 5

General properties of linear systems: superposition principle • 6

More general case of superposition 7

Normal modes (49. 5) 8

More springs and more particles • Java applet http: //www. falstad. com/coupled/ • In this case, there are three linear differential equations, three normal modes 9

Oscillation of many particles: Waves! Difference modes: Characterized by “Wavelength” Separation of particles repeating itself and Oscillation frequency 10


Waves • A wave is disturbance or oscillation (of a physical quantity), that travels through matter or space, accompanied by a transfer of energy. • Mechanical waves propagate through a medium, and the substance of this medium is deformed. The deformation reverses itself owing to restoring forces resulting from its deformation. • Electromagnetic waves, do not require a medium. Instead, they consist of periodic oscillations of electrical and magnetic fields generated by charged particles, and can therefore travel through a vacuum. • Matter wave (quantum mechanics) • Gravitational wave are ripples in the curvature of spacetime that propagate as a wave, travelling outward from the source. 12

Some examples 13

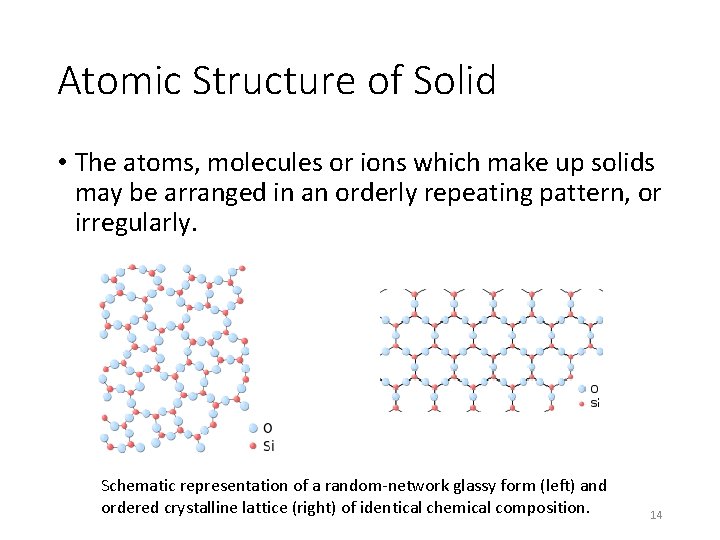
Atomic Structure of Solid • The atoms, molecules or ions which make up solids may be arranged in an orderly repeating pattern, or irregularly. Schematic representation of a random-network glassy form (left) and ordered crystalline lattice (right) of identical chemical composition. 14

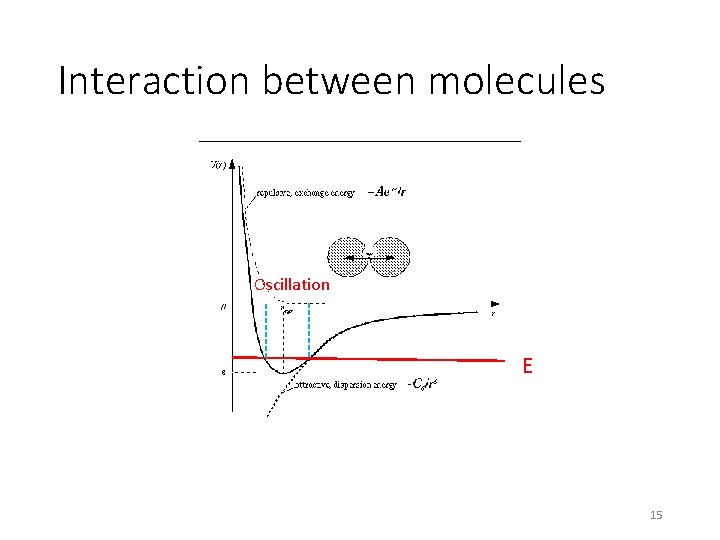
Interaction between molecules Oscillation E 15

Sound wave in Solids • In solids their atoms vibrate about fixed mean positions within the ordered (or disordered) lattice. • The spectrum of lattice vibrations in a crystalline or glassy network provides the foundation for the kinetic theory of solids. • This motion occurs at the atomic level, and thus cannot be observed or detected without highly specialized equipment, such as that used in spectroscopy. 16