Lecture 29 ECE 743 3 Phase Induction Machines

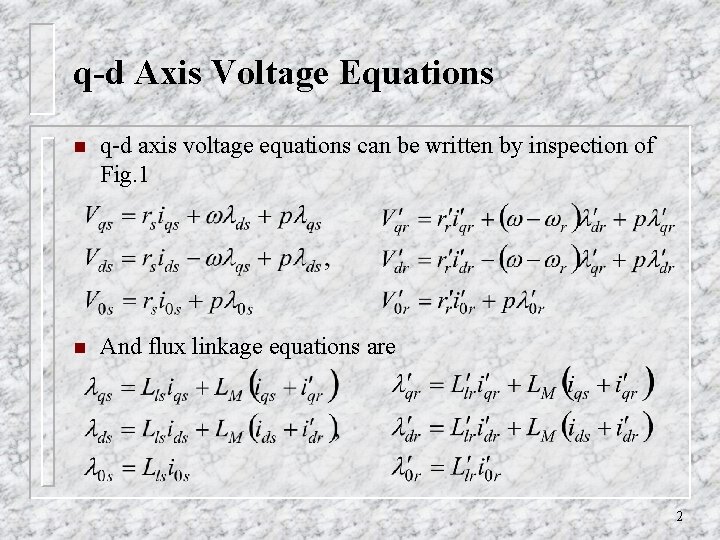












- Slides: 20

Lecture 29 - ECE 743 3 -Phase Induction Machines Reference Frame Theory – Part IV Professor: Ali Keyhani
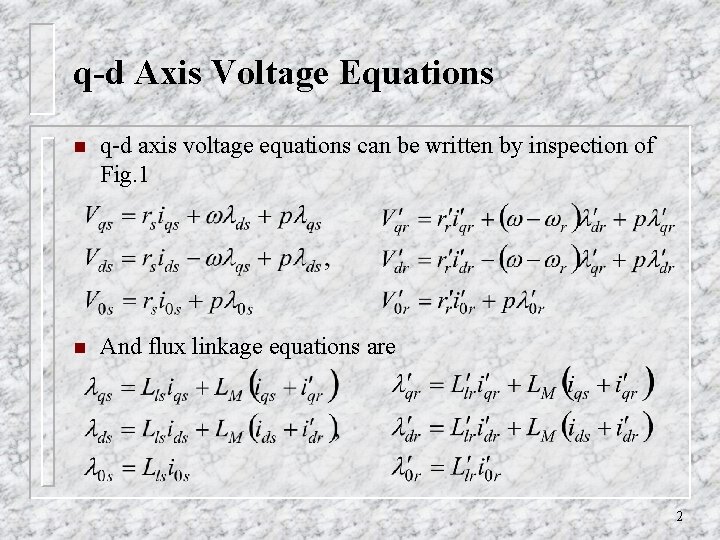
q-d Axis Voltage Equations n q-d axis voltage equations can be written by inspection of Fig. 1 n And flux linkage equations are 2

q-d Axis Voltage Equations Fig. 1 Axis of 2 -pole, 3 -phase symmetrical induction. 3

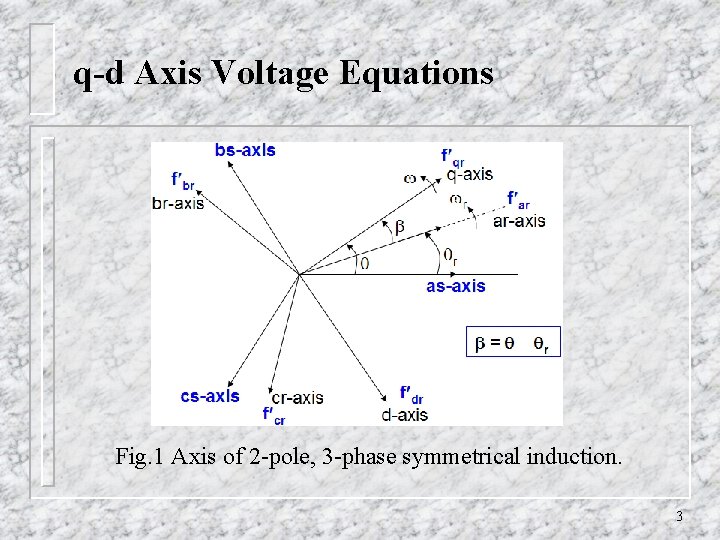
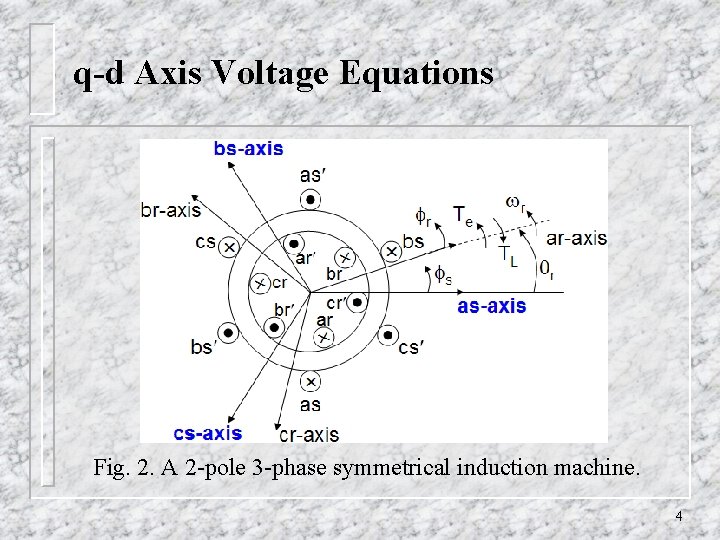
q-d Axis Voltage Equations Fig. 2. A 2 -pole 3 -phase symmetrical induction machine. 4

q-d Axis Voltage Equations Fig. 2. A 2 -pole 3 -phase symmetrical induction machine. 5

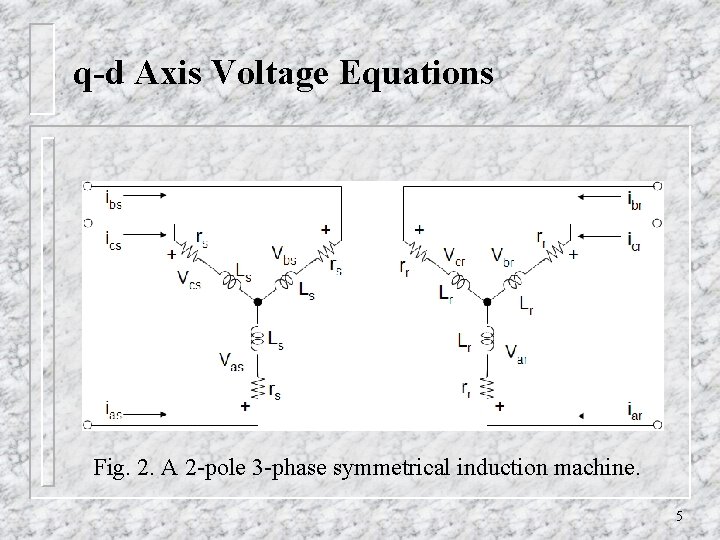
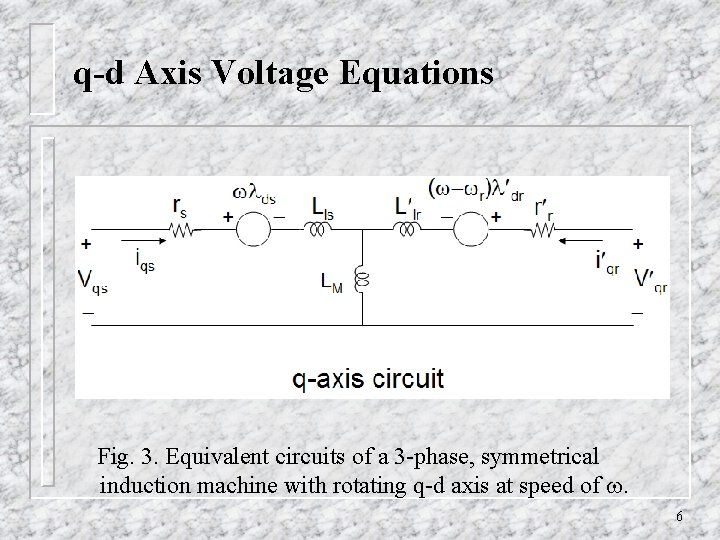
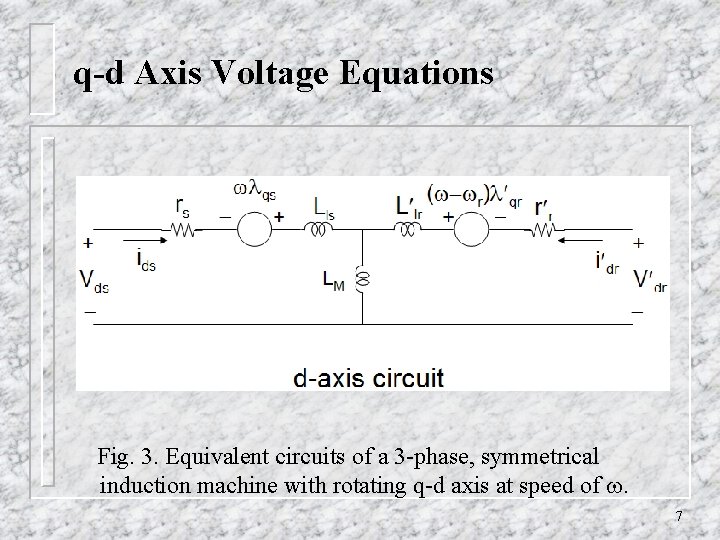
q-d Axis Voltage Equations Fig. 3. Equivalent circuits of a 3 -phase, symmetrical induction machine with rotating q-d axis at speed of . 6

q-d Axis Voltage Equations Fig. 3. Equivalent circuits of a 3 -phase, symmetrical induction machine with rotating q-d axis at speed of . 7

q-d Axis Voltage Equations Fig. 3. Equivalent circuits of a 3 -phase, symmetrical induction machine with rotating q-d axis at speed of . 8

q-d Axis Voltage Equations n When =0 (stationary reference frame), voltage equations become, n When = r (rotor reference frame) which is also referred to as Park’s transformation, voltage equations become, 9

q-d Axis Voltage Equations n When = e (synchronously rotating reference frame), the voltage equations become, n Synchronously rotating reference frame is used when incorporating the dynamic characteristics od an induction machine into a digital computer program used to study the transient and dynamic stability of large power systems. Synchronously rotating reference frame is also used in variable frequency study of induction machines. n 10

Per Unit System n Machine data, - Stator line frequency: f (Hz) - Output horse power: HP (hp) - Line to line voltage: V (rms V) - Pole number: P n Base values, 11

Per Unit System n Base electrical angular velocity = b=2 fb rad/sec, Base mechanical angular velocity = brm=2 fb/(P/2) Let 12

Per Unit System n Define n Machine voltage equations in p. u can be written as 13

Per Unit System n Torque base 14

Per Unit System n Per unit equation of motion is n Define quantity 15

Per Unit System Therefore, J: kg. m 2 Pb: watts b: rad/sec 16

Per Unit System n The quantity H is called the inertia constant and has units of seconds. n: rpm KVA: base KVA J: kg. m 2 Wk 2: Lb-ft 2 17

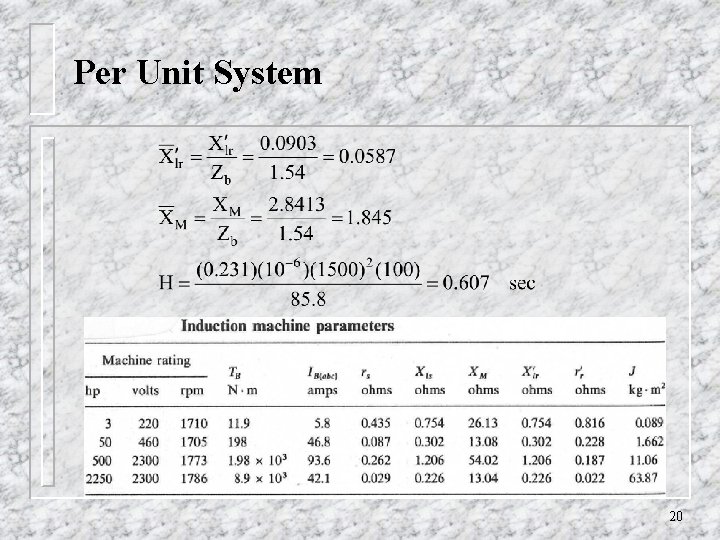
Per Unit System n Example HP = 115 Poles = 4 Vrated = 210 rms/phase f = 50 Hz (rated) J = 100 Lb-ft 2 rs = 0. 016 r r = 0. 001 Xls = 0. 0706 X lr = 0. 0903 X m = 2. 8413 - Base values Pb = (746)(115) = 85, 800 watts Vb = (210) 2 = 297 Volts peak Ib = (2/3)(Pb/Vb) = 193 Amp. peak Zb = (Vb/Ib) = (297/193) = 1. 54 18

Per Unit System - Base angular frequency = b = 2 (50) = 314 rad/sec - Torque base = Tb = [Pb(P/2)]/ b = 547 N-m 19

Per Unit System 20