Lecture 28 Review Frequency domain circuit analysis Superposition

Lecture 28 • Review: • Frequency domain circuit analysis • Superposition • Frequency domain system characterization • Frequency Response • Related educational materials: –Chapter 10. 5, 10. 6

• Note during summary that we will be changing our mindset, rather than doing anything fundamentally new – I will keep re-introducing the same example circuit, but with minor modifications and extensions

Frequency domain analysis – review • The analysis techniques we used for time domain analysis of resistive networks are applicable to frequency domain analysis of general circuits • E. g. KVL, KCL, circuit reduction, nodal analysis, mesh analysis, Thevenin’s and Norton’s Theorems… • In general, we simply need to: • Subsitute impedances for resistances • Use phasor voltages & currents in place of time domain voltages & currents

Superposition • Superposition in frequency domain: • If multiple signals exist at different frequencies, superposition is the only valid frequency domain approach • Effects of individual sources can be analyzed independently in the frequency domain • Summation of individual contributions must be done in the time domain (unless all contributions have same frequency)

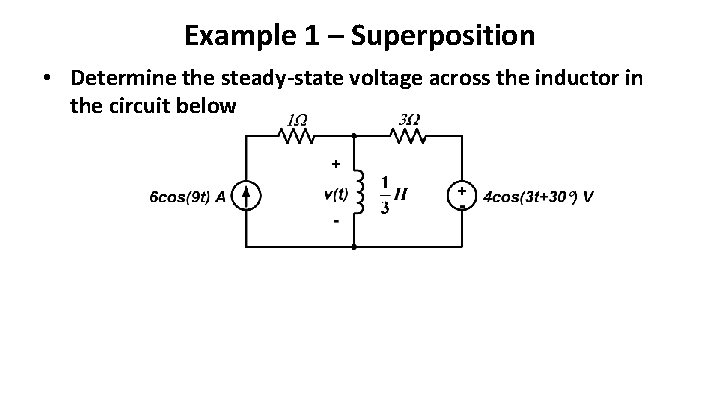
Example 1 – Superposition • Determine the steady-state voltage across the inductor in the circuit below

• In previous slide, show time domain superposition. V(t) = v 1(t) +v 2(t) – Note that we can determine v 1(t) and v 2(t) individually using frequency domain analysis – We can’t however, superimpose these individually, for reasons that will be made clear on the next slide

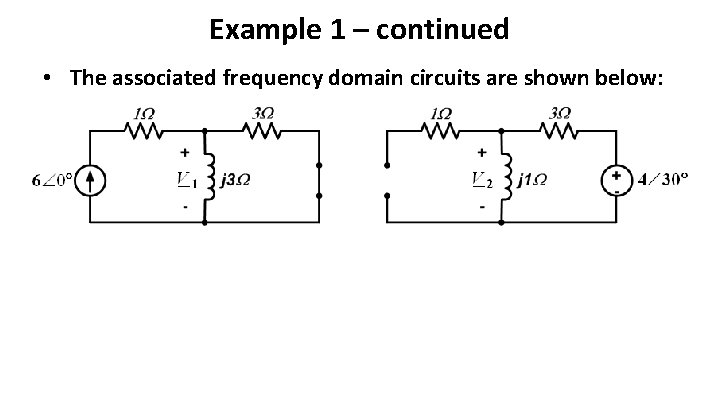
Example 1 – continued • The associated frequency domain circuits are shown below:

• Derive the phasors V 1 and V 2 on the previous slide • Point out that they can’t be added directly – they don’t even apply to the same frequency domain circuit – We will superimpose the results in the time domain

Example 1 – continued again • Superimpose results in the time domain:

• On previous slide, V 1 has frequency of 9 rad/sec and V 2 has frequency of 3 rad/sec

Notes on superposition • Superposition of sinusoidal signals is extremely important in circuit analysis! • In later courses, we will see that (nearly any) signal can be represented as a superposition of sinusoidal signals, using Fourier Series and Fourier Transforms • If we determine the circuit’s response to each of these sinusoids and superimpose them, we can determine the circuit’s response to (nearly any) input function • We will spend the next couple of lectures looking at circuit responses to multiple sinusoidal inputs

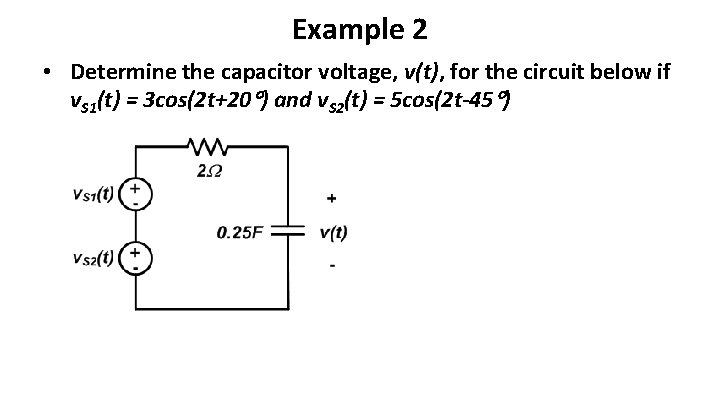
Example 2 • Determine the capacitor voltage, v(t), for the circuit below if v. S 1(t) = 3 cos(2 t+20 ) and v. S 2(t) = 5 cos(2 t-45 )

• On the previous chart, draw single-source circuit and point out that VS = vs 1+vs 2 and v(t)=v 1+v 2 – Draw two frequency-domain circuits ; note that they both have the same appearance

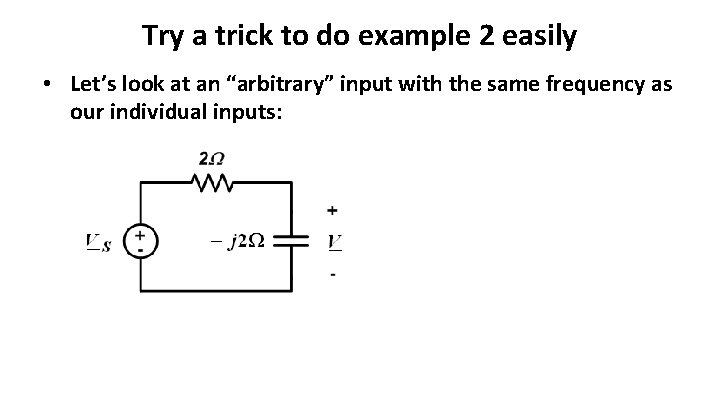
Try a trick to do example 2 easily • Let’s look at an “arbitrary” input with the same frequency as our individual inputs:

• Determine input-output relationship (gain, phase) => point out that this is only good for 2 rad/sec frequency sinusoids

Example 2 – continued • Now we can use our trick to easily determine the circuit’s response to both inputs (since they are at the same frequency)

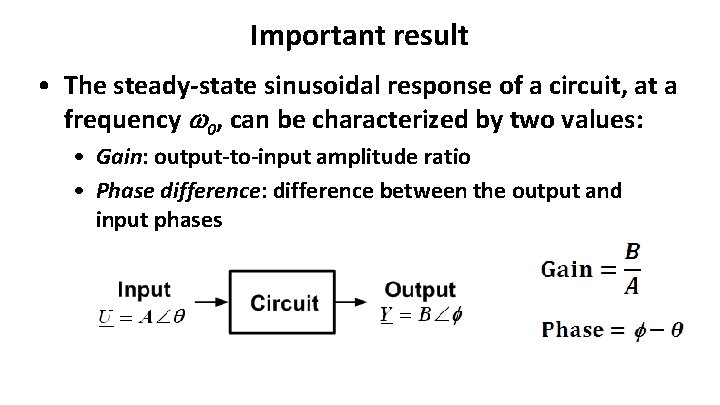
Important result • The steady-state sinusoidal response of a circuit, at a frequency 0, can be characterized by two values: • Gain: output-to-input amplitude ratio • Phase difference: difference between the output and input phases

• On previous slide, annotate output to show on block diagram: – Y = H*U, where H is a complex number that depends only on frequency – Circuit “looks like” H, at the frequency of interest

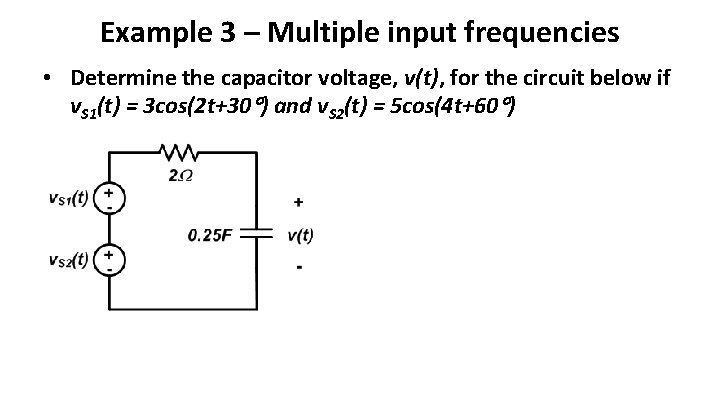
Example 3 – Multiple input frequencies • Determine the capacitor voltage, v(t), for the circuit below if v. S 1(t) = 3 cos(2 t+30 ) and v. S 2(t) = 5 cos(4 t+60 )

• Annotate slide to show two frequency-domain circuits; note that they have different frequency-domain characteristics – I don’t want to analyze two circuits, so let’s leave frequency in the circuit model!

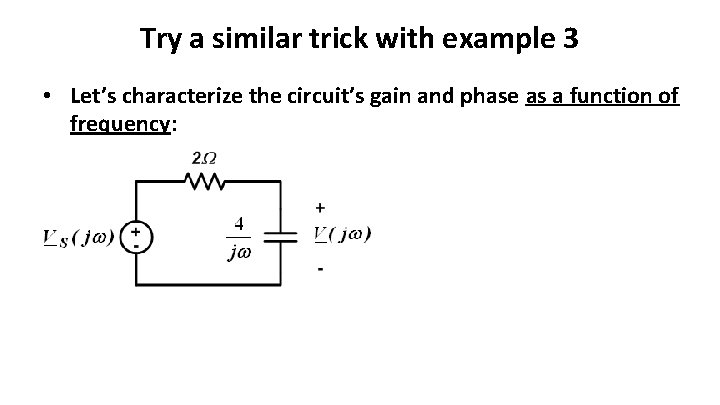
Try a similar trick with example 3 • Let’s characterize the circuit’s gain and phase as a function of frequency:

Example 3 – continued • Now we can use our trick to determine the circuit’s response to both inputs and superimpose the results v. S 1(t) = 3 cos(2 t+30 ) v. S 2(t) = 5 cos(4 t+60 )

• On the previous slide, write H, U, and Y as functions of frequency: – H(j 2), U(j 2), Y(j 2) – H(j 4), U(j 4), Y(j 4) • Note that we analyzed the circuit only once!

Super-important result • The steady-state sinusoidal response of a circuit is characterized by the frequency response, H(j ) • Magnitude response: output-to-input amplitude ratio vs. frequency • Phase response: difference between the output and input phases as a function of frequency

Frequency Response • In the time domain, we characterize systems by the differential equation relating the input and output • In the frequency domain, we characterize systems by their frequency response • Magnitude response and phase response give the gain and phase difference relating the input and output • The frequency of the signal (rather than time) is now our independent variable