Lecture 27 1 Interference Fringes For D d

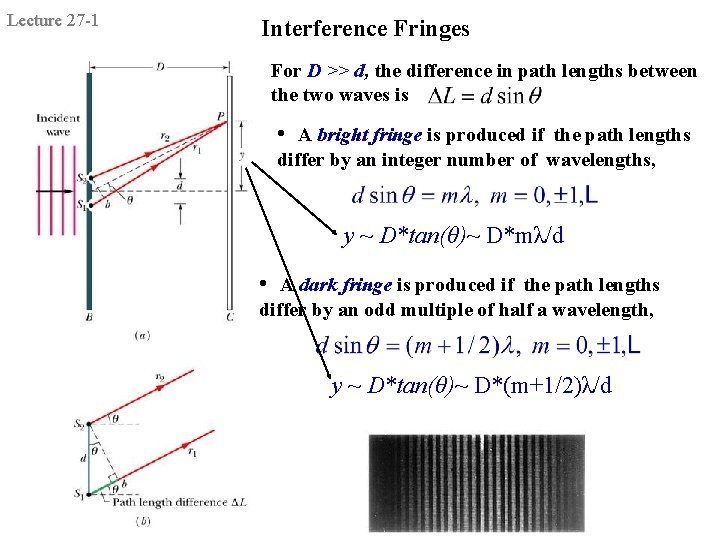
Lecture 27 -1 Interference Fringes For D >> d, the difference in path lengths between the two waves is • A bright fringe is produced if the path lengths differ by an integer number of wavelengths, y ~ D*tan(θ)~ D*mλ/d • A dark fringe is produced if the path lengths differ by an odd multiple of half a wavelength, y ~ D*tan(θ)~ D*(m+1/2)λ/d

Lecture 27 -2 Quiz Question 1 When the slits in Young’s experiment are moved closer together, the fringes A. remains unchanged. B. move closer together. C. move further apart.

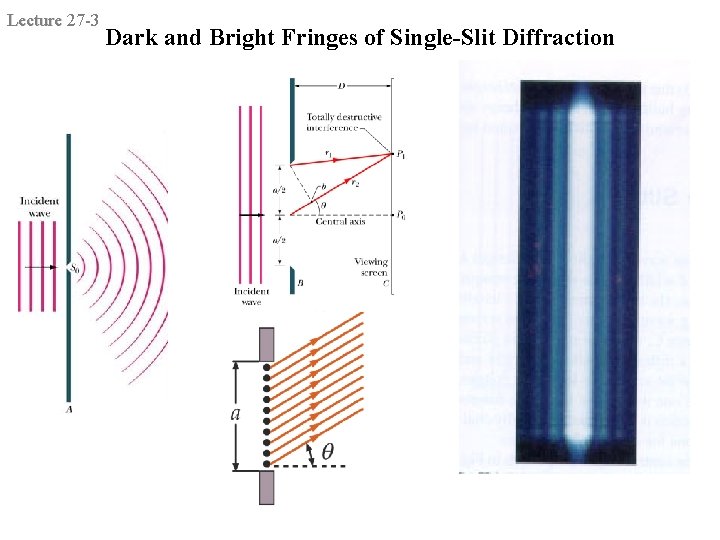
Lecture 27 -3 Dark and Bright Fringes of Single-Slit Diffraction

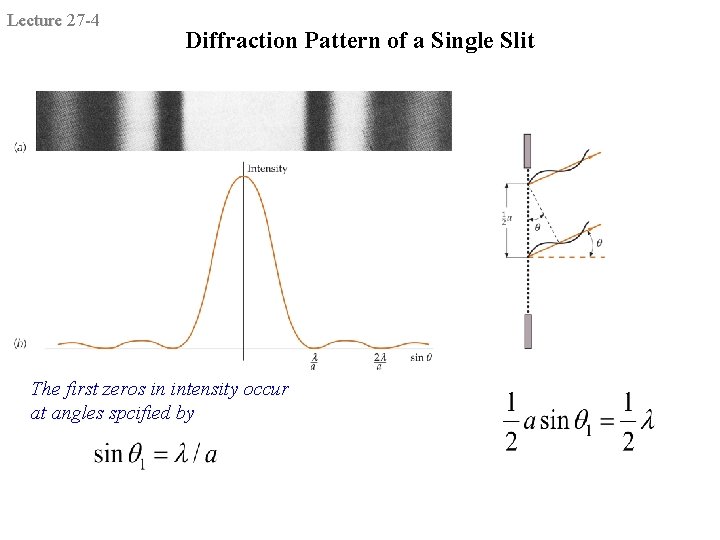
Lecture 27 -4 Diffraction Pattern of a Single Slit The first zeros in intensity occur at angles spcified by

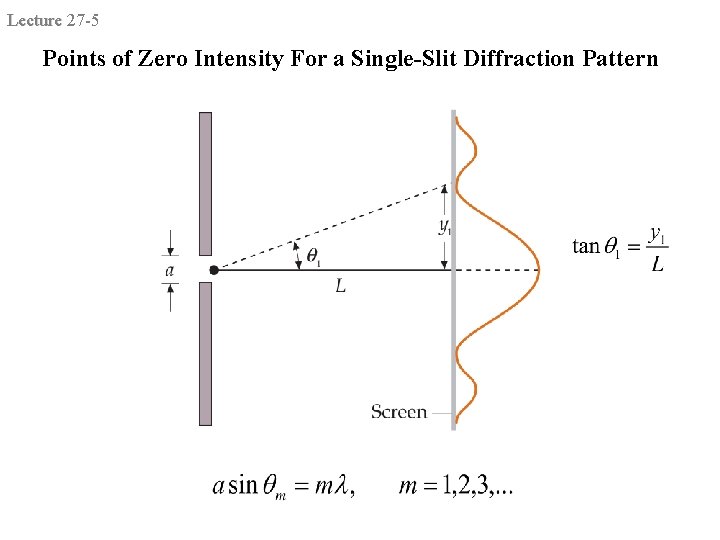
Lecture 27 -5 Points of Zero Intensity For a Single-Slit Diffraction Pattern

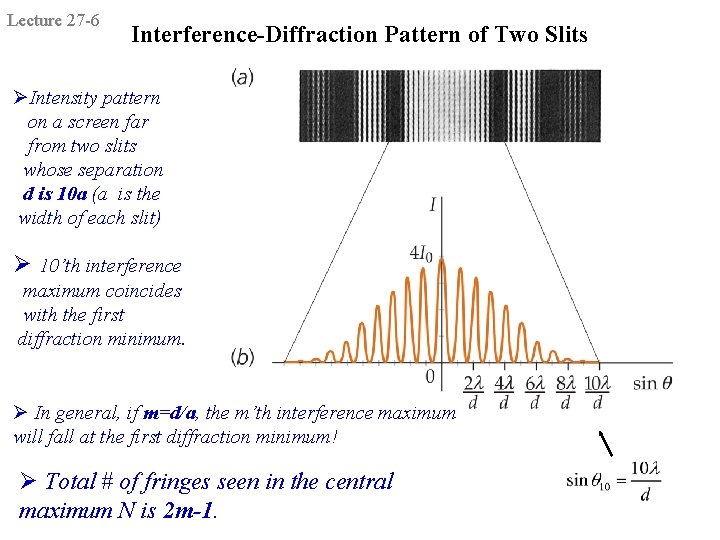
Lecture 27 -6 Interference-Diffraction Pattern of Two Slits ØIntensity pattern on a screen far from two slits whose separation d is 10 a (a is the width of each slit) Ø 10’th interference maximum coincides with the first diffraction minimum. Ø In general, if m=d/a, the m’th interference maximum will fall at the first diffraction minimum! Ø Total # of fringes seen in the central maximum N is 2 m-1.

Lecture 27 -7 Quiz Question 2 Two slits each with a width a=. 04 mm are separated by a distance d=. 16 mm and are illuminated by light of wavelength =400 nm. How many bright fringes are seen in the central diffraction maximum? A) 5 B) 7 C) 9 D) 11 E) None of above

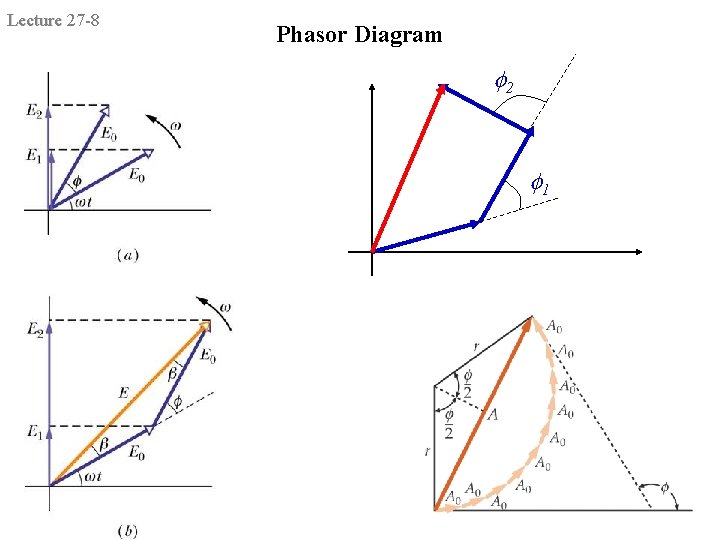
Lecture 27 -8 Phasor Diagram f 2 f 1

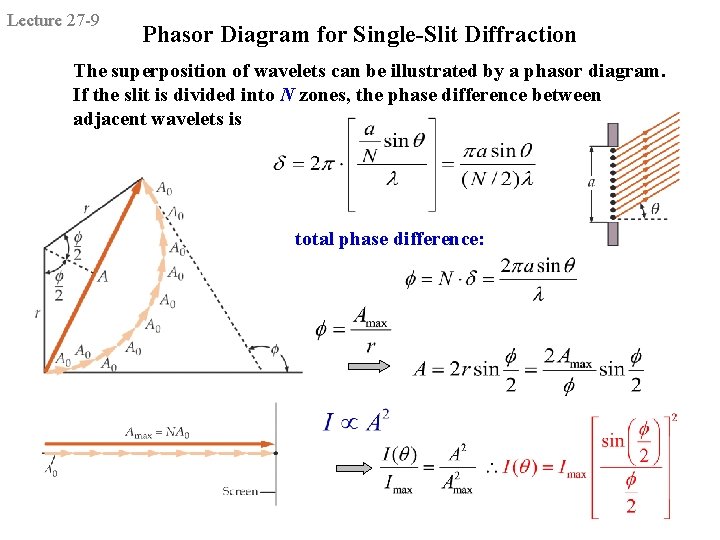
Lecture 27 -9 Phasor Diagram for Single-Slit Diffraction The superposition of wavelets can be illustrated by a phasor diagram. If the slit is divided into N zones, the phase difference between adjacent wavelets is total phase difference:

Lecture 27 -10 Young’s Double-Slit Experiment Revisited Intensity in terms of phase difference: a Intensity of each slit (I 0) is replaced by the diffraction pattern intensity due to each slit, I: The intensity for two slit interference-diffraction pattern is

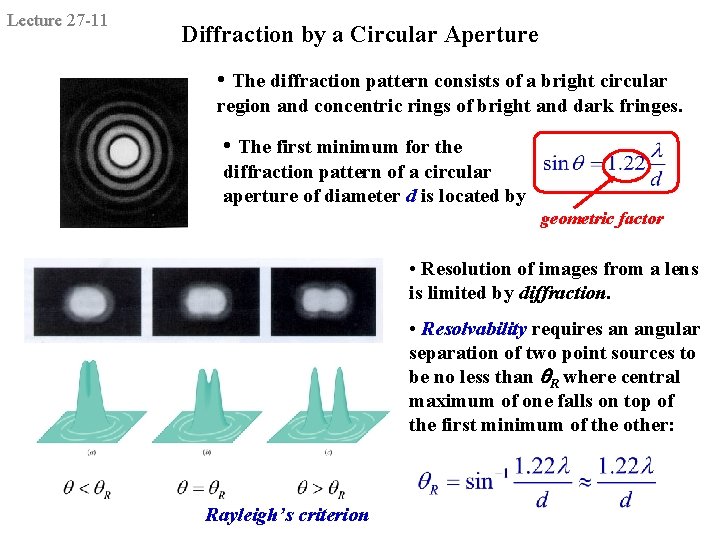
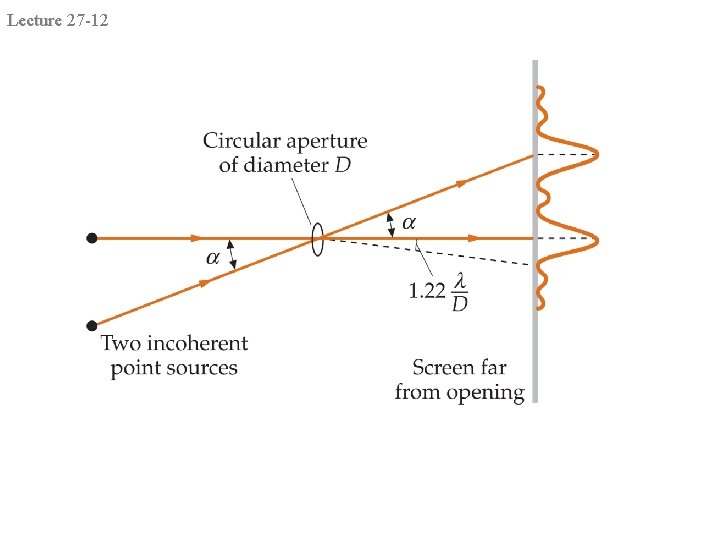
Lecture 27 -11 Diffraction by a Circular Aperture • The diffraction pattern consists of a bright circular region and concentric rings of bright and dark fringes. • The first minimum for the diffraction pattern of a circular aperture of diameter d is located by geometric factor • Resolution of images from a lens is limited by diffraction. • Resolvability requires an angular separation of two point sources to be no less than R where central maximum of one falls on top of the first minimum of the other: Rayleigh’s criterion

Lecture 27 -12

Lecture 27 -13 Diffraction Gratings • Devices that have a great number of slits or rulings to produce an interference pattern with narrow fringes. • One of the most useful optical tools. Used to analyze wavelengths. D Types of gratings: • transmission gratings • reflection gratings up to thousands per mm of rulings Maxima are produced when every pair of adjacent wavelets interfere constructively, i. e. , mth order maximum