LECTURE 25 SIMULATION AND MODELING CSE 411 Md

LECTURE 25 SIMULATION AND MODELING CSE 411 Md. Tanvir Al Amin, Lecturer, Dept. of CSE, BUET

Recap : Inverse Transform Method Find cumulative distribution function Let it be F Find F-1 X = F-1(R) is the desired variate where R ~ U(0, 1) Other methods are Accept Reject technique Composition method Convolution technique Special observations

Random variate for Continuous Distribution We already covered for continuous case : Proof of inverse transform method(Kelton 8. 2. 1 pg 440) Exponential distribution (Banks 8. 1. 1) Uniform distribution (Banks 8. 1. 2) Weibull distibution (Banks 8. 1. 3) Triangular distribution (Banks 8. 1. 4) Empirical continuous distribution (Banks 8. 1. 5) Continuous distributions without a closed form inverse (Self study – Banks 8. 1. 6)

Inverse Transform method for Discrete Distributions Banks Chapter 8. 1. 7 + Kelton 8. 2. 1

Things to remember If R ~ U(0, 1), A Random variable X will assume value x whenever, Also we should know the identities : We could use this identity also, It results in F-1(R) = floor(x) which is not useful because x is already an integer for discrete distribution.

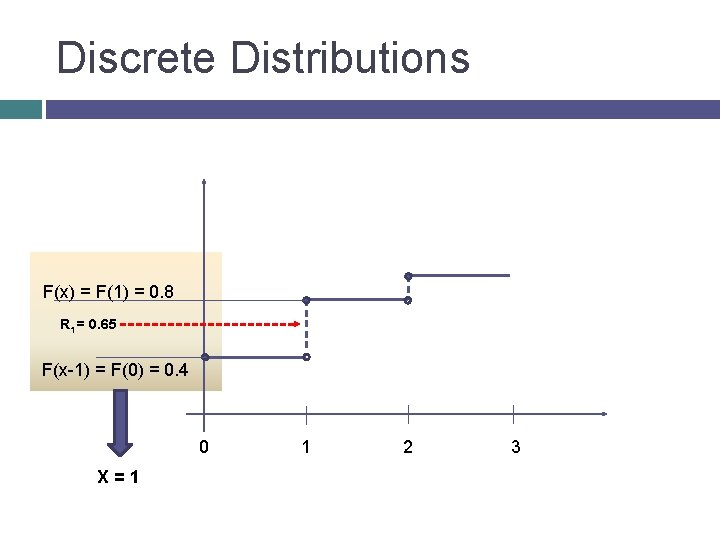
Discrete Distributions F(x) = F(1) = 0. 8 R 1 = 0. 65 F(x-1) = F(0) = 0. 4 0 X=1 1 2 3

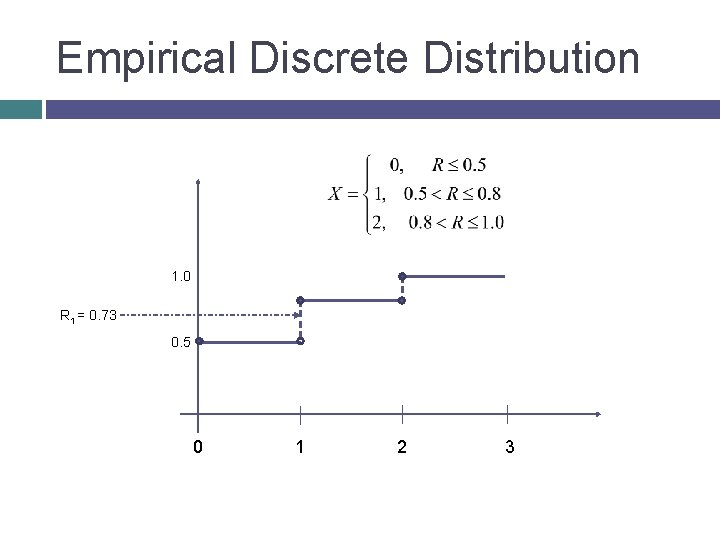
Empirical Discrete Distribution Say we want to find random variate for the following discrete distribution. At first find the F x p(x) 0 0. 50 1 0. 30 2 0. 20 x p(x) F(x) 0 0. 50 1 0. 30 0. 80 2 0. 20 1. 00

Empirical Discrete Distribution 1. 0 R 1 = 0. 73 0. 5 0 1 2 3

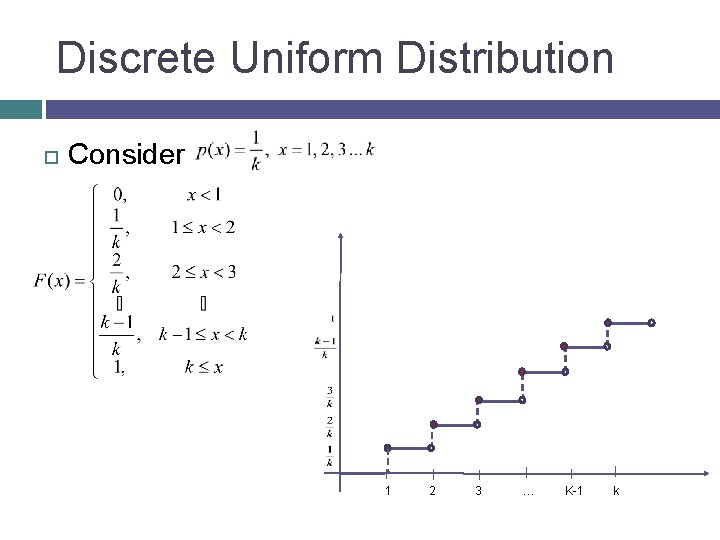
Discrete Uniform Distribution Consider 1 2 3 … K-1 k

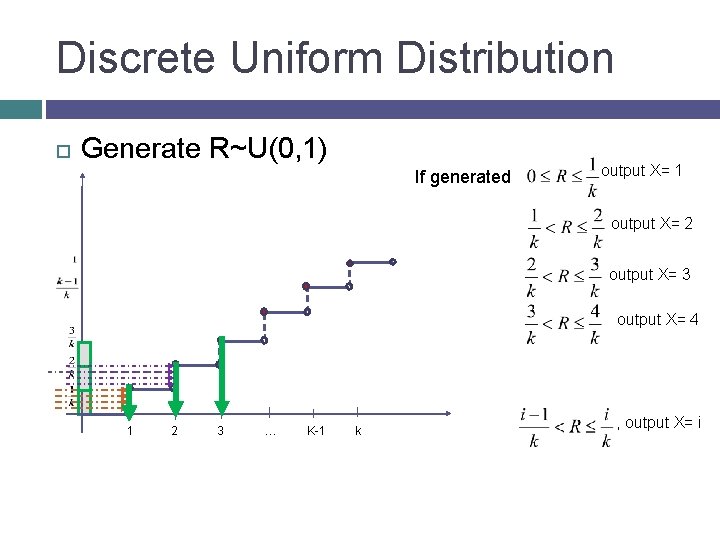
Discrete Uniform Distribution Generate R~U(0, 1) If generated output X= 1 output X= 2 output X= 3 output X= 4 1 2 3 … K-1 k , output X= i

Discrete Uniform Distribution , If generated output X=1 , output X=2 , output X=3 , output 4 , output X = i Imp : Expand this method for a general discrete uniform distribution DU(a, b)

Discrete Uniform Distribution Algorithm to generate random variate for p(x)=1/k where x = 1, 2, 3, … k Generate R~U(0, 1) uniform random number Return ceil(R*k)

Geometric Distribution Recall :

Geometric Distribution Algorithm to generate random variate for Generate R~U(0, 1) uniform random number Return ceil(ln(1 -R)/ln(1 -p)-1)

Proof of inverse transform method for Discrete case Kelton 8. 2. 1 Page 444 We need to show that

Disadvantage of Inverse Transform Method Kelton page 445 -448 Disadvantage Need to evaluate F-1. We may not have a closed form. In that case numerical methods necessary. Might be hard to find stopping conditions. For a given distribution, Inverse transform method may not be the fastest way

Advantage of Inverse Transform Method Straightforward method, easy to use Variance reduction techniques has an advantage if inverse transform method is used Facilitates generation of order statistics.

Composition Technique Kelton 8. 2. 2

Composition Technique Applies when the distribution function F from which we wish to generate can be expressed as a convex combination of other distributions F 1, F 2, F 3, … i. e. , for all x, F(x) can be written as

Composition Algorithm To generate random variate for Step 1 : Generate a positive random integer j such that Step 2 : Return X with distribution function Fj

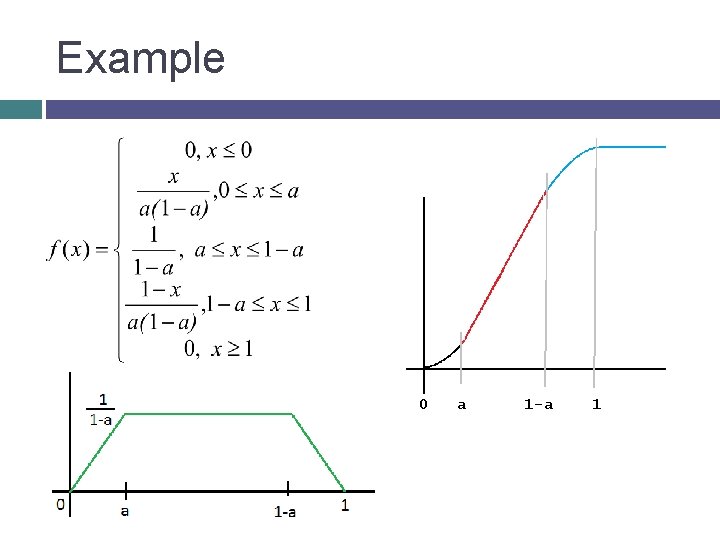
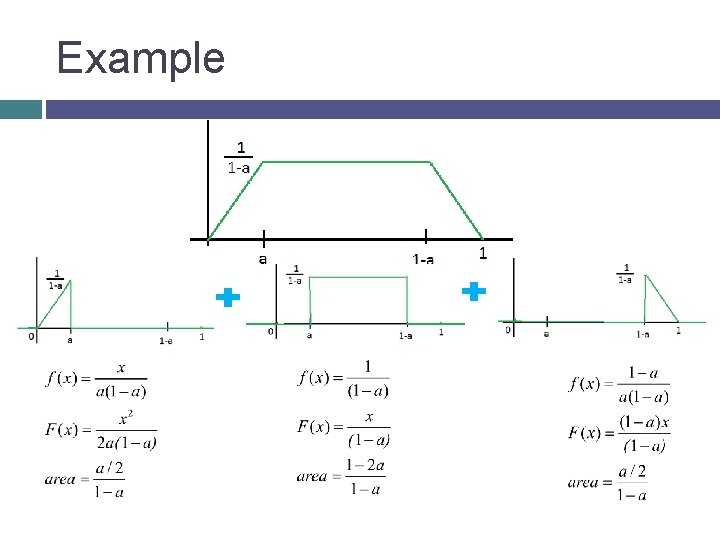
Geometric Interpretation For a continuous random variable X with density f, we might be able to divide the area under f into regions of areas p 1, p 2, …(corresponding to the decomposition of f into its convex combination representation) Then we can think of step 1 as choosing a region Step 2 as generating from the distribution corresponding to the chosen region

Example 0 a 1 -a 1

Example

Proof of composition technique Kelton page 449