Lecture 25 Introduction to steady state sinusoidal analysis

Lecture 25 • Introduction to steady state sinusoidal analysis • Overall idea • Qualitative example and demonstration • System response to complex inputs • Complex arithmetic review • Phasor representation of sinusoids • Related educational materials: –Chapter 10. 1 - 10. 3

Steady state sinusoidal response – overview • We have examined the natural response and step response of electrical circuits • We now consider the forced response of a circuit to sinusoidal inputs • We will only consider the steady state response to the sinusoidal input • Apply a sinusoidal input and let t • The steady state sinusoidal response • Corresponds to the particular solution

Why is this important? 1. Sinusoidal signals are very common • Power signals commonly sinusoidal (AC signals) • Carrier signals in communications often sinusoidal 2. The mathematics is considerably simpler • Differential equations become algebraic 3. System behavior often specified in terms of the system’s steady-state sinusoidal response • Example: Audio system specifications 4. It’s “natural” – our senses often work this way

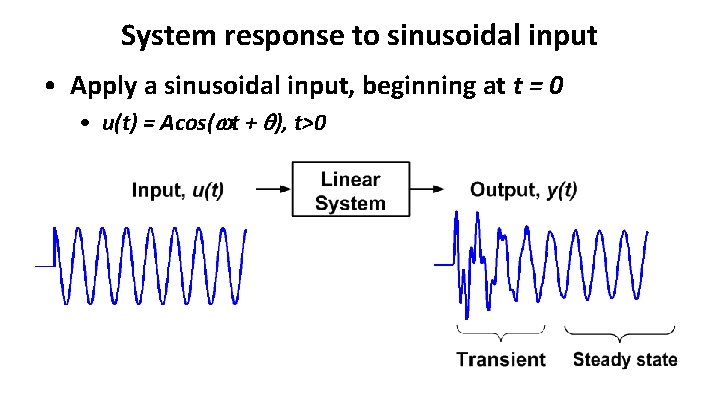
System response to sinusoidal input • Apply a sinusoidal input, beginning at t = 0 • u(t) = Acos( t + ), t>0

Sinusoidal response of linear systems • The steady state response of a linear system, to a sinusoidal input, will be a sinusoid of the same frequency (particular solution of same form as input) • The amplitude and phase can change • These changes are, in general, a function of the frequency

• Demo system response – Sinusoidal input to tower – Indicate response: transient, steady-state, frequency dependence

RL circuit steady state sinusoidal response • Apply a sinusoidal input to RL circuit: u(t) = Acos( t + ) • Governing equation (t ):

• Note on previous slide that di/dt is NOT zero for steady-state sinusoidal response!

Determining steady state sinusoidal responses • Obtaining solutions in terms of sines and cosines is tedious! • Try a “trick” involving complex exponentials: Acos( t + ) = Re{Aej( t+ )} = Re{Aej ej t} • Look at the response of the system to a complex exponential input, Aej ej t • Results in a complex exponential response, Bej ej t • The actual input is the real part of the complex input • The actual output is the real part of the complex output

• Note: Complex exponentials previously discussed in lecture 21. – We’ll do a little review, but it may be worthwhile for you to review lecture 21, if you are insecure about complex exponentials – we’ll be using them a LOT now • Point out that complex input not physically realizable!

RL circuit response – revisited • Apply a complex exponential input: u(t) = Aej ej t • Governing equation (t ) • Assume form of solution:

• Annotate last bullet of previous slide, to show di/dt and where terms go in governing differential equation

RL circuit response to complex input • Substitute assumed solution into governing equation: • We cancel ej t : • Since [Lej +R] is simply a complex number:

• Note in previous slide: – In equation 1, we no longer have a differential equation – it’s algebraic! – In equation 2, the governing equation is no longer even a function of time! (The coefficients are, however, functions of frequency) • The drawback: complex numbers are now involved. (Point out in equation 2) – We will do a little complex arithmetic review in the next few slides.

Complex numbers – review • Rectangular coordinates: • Polar coordinates: • Relationships:

Review of complex arithmetic • Given two complex numbers: • Addition: • Subtraction:

Review of complex arithmetic – continued • Multiplication: • Same two complex numbers: • Division:

Review of complex arithmetic • Multiplication: • Same two complex numbers, but in polar form: • Division:

• Annotate first “division” equation to note that 1/exp(phi) = exp(-phi)

Complex arithmetic – summary • Addition, subtraction generally easiest in rectangular coordinates • Add or subtract real and imaginary parts individually • Multiplication, division generally easiest in polar coordinates • Multiplication: multiply magnitudes, add phases • Division: divide magnitudes, subtract phases

Phasors • Recall: • Complex exponentials can be used to represent sinusoids • Complex exponentials can be written as a complex number multiplying a time-varying complex exponential • The complex number Aej provides the magnitude and phase of the original sinusoidal signal

Phasors – definition • The complex number (in polar form) providing the magnitude and phase of a sinusoidal signal is called a phasor.

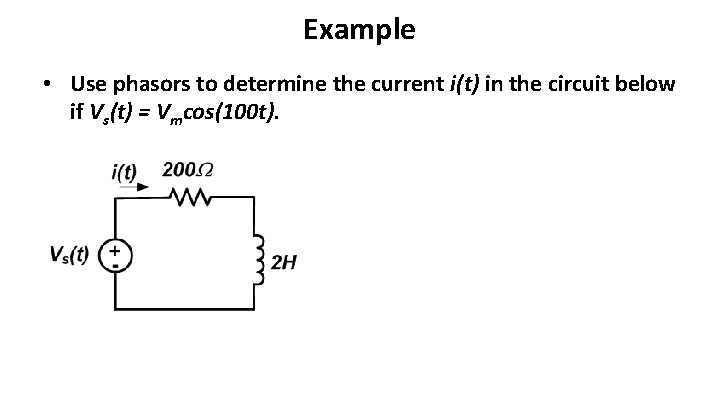
Example • Use phasors to determine the current i(t) in the circuit below if Vs(t) = Vmcos(100 t).

• In previous slide, show: – Change of input to complex exponential – Derivation of governing differential equation.

Example – continued • The governing differential equation is: • Since the input has the form , where is a phasor representing the input magnitude and phase, the output must be of the form , where is a phasor representing the output magnitude and phase.

• In previous slide, emphasize concepts. Do substitution and write algebraic equation.

Example – still continued…

• In previous slide, do complex arithmetic to solve for current phasor; convert back to time domain.

Example – Time domain signals • Input: • Response: • The response lags the input by 45