Lecture 24 Shared Objects and Concurrent Programming This

Lecture #24 Shared Objects and Concurrent Programming This material is not available in the textbook. The online powerpoint presentations contain the text explanations given in class. 1

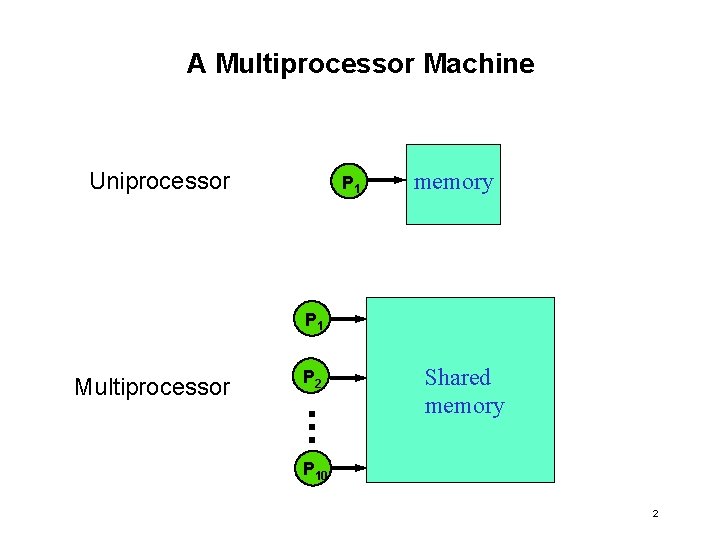
A Multiprocessor Machine Uniprocessor P 1 memory P 1 Multiprocessor . . P 2 Shared memory P 10 2

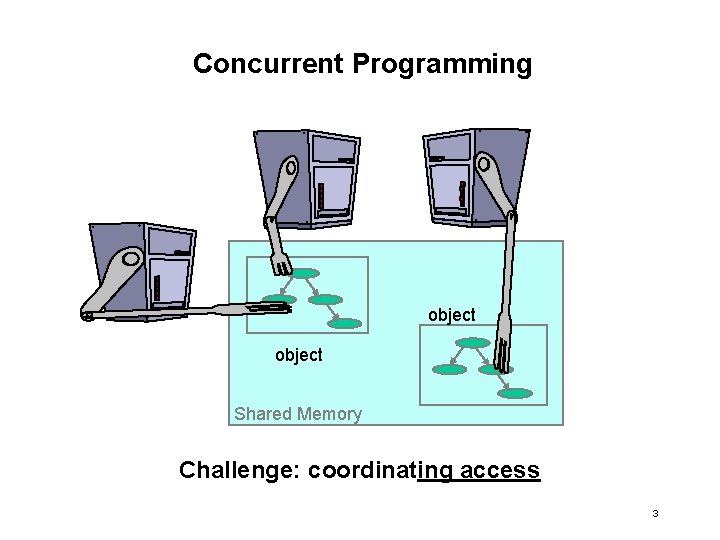
Concurrent Programming object Shared Memory Challenge: coordinating access 3

Persistent vs Transient Communication • Persistent Communication medium: the sending of information changes the state of the medium forever. Example: Blackboard. • Transient communication medium: the change of state is only for some limited time period. Example: Talking. 4

Parallel Primality Testing Task: Print all primes from 1 to 1010 in some order Avaliable: A machine with 10 processors Solution: Speed work up 10 times, that is, new time to print all primes will be 1/10 of time for single processor 5

Parallel Primality Testing 1 109 P 1 2 x 109 P 2 … … 1010 P 10 Split the work among processors! Each processor Pi gets 109 numbers to test. 6

Parallel Primality Testing (define (P i) (let ((counter (+ 1 (* (- i 1) (power 10 9)))) (upto (* i (power 10 9)))) (define (iter) (if (< counter upto) (begin (if (prime? counter) (display counter) #f) (increment-counter) (iter)) 'done)) (iter))) (parallel-execute (P 1) (P 2). . . (P 10)) 7

Problem: work is split unevenly Some processors have less primes to test… Some composite numbers are easier to test… 1 109 P 1 2 x 109 P 2 1010 P 10 Need to split the work range dynamically! 8

A Shared Counter Object (define (make-shared-counter value) (define (fetch) value) (define (increment) (set! value (+ 1 value)) (define (dispatch m) (cond (((eq? m 'fetch) (fetch)) (eq? m 'increment) (increment)) (else (error “unknown request”)))) dispatch) (define shared-counter (make-shared-counter 1)) 9

Using the Shared Counter (define (P i) (define (iter) (let ((index (shared-counter 'fetch))) (if (< index (power 10 10)) (begin (if (prime? index) (display index) #f) (shared-counter 'increment) (iter)) 'done)) (iter))) (parallel-execute (P 1) (P 2). . . (P 10)) 10

This Solution Doesn’t Work (let ((index (shared-counter 'fetch))) P 1 fetch 77 P 2 fetch 77 Error! 77 Increment: (set! value (+ 1 value)) time 77 P 1 read value 78 Error! 87 77 P 2 increment 10 times set! value 11

It Will Never Work!? Real World Example: Walking in the Street Look / Move Computers: Accessing Memory Fetch / Increment Fischer Lynch & Patterson: Impossible to solve!!! Need to “glue” the Fetch / Increment pair into one indivisible operation: Fetch-and-Increment 12

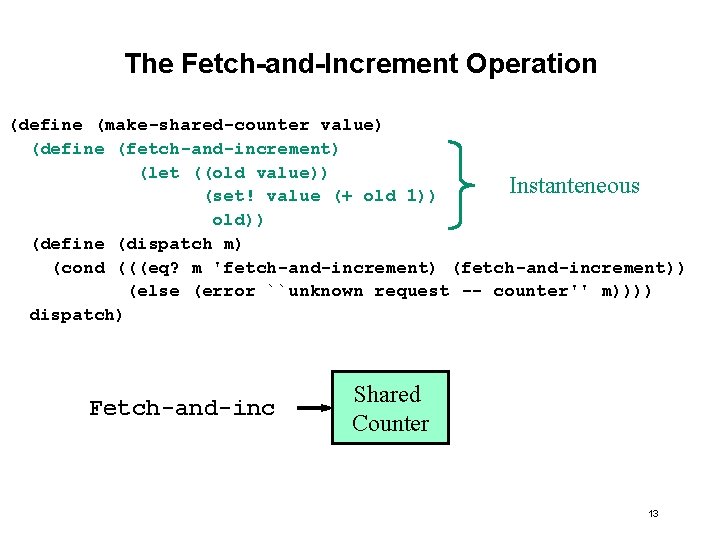
The Fetch-and-Increment Operation (define (make-shared-counter value) (define (fetch-and-increment) (let ((old value)) Instanteneous (set! value (+ old 1)) old)) (define (dispatch m) (cond (((eq? m 'fetch-and-increment) (fetch-and-increment)) (else (error ``unknown request -- counter'' m)))) dispatch) Fetch-and-inc Shared Counter 13

A Correct Shared Counter (define shared-counter (make-shared-counter 1)) (define (P i) (define (iter) (let ((index (shared-counter 'fetch-and-increment))) (if (< index (power 10 10)) (begin (if (prime? index) (display index) #f) (iter)) 'done)) (iter))) (parallel-execute (P 1) (P 2). . . (P 10)) 14

Implementing Fetch-and-Inc To make the program work we need an “intantaneous” implementation of fetch-and-increment. How can we do this: • Special Hardware. Built-in synchronization instructions. • Special Software. Use regular instructions -- the solution will involve waiting. Software: Mutual Exclusion 15

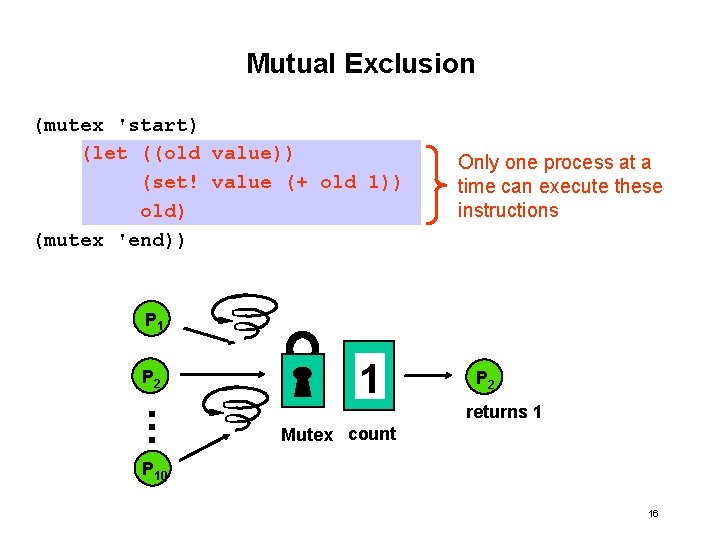
Mutual Exclusion (mutex 'start) (let ((old value)) (set! value (+ old 1)) old) (mutex 'end)) Only one process at a time can execute these instructions P 1 . . P 2 1 P 2 returns 1 Mutex count P 10 16

The Story of Alice and Bob Alice Bob Yard * As told by Leslie Lamport 17

The Mutual Exclusion Problem Requirements: • Mutual Exclusion: there will never be two dogs simultaneously in the yard. • No Deadlock: if only one dog wants to be in the yard it will succeed, and if both dogs want to go out, at least one of them will succeed. 18

Cell Phone Solution Alice Bob Yard 19

Coke Can Solution Alice Bob Yard 20

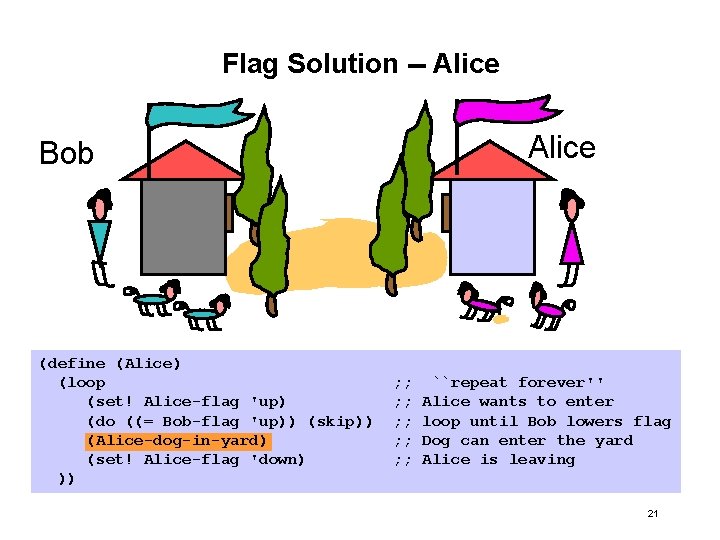
Flag Solution -- Alice Bob (define (Alice) (loop (set! Alice-flag 'up) (do ((= Bob-flag 'up)) (skip)) (Alice-dog-in-yard) (set! Alice-flag 'down) )) ; ; ; ; ; ``repeat forever'' Alice wants to enter loop until Bob lowers flag Dog can enter the yard Alice is leaving 21

Flag Solution -- Bob (define (Bob) (loop ; ; ``repeat forever'' (set! Bob-flag 'up) ; ; Bob wants to enter (do ((= Alice-flag 'up)) ; ; If Alice wants to enter (set! Bob-flag 'down) ; ; Bob is a gentleman (do ((= Alice-flag 'up)) (skip)) ; ; loop (skip) till Alice leaves (set! Bob-flag 'up) ; ; raise flag ) ; ; and go through the do again (Bob-dog-in-yard) ; ; Dog can enter yard (set! Bob-flag 'down) ; ; Bob is leaving )) 22

Flag Solution -- Both (define (Alice) (loop (set! Alice-flag 'up) (do ((= Bob-flag 'up)) (skip)) (Alice-dog-in-yard) (set! Alice-flag 'down) )) ; ; ; ; ; ``repeat forever'' Alice wants to enter loop until Bob lowers flag Dog can enter the yard Alice is leaving (define (Bob) (loop ; ; ``repeat forever'' (set! Bob-flag 'up) ; ; Bob wants to enter (do ((= Alice-flag 'up)) ; ; If Alice wants to enter (set! Bob-flag 'down) ; ; Bob is a gentleman (do ((= Alice-flag 'up)) (skip)) ; ; loop (skip) till Alice leaves (set! Bob-flag 'up) ; ; raise flag ) ; ; and go through the do again (Bob-dog-in-yard) ; ; Dog can enter yard (set! Bob-flag 'down) ; ; Bob is leaving )) 23

Intuition: Why Mutual Exclusion is Preserved Each perform: • First raise the flag, to signal interest. Then • look to see if the other one has raised the flag. One can claim that the following flag principle holds: since Alice and Bob each raise their own flag and then look at the others flag, the last one to start looking must notice that both flags are up. 24

Why is there no Deadlock? Since Alice has priority over Bob…if neither is entering the critical section, both are repeatedly trying, and Bob will give Alice priority. Unfortunately, the algorithm is not a fair one, and Bob's dogs might eventually grow very anxious : -) 25

The Morals of our Story • The Mutual Exclusion problem cannot be solved using transient communication. (I. e. Cell-phones. ) • The Mutual Exclusion problem cannot be solved using interrupts or interrupt bits (I. e. Cans) • The Mutual Exclusion problem can be solved with one bit registers (I. e. Flags), memory locations that can be read and written (set!-ed). We cheated a little: the arbiter problem… 26

The Solution and Conclusion (define (Alice) (loop (mutex 'begin) (Alice-dog-in-yard) (mutex 'end) )) ; ; critical section Question: then why not execute all the code of the parallel prime-printing algorithm in a critical section? 27

Answer: Amdahl’s Law Speedup Overall = Execution_time_Old / Execution_time_New = 1 1 - Fraction_Enhanced + Fraction_Enhanced Speedup_Enhanced If 40% of the execution time and can be sped-up by a factor of 10 by using 10 processors. Then Speedup Overall = 1/(0. 6 + (0. 4/10)) = 1/0. 64 = 1. 56 28

Length of Critical Sections We want Linear Speedup: 100 processors = 100 times faster By Amdahl's law that means that Fraction_Enhanced = 1 No Sequential Parts!!!!! For a speedup of only 99 times: 1 -Fraction_Enhacned= 0. 0001 In other words, we must try and make the parts that are sequential (the critical sections) as short as possible!!!!! 29

Summarizing it all To summarize it all, our world is asynchronous, and yet with a bit of luck we have ways of overcoming this asynchrony to create powerful concurrent algorithms. This was best summarized by the quote which some attribute to Tommy Lasorda: “Life is the synchronicity of chance” Good Luck on Your Final Exam! 30