Lecture 23 Functional Programming Languages and the Influence

Lecture 23 Functional Programming Languages and the Influence of Lambda Calculus COMS W 4115 Programming Languages & Translators Maria Ayako Taku mat 2185@columbia. edu COMS W 4115 - PLT Columbia University 1 April 24, 2013

Why Functional Programming? You may have heard that: Simple XOR program: (1) functional programs are let xor p = match p with (false, x) -> x | (true, x) -> not x; ; very succinct and elegant, but… (2) they take forever to write and understand COMS W 4115 - PLT Columbia University 2 April 24, 2013

Outline I. What is Functional Programming? II. Lambda Calculus' Influence on Functional Programming III. Benefits of Functional Programming IV. OCaml in Action: An Entire Interpreter in 3 slides COMS W 4115 - PLT Columbia University 3 April 24, 2013

What is Functional Programming? • A "programming paradigm" that focuses on the evaluation of functions • Programs are defined as recursive functions, where each takes a single input and outputs a single result. • Recall lambda calculus nests functions in this manner. Ex: (+ (* 1 2) (- 4 3)) let f = In OCaml: a + b; ; COMS W 4115 - PLT Columbia University let a = 1*2 in let b = 4 -3 in 4 April 24, 2013

What is Functional Programming? • One important trademark of Functional Programming: It avoids both changes in state and mutable data These expressions are not equal. //F# let a=42; //C# int a=42; Conceptually, they are more like this. //F# let a=42; //C# static int a(){ return 42; } http: //johnnycoder. com/blog/2009/04/20/functional-programming-part-1/ COMS W 4115 - PLT Columbia University 5 April 24, 2013

What is Functional Programming? Some Common (more or less) FP Languages: So what's the value in functional programming? • • • Are its benefits worth taking the time to learn it and overcoming the (possibly) steep learning curve? LISP OCaml Haskell Erlang F# (multi-paradigm) COMS W 4115 - PLT Columbia University 6 April 24, 2013

Outline I. What is Functional Programming? II. Lambda Calculus' Influence on Functional Programming III. Benefits of Functional Programming IV. OCaml in Action: An Entire Interpreter in 3 slides COMS W 4115 - PLT Columbia University 7 April 24, 2013

Lambda Calculus' Influence • The syntax and theory of Functional Programming is highly influenced by lambda calculus. • Knowledge of lambda calculus means that FP is easier to learn, understand, and use efficiently. You might recognize some of the following FP syntax traits from lambda calculus… COMS W 4115 - PLT Columbia University 8 April 24, 2013

Lambda Calculus' Influence Function Abstraction Lambda Calculus Recap A function abstraction consists of four parts: 1. 2. 3. 4. λx. expr a lambda followed by a single variable, a period, and then an expression COMS W 4115 - PLT Columbia University 9 April 24, 2013

Lambda Calculus' Influence Function Abstraction Lambda Calculus: OCaml: λx. expr fun x -> expr; ; Algebra: f(x) = expr COMS W 4115 - PLT Columbia University 10 April 24, 2013

Lambda Calculus' Influence Function Abstraction The Let Command • Named Functions: OCaml strays from pure functional programming at times. fun x -> expr; ; is equivalent to let my. Func x = expr; ; • The "let" command can be used to allow one to create named functions COMS W 4115 - PLT Columbia University 11 April 24, 2013

Lambda Calculus' Influence Function Abstraction An OCaml "let" example Similar code in Java COMS W 4115 - PLT Columbia University # let f. Toc temp = (temp -. 32. 0)/. 1. 8; ; # f. Toc 98. 6; ; - : float = 36. 9999 double f. Toc (double temp) { return (temp-32)/1. 8; } f. Toc(98. 6); 12 April 24, 2013

Lambda Calculus' Influence Beta Reductions Lambda Calculus Recap A function application is evaluated via a beta reduction Examples: (λx. xzx)y → [y/x]xzx = yzy (λx. + 1 x)7 → + 1 7 = 8 Which occurs when an actual value is substituted for a variable Layman's Terms: (λx. expr 1)expr 2 means "replace every instance of x in expr 1 with expr 2" COMS W 4115 - PLT Columbia University 13 April 24, 2013

Lambda Calculus' Influence Beta Reductions OCaml: Lambda Calculus: (fun x ->expr 1)expr 2; ; (λx. expr 1)expr 2 Example Usage: (fun x ->x*x)5; ; (* Evaluates to 5*5 = 25 *) COMS W 4115 - PLT Columbia University 14 April 24, 2013

Lambda Calculus' Influence Beta Reductions The Let Command (fun x ->expr 1)expr 2; ; The "let" command can once again be used to perform similar functionality to the "fun" command. COMS W 4115 - PLT Columbia University Is semantically equivalent to: let x = expr 2 in expr 1; ; Example Usage: let x = 5 in x*x; ; (* Evaluates to 5*5=25*) 15 April 24, 2013

Outline I. What is Functional Programming? II. Lambda Calculus' Influence on Functional Programming III. Benefits of Functional Programming IV. OCaml in Action: An Entire Interpreter in 3 slides COMS W 4115 - PLT Columbia University 16 April 24, 2013

Benefits of Functional Programming A few benefits in a nutshell: 1. Succinct Code 2. Encourages disciplined and logical thinking 3. Lazy Evaluation 4. Higher Level Functions Example: List. fold_left (fun s e ->s + e) 0 [42; 17; 120]; ; 5. No Side Effects & Referential Transparency COMS W 4115 - PLT Columbia University 17 April 24, 2013

Benefits of Functional Programming No Side Effects Side Effect: a function or expression has a side effect if it modifies state or has an observable interaction with the "outside world. " Examples: • Modify global/static variables • Modify arguments • Write data to a display or file Functional programs contain no assignment statements. So variables, once given a value, never change. COMS W 4115 - PLT Columbia University 18 April 24, 2013

Benefits of Functional Programming No Side Effects Simple Side Effect Example in Java static int x = 5; static void change. X (int a){ x = a; } change. X(4); // This function has the side effect // of changing the value of global var x COMS W 4115 - PLT Columbia University 19 April 24, 2013

Benefits of Functional Programming Referential Transparency: An expression (e. g. , function) is referentially transparent if it always produces the same output for the same input. Lack of side effects results in referential transparency. COMS W 4115 - PLT Columbia University Because of this behavior, a variable/expression can always be replaced with its value without changing the behavior of a program if that language has Referential Transparency. 20 April 24, 2013

Benefits of Functional Programming Referential Transparency Lack of Referential Transparency in Java static int x = 10; static int add(int a){ return a + x; } add(1); // returns 11 x = 0; add(1); // returns 10, even though same input. NOT RT! COMS W 4115 - PLT Columbia University 21 April 24, 2013

Why are Referential Transparency and Lack of Side Effects Good? • Elimination of bugs • Debugging in general is easier • Independence of evaluation order • Safe reuse of subprograms • Safe multithreading COMS W 4115 - PLT Columbia University 22 April 24, 2013

Why are Referential Transparency and Lack of Side Effects Good? Easier and Better Compiling Easier to Compile – It's not only people that benefit from being able to better predict and understand a program's behavior Better Compiling – optimization via: – Memoization – Parallelization – Common Subexpression Elimination COMS W 4115 - PLT Columbia University 23 April 24, 2013

Outline I. What is Functional Programming? II. Lambda Calculus' Influence on Functional Programming III. Benefits of Functional Programming IV. OCaml in Action: An Entire Interpreter in 3 slides COMS W 4115 - PLT Columbia University 24 April 24, 2013

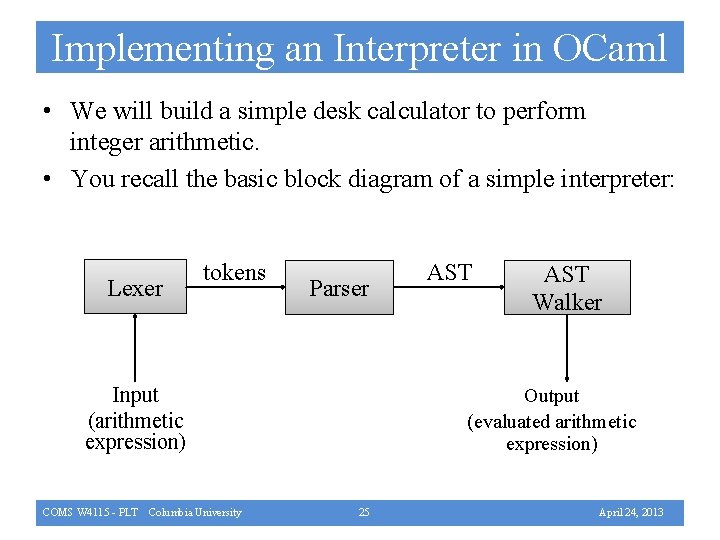
Implementing an Interpreter in OCaml • We will build a simple desk calculator to perform integer arithmetic. • You recall the basic block diagram of a simple interpreter: Lexer tokens Parser Input (arithmetic expression) COMS W 4115 - PLT Columbia University AST Walker Output (evaluated arithmetic expression) 25 April 24, 2013

Implementing an Interpreter in OCaml scanner. mll ast. mli { open Parser } rule token = parse [’ ’ ’t’ ’r’ ’n’] | ’+’ | ’-’ | ’*’ | ’/’ | [’ 0’-’ 9’]+ as lit | eof { token lexbuf } { PLUS } { MINUS } { TIMES } { DIVIDE } { LITERAL (int_of_string lit) } { EOF } type operator = Add | Sub | Mul | Div type expr = Binop of expr * operator * expr | Lit of int Courtesy of Stephen Edwards' PLT Lecture Slides: http: //www. cs. columbia. edu/~sedwards/classes/2012/w 4115 -fall/ocaml. pdf COMS W 4115 - PLT Columbia University 26 April 24, 2013

Implementing an Interpreter in OCaml parser. mly %{ open Ast %} %token PLUS MINUS TIMES DIVIDE EOF %token <int> LITERAL %left PLUS MINUS %left TIMES DIVIDE expr: expr PLUS expr | expr MINUS expr | expr TIMES expr | expr DIVIDE expr | LITERAL { Binop($1, Add, $3) } { Binop($1, Sub, $3) } { Binop($1, Mul, $3) } { Binop($1, Div, $3) } { Lit($1) } %start expr %type <Ast. expr> expr %% COMS W 4115 - PLT Columbia University 27 April 24, 2013

Implementing an Interpreter in OCaml AST Walker: calc. ml open Ast let rec eval = function Lit(x) -> x | Binop (e 1, op, e 2) -> let v 1 = eval e 1 and v 2 = eval e 2 in match op with Add -> v 1 + v 2 | Sub -> v 1 - v 2 | Mul ->v 1 * v 2 | Div -> v 1 / v 2 let _ = let lexbuf = Lexing. from_channel stdin in let expr = Parser. expr Scanner. token lexbuf in let result = eval expr in print_endline (string_of_int result) COMS W 4115 - PLT Columbia University 28 April 24, 2013

Quick Side Note: Pattern Matching in OCaml Pattern Matching a Parameter (function…) Pattern Matching a Value (match…with) function param 1 -> expr 1 | param 2 -> expr 2 | param 3 -> expr 3 match expr with param 1 -> expr 1 | param 2 -> expr 2 | param 3 -> expr 3 Main difference is how the pattern matcher receives its value to match COMS W 4115 - PLT Columbia University 29 April 24, 2013

Quick Side Note: Pattern Matching in OCaml If you recall the XOR program from the beginning of this lecture, you should now be able to understand how this works. Hint: Variables, such as "x" will match anything and are bound to a value when the pattern matches. let xor p = match p with (false, x) -> x | (true, x) -> not x; ; COMS W 4115 - PLT Columbia University 30 April 24, 2013

Compiling the Interpreter $ ocamllex scanner. mll # create scanner. ml 8 states, 267 transitions, table size 1116 bytes $ ocamlyacc parser. mly # create parser. ml and parser. mli $ ocamlc –c ast. mli # compile AST types $ ocamlc –c parser. mli # compile parser types $ ocamlc –c scanner. ml # compile the scanner $ ocamlc –c parser. ml # compile the parser $ ocamlc –c calc. ml # compile the interpreter $ ocamlc –o calc parser. cmo scanner. cmo calc. cmo $. /calc 2*3+4*5 26 $ COMS W 4115 - PLT Columbia University 31 April 24, 2013

So Why Functional Programming? It's hard to get to compile, but once it compiles, it works -Unknown PLT Student COMS W 4115 - PLT Columbia University 32 April 24, 2013

References • Edwards, Stephen. “An Introduction to Objective Caml. ” http: //www. cs. columbia. edu/~sedwards/classes/2012/w 4115 -fall/ocaml. pdf • Huges, John. “Why Functional Programming Matters. ” Research Topics in Functional Programming, Addison. Wesley, 1990: pp 17 -42 • “Advantages of Functional Programming. ” http: //c 2. com/cgi/wiki? Advantages. Of. Functional. Program ming COMS W 4115 - PLT Columbia University 33 April 24, 2013