Lecture 22 Kruskal and Dijkstra Algorithms 1 Recap

Recap Maximal Flow technique and shortest route technique are other two techniques of network

Kruskal’s algorithm for finding MST Step 1: Sort all edges into nondecreasing order. Step

Example: A cable company want to connect five villages to their network which currently

Example: (Kruskal Algorithm) We model the situation as a network, then the problem is

Example: (Kruskal Algorithm) B 5 C 3 4 6 8 List the edges in

Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the shortest edge

Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the next shortest

Example: (Kruskal Algorithm) B 5 C 3 4 6 8 All vertices have been

The details for constructing MST l How do we check if a cycle is

Time complexity l Time complexity: O(|E| log|E|) – – 15 Step 1: O(|E| log|E|)

Dijkstra Algorithm l l l 16 Works with directed and undirected graphs Works with

Walk-Through Initialize array 2 A 5 F 10 7 3 C 4 8 4

Example: Update unselected nodes 2 A 5 F 10 7 3 C 4 8

Example: Select minimum distance 2 A 5 F 10 7 3 C 4 8

Example: Select minimum distance 2 A 5 F 10 7 C 4 8 4

Order of Complexity l Analysis find. Min() takes O(V) time – outer loop iterates

Order of Complexity If the graph is sparse, i. e. , |E| = O(V)

Summary In Kruskal algoritm, MST is form by taking small value edge which are

In Next Lecture l 36 In next lecture, we will discuss about greedy algorithms

Slides: 36

Download presentation

Lecture 22. Kruskal and Dijkstra Algorithms 1

Recap Maximal Flow technique and shortest route technique are other two techniques of network model. l In Maximal Flow technique , maximum flow capacity of different problems is solved and in shortest route technique you have to solve the problems where you need to find distance. l Prim’s algorithm is also example graph or network and solve for making Minimal spanning tree with time complexity O(n 2) l 2

Kruskal’s algorithm for finding MST Step 1: Sort all edges into nondecreasing order. Step 2: Add the next smallest weight edge to the forest if it will not cause a cycle. Step 3: Stop if n-1 edges. Otherwise, go to Step 2. 3

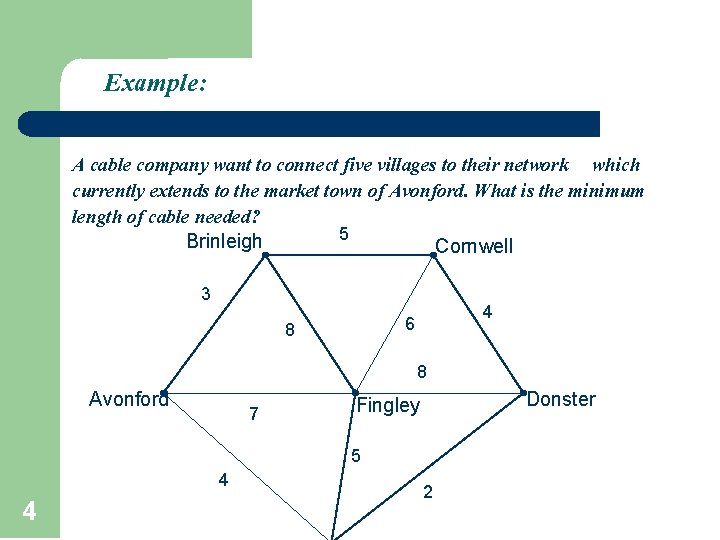
Example: A cable company want to connect five villages to their network which currently extends to the market town of Avonford. What is the minimum length of cable needed? 5 Brinleigh Cornwell 3 4 6 8 8 Avonford 7 Donster Fingley 5 4 4 2

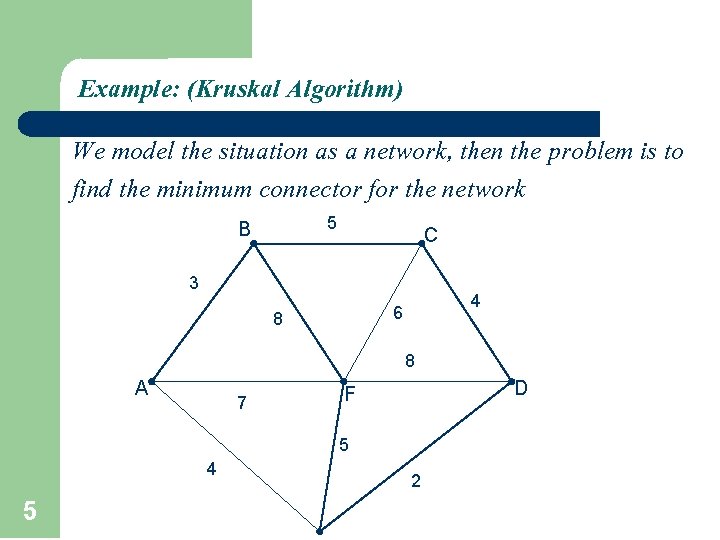
Example: (Kruskal Algorithm) We model the situation as a network, then the problem is to find the minimum connector for the network 5 B C 3 4 6 8 8 A 7 D F 5 4 5 2

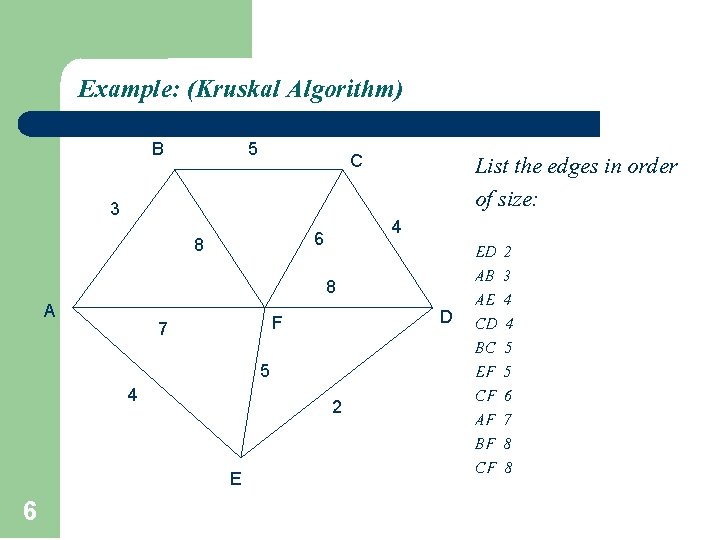
Example: (Kruskal Algorithm) B 5 C 3 4 6 8 List the edges in order of size: 8 A D F 7 5 4 2 E 6 ED 2 AB 3 AE 4 CD 4 BC 5 EF 5 CF 6 AF 7 BF 8 CF 8

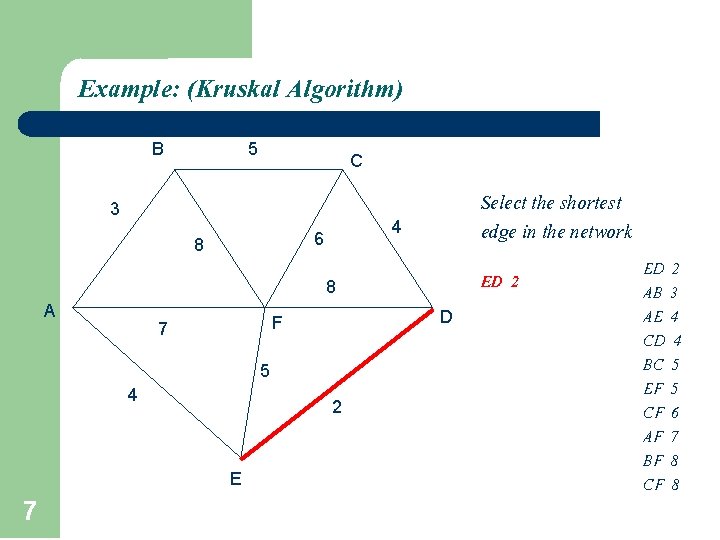
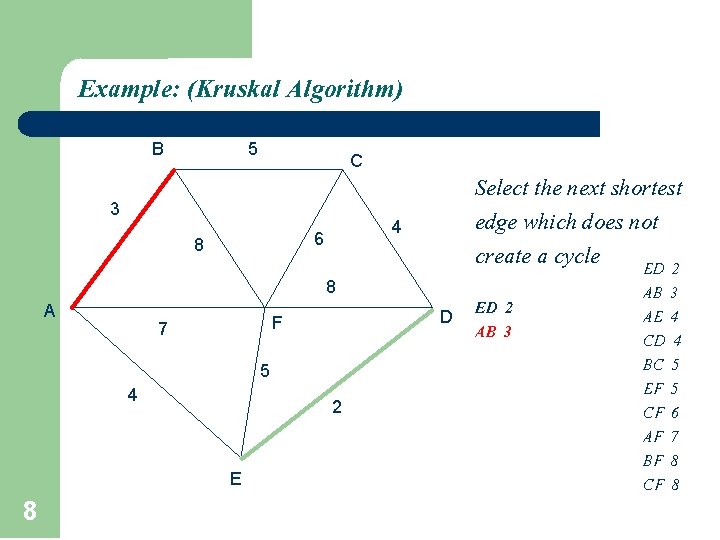
Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the shortest edge in the network ED 2 8 A D F 7 5 4 2 E 7 ED 2 AB 3 AE 4 CD 4 BC 5 EF 5 CF 6 AF 7 BF 8 CF 8

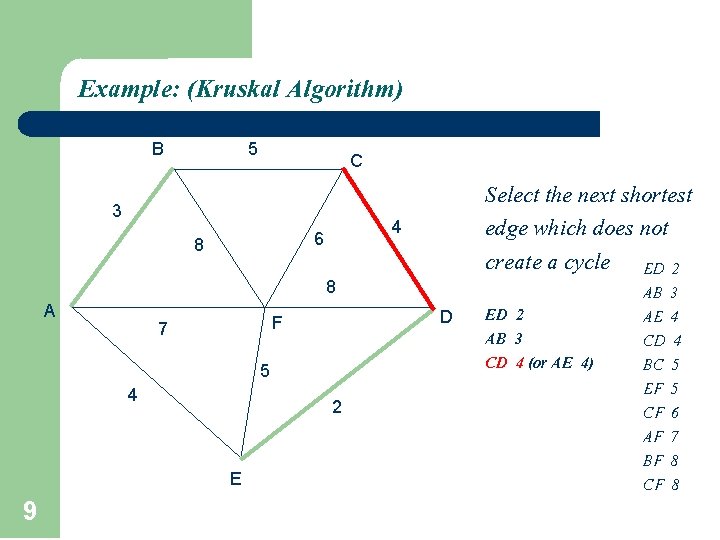
Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the next shortest edge which does not create a cycle ED 2 8 A D F 7 5 4 2 E 8 ED 2 AB 3 AE 4 CD 4 BC 5 EF 5 CF 6 AF 7 BF 8 CF 8

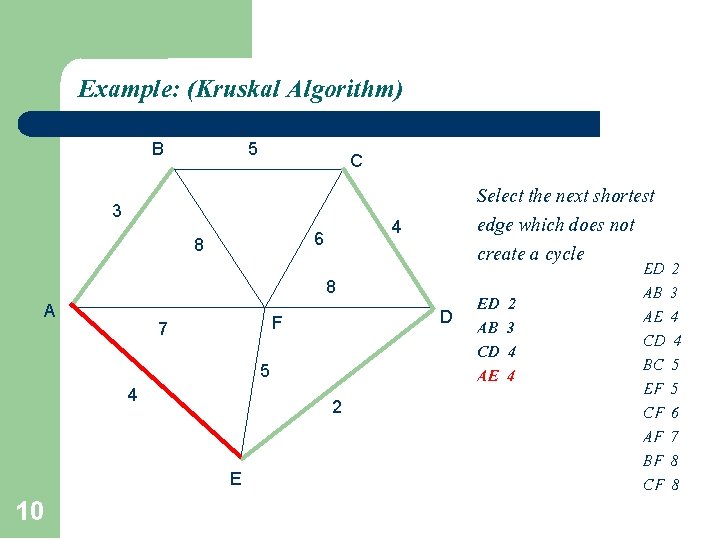
Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the next shortest edge which does not create a cycle ED 2 8 A D F 7 5 4 2 E 9 ED 2 AB 3 CD 4 (or AE 4) AB 3 AE 4 CD 4 BC 5 EF 5 CF 6 AF 7 BF 8 CF 8

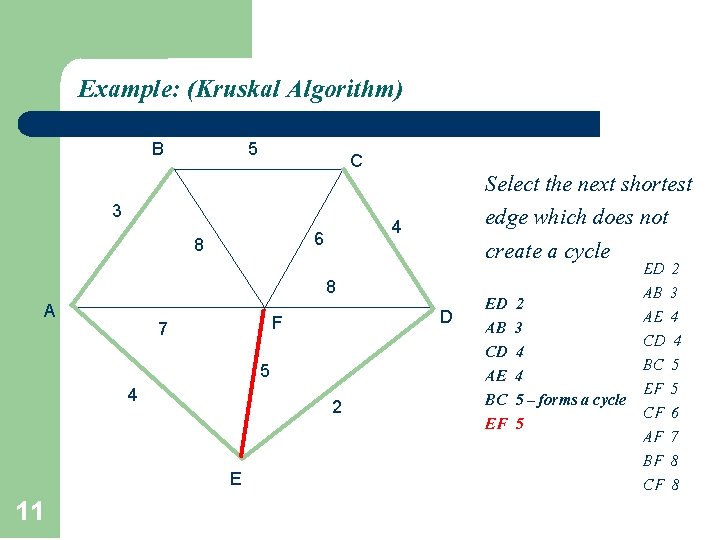
Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the next shortest edge which does not create a cycle 8 A D F 7 5 4 2 E 10 ED AB CD AE 2 3 4 4 ED 2 AB 3 AE 4 CD 4 BC 5 EF 5 CF 6 AF 7 BF 8 CF 8

Example: (Kruskal Algorithm) B 5 C 3 4 6 8 Select the next shortest edge which does not create a cycle 8 A D F 7 5 4 2 E 11 ED AB CD AE BC EF ED 2 AB 3 2 AE 4 3 CD 4 4 BC 5 4 EF 5 5 – forms a cycle CF 6 5 AF 7 BF 8 CF 8

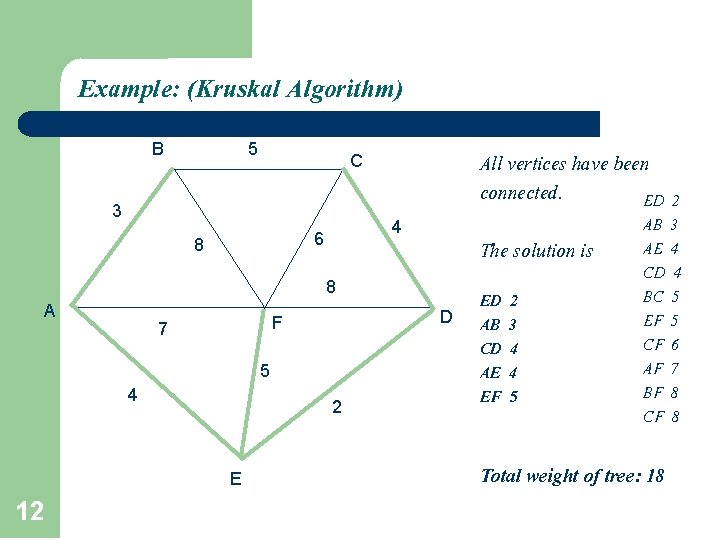
Example: (Kruskal Algorithm) B 5 C 3 4 6 8 All vertices have been connected. ED 2 The solution is 8 A D F 7 5 4 2 E 12 ED AB CD AE EF 2 3 4 4 5 AB 3 AE 4 CD 4 BC 5 EF 5 CF 6 AF 7 BF 8 CF 8 Total weight of tree: 18

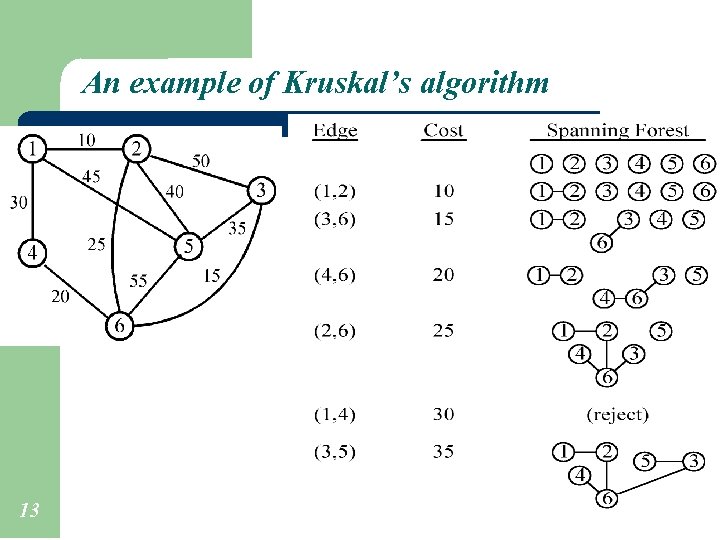
An example of Kruskal’s algorithm 13

The details for constructing MST l How do we check if a cycle is formed when a new edge is added? – l l l 14 By the SET and UNION method. A tree in the forest is used to represent a SET. If (u, v) E and u, v are in the same set, then the addition of (u, v) will form a cycle. If (u, v) E and u S 1 , v S 2 , then perform UNION of S 1 and S 2.

Time complexity l Time complexity: O(|E| log|E|) – – 15 Step 1: O(|E| log|E|) Step 2 & Step 3: Where is the inverse of Ackermann’s function.

Dijkstra Algorithm l l l 16 Works with directed and undirected graphs Works with weighted and unweighted graphs Rare type of algorithm A greedy algorithm that produces an optimal solution

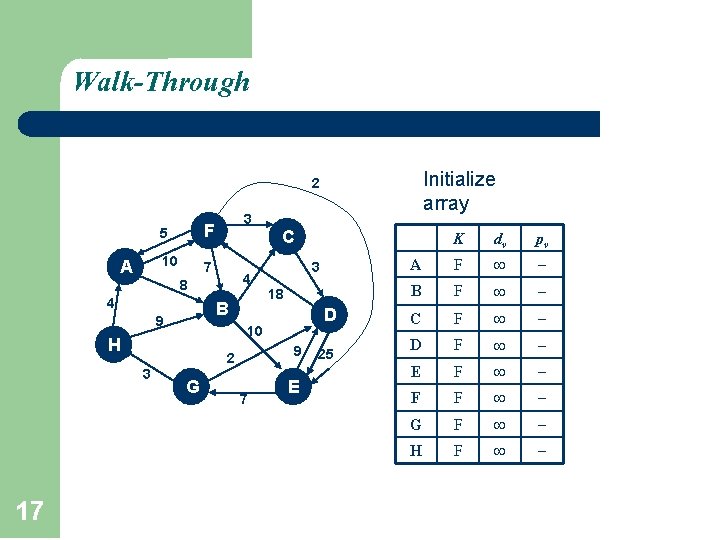
Walk-Through Initialize array 2 A 5 F 10 7 3 C 4 8 4 B 9 17 18 D 10 H 9 2 3 3 G 7 E 25 K dv pv A F B F C F D F E F F F G F H F

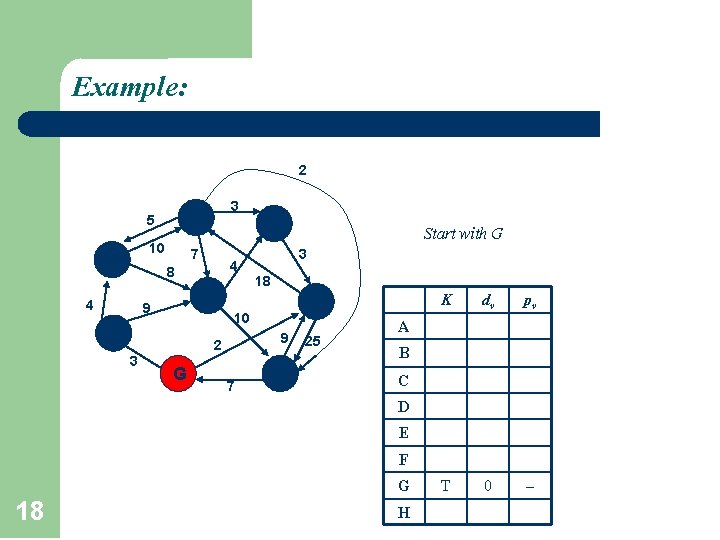
Example: 2 A 5 F 10 7 3 C 4 8 4 B 9 18 D 9 2 3 3 10 H G 7 Start with G E 25 K dv pv T 0 A B C D E F G 18 H

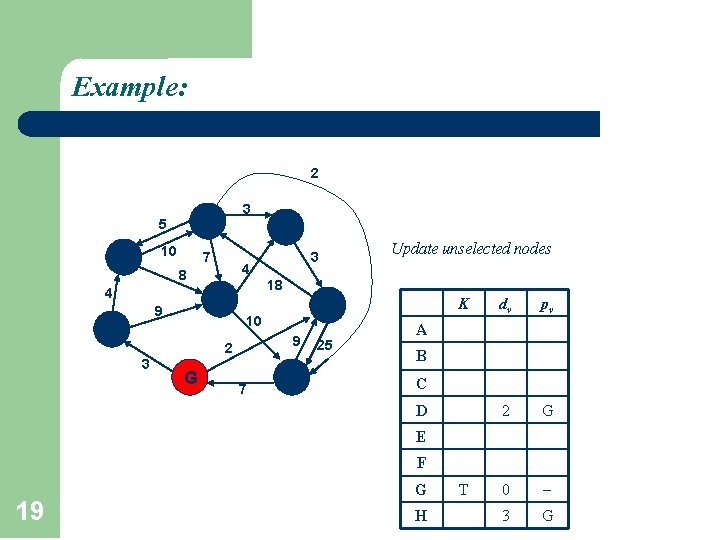
Example: 2 A 5 F 10 7 3 C 4 8 4 B 9 G 7 K D 9 2 3 18 10 H Update unselected nodes 3 E 25 dv pv 2 G 0 3 G A B C D E F 19 G H T

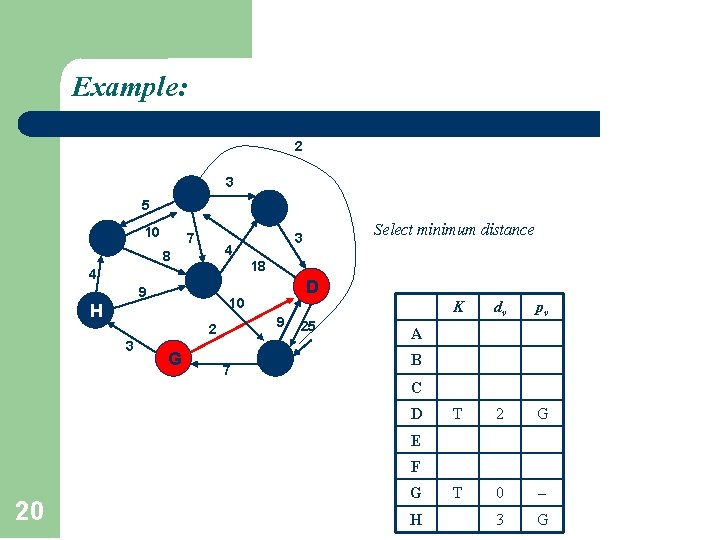
Example: 2 F 5 10 A 3 C 7 4 8 4 B 9 D 9 2 3 18 10 H G 7 Select minimum distance 3 E 25 K dv pv T 2 G T 0 3 G A B C D E F 20 G H

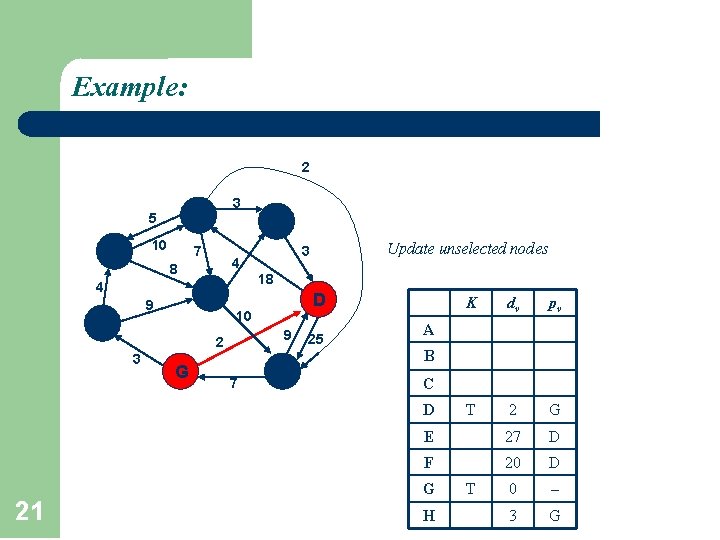
Example: 2 A 5 F 10 7 3 C 4 8 4 B 9 D 9 2 3 18 10 H G 7 Update unselected nodes 3 E 25 K dv pv T 2 G E 27 D F 20 D 0 3 G A B C D 21 G H T

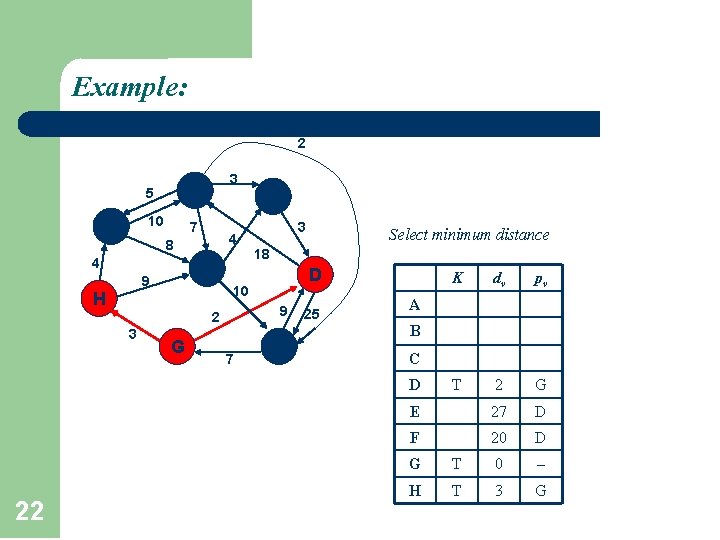
Example: 2 A 5 F 10 7 3 C 4 8 4 B 9 D 9 2 G 7 Select minimum distance 18 10 H 3 3 E 25 K dv pv T 2 G E 27 D F 20 D A B C D 22 G T 0 H T 3 G

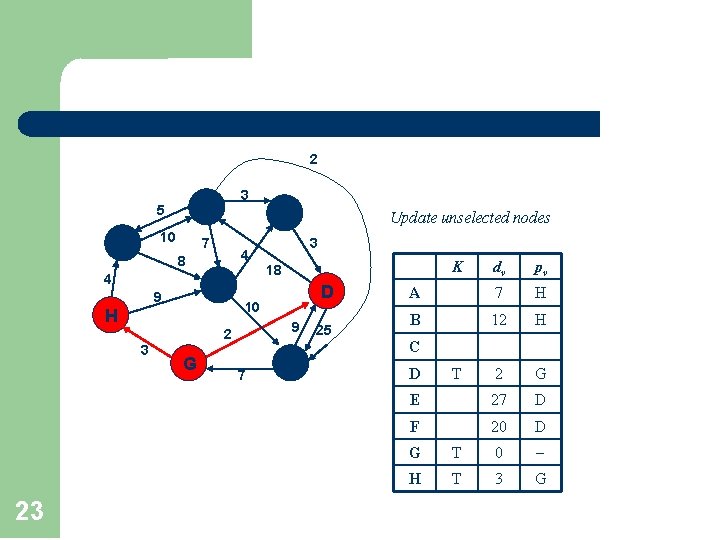
2 A 5 F 10 7 3 C 4 8 4 B 9 23 K G 7 dv pv A 7 H B 12 H 2 G E 27 D F 20 D 18 D 9 2 3 3 10 H Update unselected nodes E 25 C D T G T 0 H T 3 G

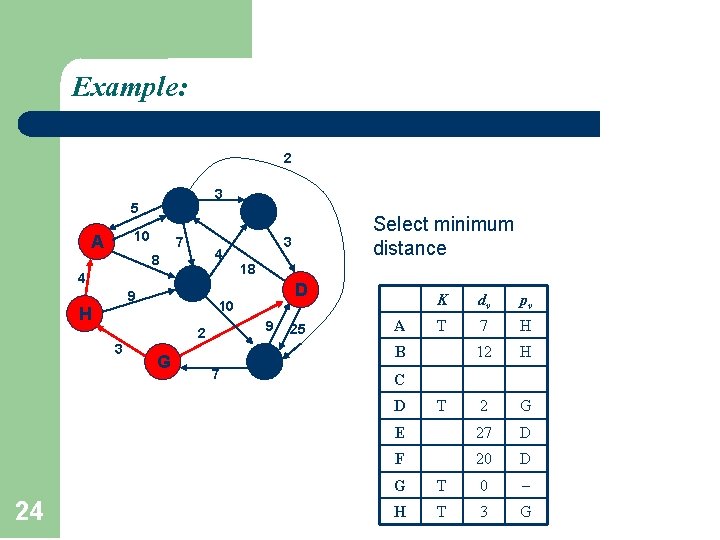
Example: 2 A 5 F 10 7 3 C 4 8 4 B 9 18 D 9 2 3 3 10 H G 7 Select minimum distance E 25 K dv pv T 7 H 12 H 2 G E 27 D F 20 D A B C D 24 T G T 0 H T 3 G

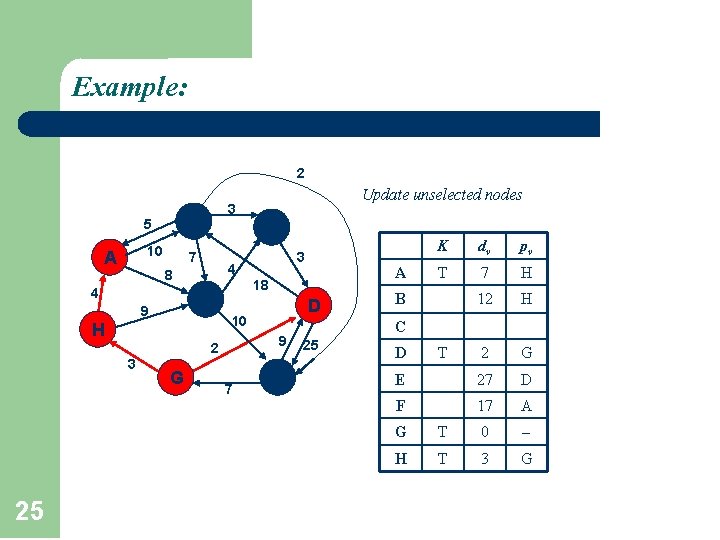
Example: 2 A 5 F 10 7 3 C 4 8 4 B 9 G 7 D E K dv pv T 7 H 12 H 2 G E 27 D F 17 A A 18 9 2 25 3 10 H 3 Update unselected nodes B C 25 D T G T 0 H T 3 G

Example: 2 A 5 F 10 7 3 4 8 4 B 9 G 7 K dv pv A T 7 H B T 12 H T 2 G E 27 D F 17 A 18 D 9 2 26 3 10 H 3 Select minimum distance C E 25 C D G T 0 H T 3 G

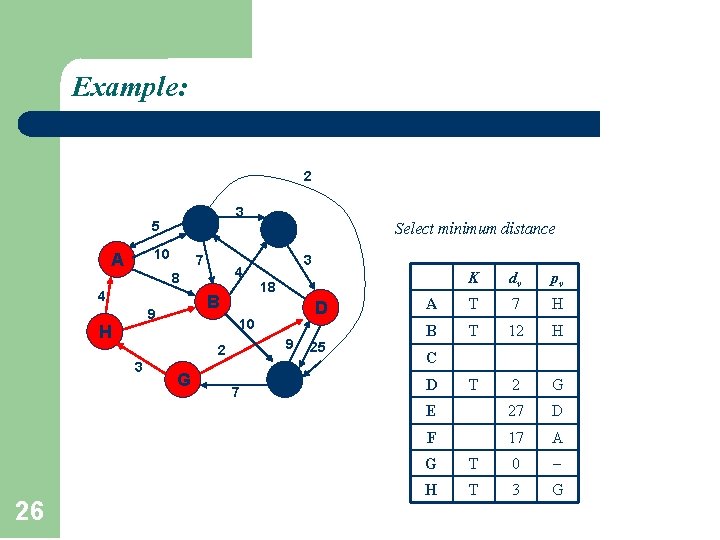
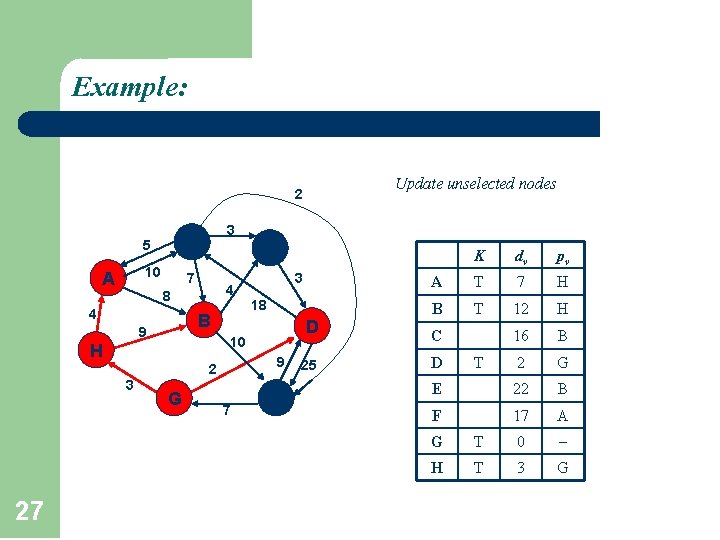
Example: Update unselected nodes 2 A 5 F 10 7 3 C 4 8 4 B 9 D 9 2 27 18 10 H 3 3 G 7 E 25 K dv pv A T 7 H B T 12 H 16 B 2 G E 22 B F 17 A C D T G T 0 H T 3 G

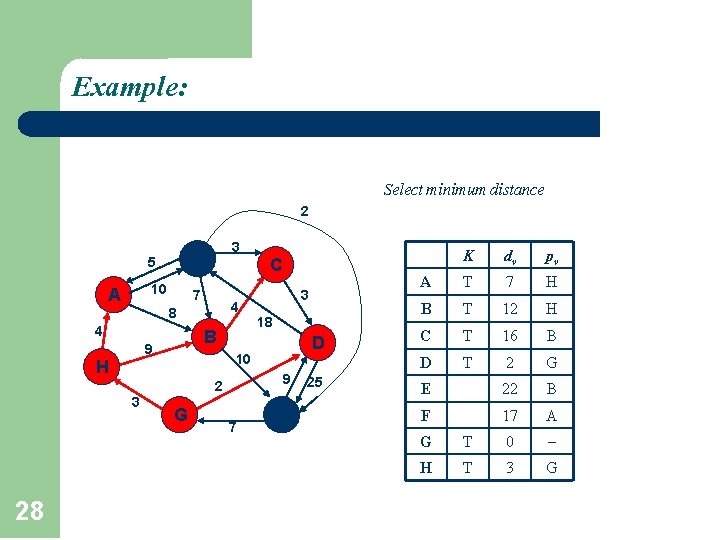
Example: Select minimum distance 2 A 5 F 10 7 3 C 4 8 4 B 9 D 9 2 28 18 10 H 3 3 G 7 E 25 K dv pv A T 7 H B T 12 H C T 16 B D T 2 G E 22 B F 17 A G T 0 H T 3 G

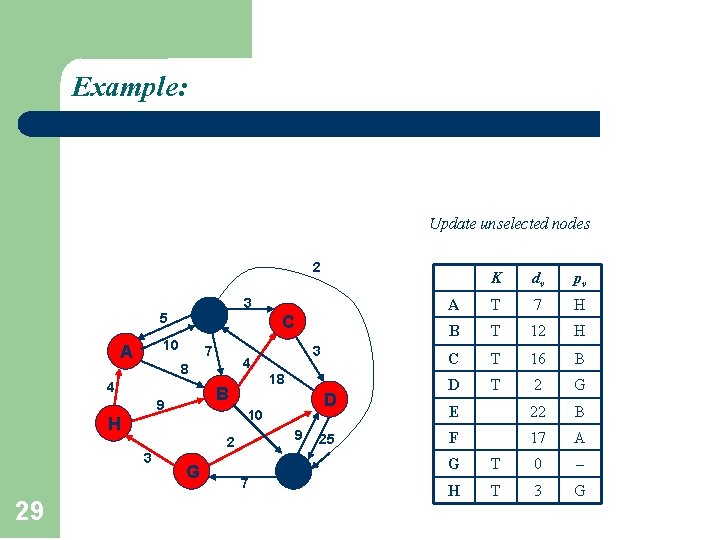
Example: Update unselected nodes 2 A 5 F 10 7 3 C 4 8 4 B 9 D 9 2 29 18 10 H 3 3 G 7 E 25 K dv pv A T 7 H B T 12 H C T 16 B D T 2 G E 22 B F 17 A G T 0 H T 3 G

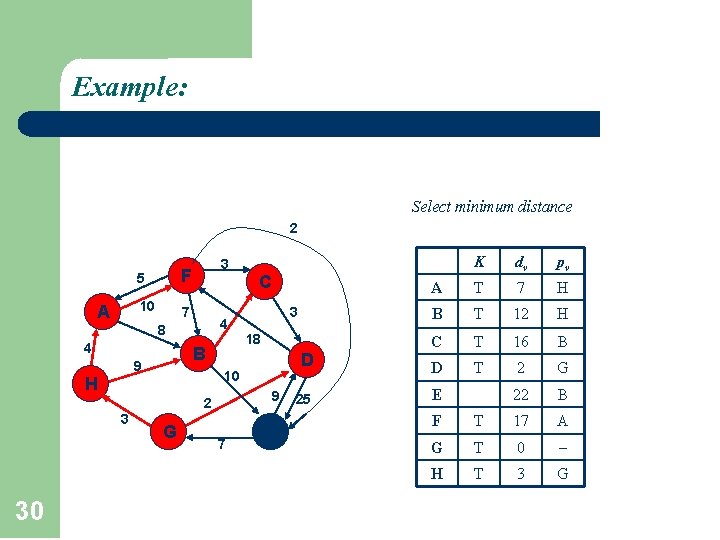
Example: Select minimum distance 2 A 5 F 10 7 C 4 8 4 B 9 18 D 9 2 30 3 10 H 3 G K dv pv A T 7 H B T 12 H C T 16 B D T 2 G 22 B 3 7 E 25 E F T 17 A G T 0 H T 3 G

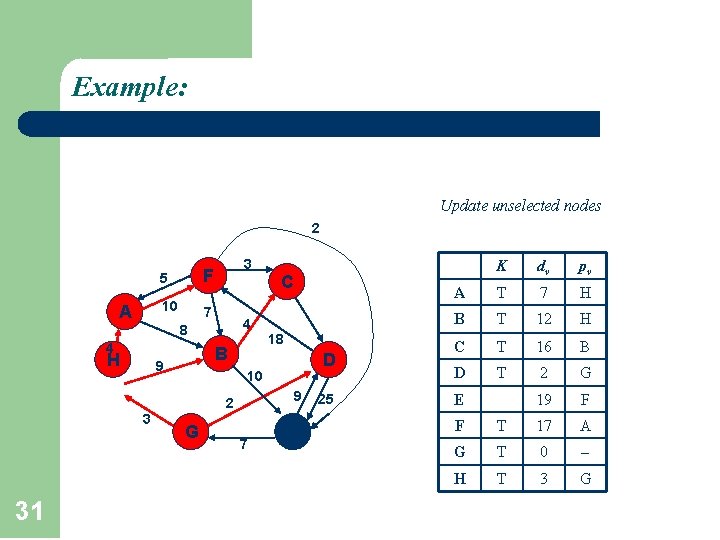
Example: Update unselected nodes 2 A 5 F 10 7 3 C 4 8 4 H B 9 31 D 10 9 2 3 18 G 7 E 25 K dv pv A T 7 H B T 12 H C T 16 B D T 2 G 19 F E F T 17 A G T 0 H T 3 G

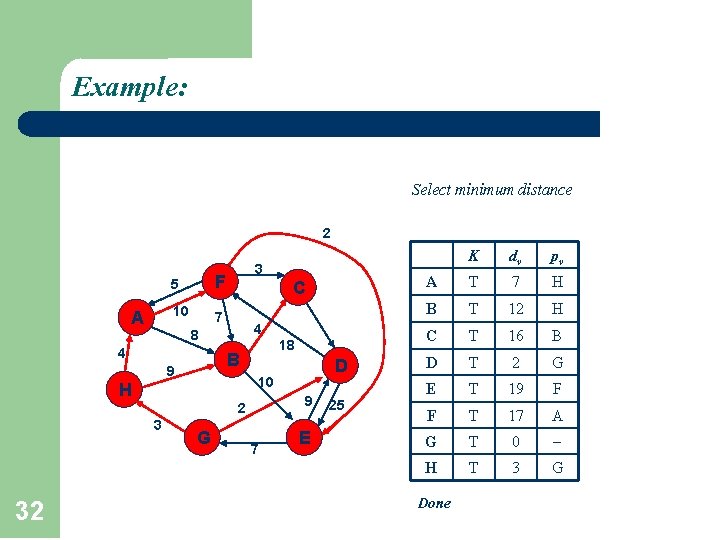
Example: Select minimum distance 2 A 5 F 10 7 3 C 4 8 4 B 9 9 2 32 D 10 H 3 18 G 7 E 25 K dv pv A T 7 H B T 12 H C T 16 B D T 2 G E T 19 F F T 17 A G T 0 H T 3 G Done

Order of Complexity l Analysis find. Min() takes O(V) time – outer loop iterates (V-1) times O(V 2) time – l l 33 Optimal for dense graphs, i. e. , |E| = O(V 2) Suboptimal for sparse graphs, i. e. , |E| = O(V)

Order of Complexity If the graph is sparse, i. e. , |E| = O(V) – maintain distances in a priority queue O(|E| log |V|) complexity 34

Summary In Kruskal algoritm, MST is form by taking small value edge which are already in sorted order. l Its complexity is O(|E| log|E|) l l l 35 Dijkstra algorithm will work especially for directed graphs. In Dijkstra algorithm, each node is visit and its neighbour nodes are expanded and then same process remain continue until all nodes visited.

In Next Lecture l 36 In next lecture, we will discuss about greedy algorithms and its types.