Lecture 21 Review Second order electrical circuits Series







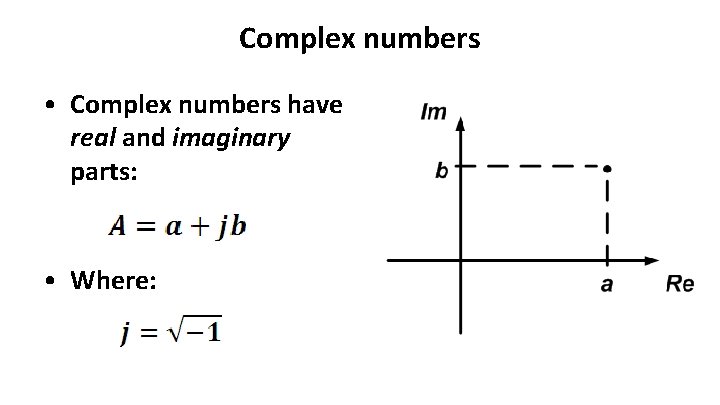







- Slides: 19

Lecture 21 • Review: Second order electrical circuits • Series RLC circuit • Parallel RLC circuit • Second order circuit natural response • Sinusoidal signals and complex exponentials • Related educational materials: –Chapter 8. 2, 8. 3

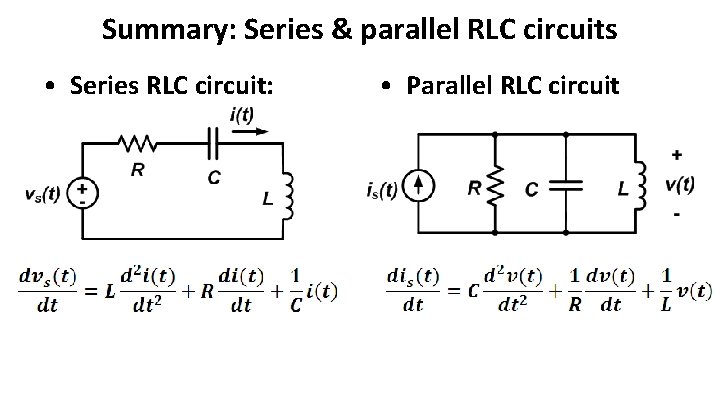
Summary: Series & parallel RLC circuits • Series RLC circuit: • Parallel RLC circuit

Second order input-output equations • In general, the governing equation for a second order system can be written in the form: • Where • is the damping ratio ( 0) • n is the natural frequency ( n 0)

Solution of second order differential equations • The solution of the input-output equation is (still) the sum of the homogeneous and particular solutions: • We will consider the homogeneous solution first:

Homogeneous solution (Natural response) • Assume form of solution: • Substituting into homogeneous differential equation: • We obtain two solutions:

Homogeneous solution – continued • Natural response is a combination of the solutions: • So that: • We need two initial conditions to determine the two unknown constants: • ,

Natural response – discussion • and n are both non-negative numbers – 1 solution composed of decaying exponentials – < 1 solution contains complex exponentials

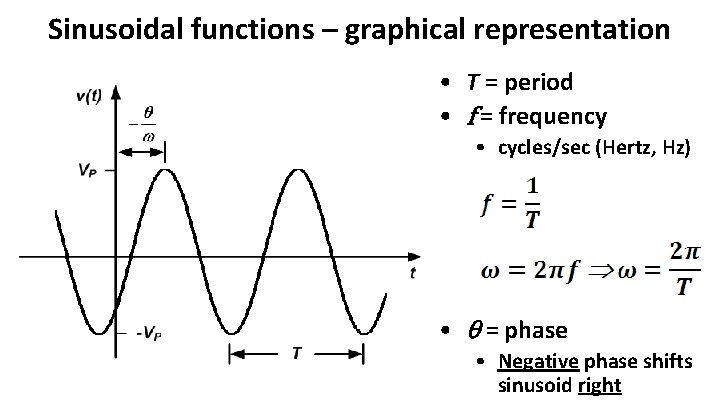
Sinusoidal functions • General form of sinusoidal function: • Where: – VP = zero-to-peak value (amplitude) – = angular (or radian) frequency (radians/second) – = phase angle (degrees or radians)

Sinusoidal functions – graphical representation • T = period • f = frequency • cycles/sec (Hertz, Hz) • = phase • Negative phase shifts sinusoid right
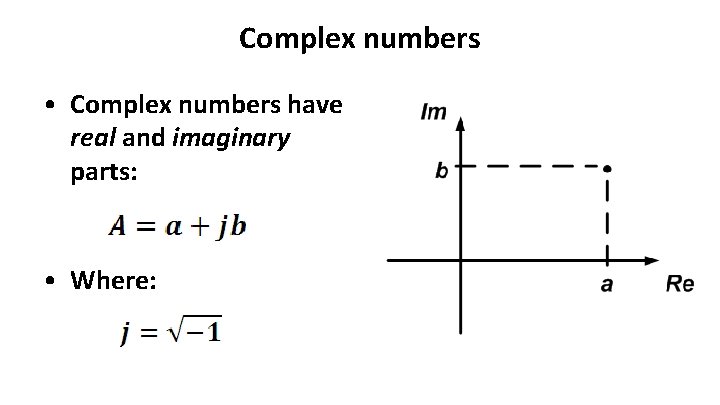
Complex numbers • Complex numbers have real and imaginary parts: • Where:

Complex numbers – Polar coordinates • Our previous plot was in rectangular coordinates • In polar coordinates: • Where:

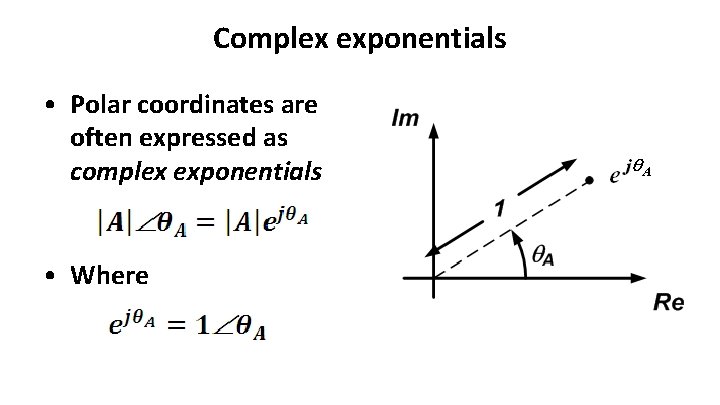
Complex exponentials • Polar coordinates are often expressed as complex exponentials • Where

Sinusoids and complex exponentials • Euler’s Identity:

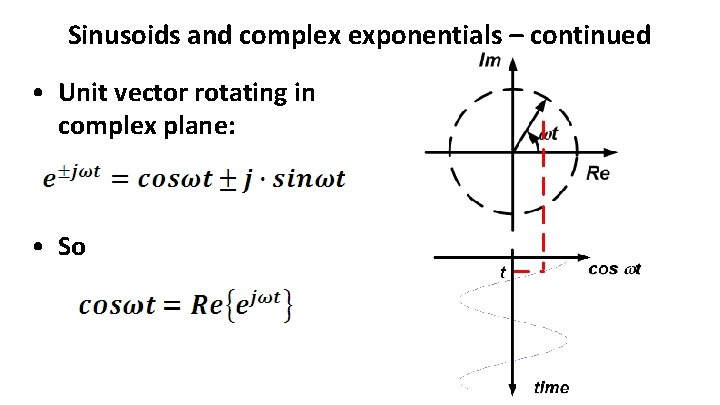
Sinusoids and complex exponentials – continued • Unit vector rotating in complex plane: • So

Complex exponentials – summary • Complex exponentials can be used to represent sinusoidal signals • Analysis is (nearly always) simpler with complex exponentials than with sines, cosines • Alternate form of Euler’s identity: • Cosines, sines can be represented by complex exponentials

Second order system natural response • Now we can interpret our previous result

Classifying second order system responses • Second order systems are classified by their damping ratio: • > 1 System is overdamped (the response consists of decaying exponentials, may decay slowly if is large) • < 1 System is underdamped (the response will oscillate) • = 1 System is critically damped (the response consists of decaying exponentials, but is “faster” than any overdamped response)

Note on underdamped system response • The frequency of the oscillations is set by the damped natural frequency, d
