Lecture 20 Stacks and Queues Stacks Queues and

Lecture 20 Stacks and Queues

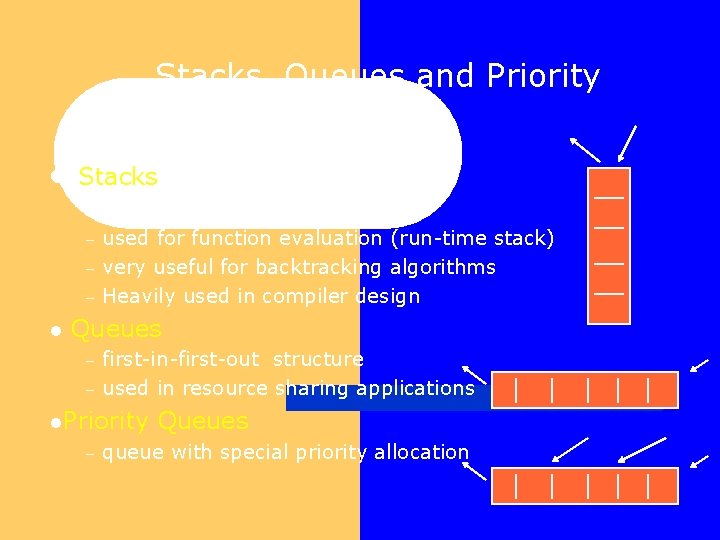
Stacks, Queues and Priority Queues l Stacks – – l first-in-last-out structure used for function evaluation (run-time stack) very useful for backtracking algorithms Heavily used in compiler design Queues – – first-in-first-out structure used in resource sharing applications l. Priority – Queues queue with special priority allocation

Stack Operations l Stack is a restricted data structure – – l data can only be added through the top (push) data can only be removed from the top (pop) Stack Data and Methods – container to hold the values of the stack l l – – – linked list vector/array push(value) - pushes the value into the stack (if not full) pop( ) - pops the top value of the stack (if not empty) top( ) - returns the top value of the stack empty() - returns true if empty full() - returns true if full clear() - clear the stack

Class Node class Node { int data; Node next; Node(int i, Node link) { data=I; next=link; } };

Linked List Implementation of Stack class Stack { public: // default constructor Stack () {Top= NULL ; size=0; } // accessors boolean Empty(); boolean Full() ; int Top. Of. Stack() ; // returns the top value of the stack int Size. Of. Stack() ; // returns the size of the stack // mutators void Push(int x); // push a value to the top of the stack boolean Pop(int x); // remove the most recent item void Clear(); // clear the entire stack private: Node Top; // is a pointer to the top element of the stack int size; };

Stack Method Implementations boolean Empty() { if (Top == null) return true; else return false; } Boolean Full() { if (size == Max. Size) return true; else return false; }

Stack Method Implementations ctd. . int Top. Of. Stack() { if (!Empty()) return Top. get. Data(); else System. out. println(“Stack is empty “) ; } Boolean Size. Of. Stack() { return size; }

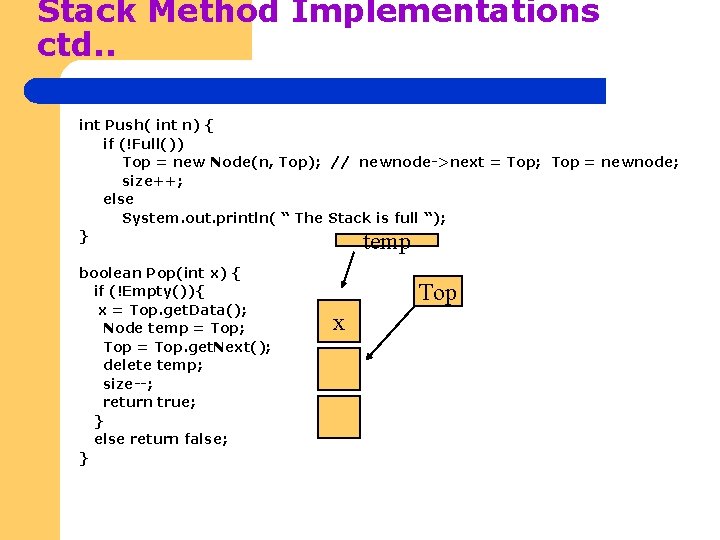
Stack Method Implementations ctd. . int Push( int n) { if (!Full()) Top = new Node(n, Top); // newnode->next = Top; Top = newnode; size++; else System. out. println( “ The Stack is full “); } temp boolean Pop(int x) { if (!Empty()){ x = Top. get. Data(); Node temp = Top; Top = Top. get. Next(); delete temp; size--; return true; } else return false; } Top x

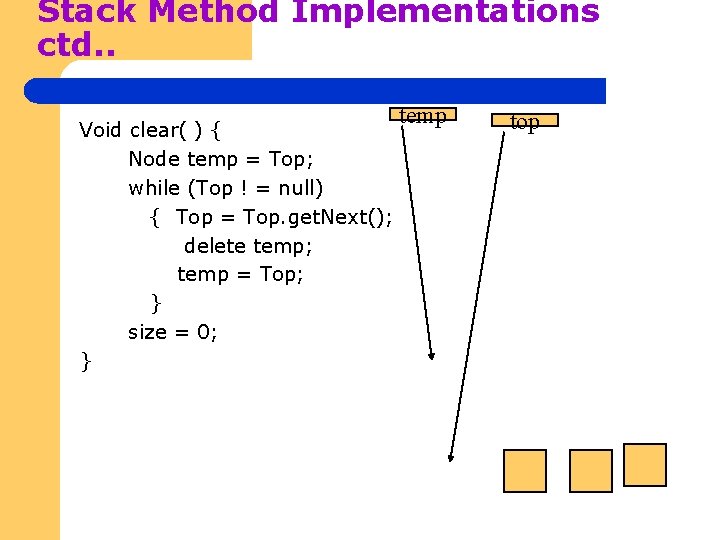
Stack Method Implementations ctd. . Void clear( ) { Node temp = Top; while (Top ! = null) { Top = Top. get. Next(); delete temp; temp = Top; } size = 0; } temp top

Queues l Behavior – – l Many Applications – – – l add item only from the back (enqueue) remove items only from the front (dequeue) printer queue network queues common resource sharing Queue Operations – – – enqueue dequeue clear empty full

Queue Implementation class Queue { public: Queue () {Front=null; Back=null; size=0; } // accessors boolean Empty() ; boolean Full() ; int Back. Of. Queue() ; // returns the back value of the queue int Front. Of. Queue() ; // returns the front value of the queue // mutators void Enqueue( int x); // add a value to the end of the queue boolean Dequeue(); // remove a value from the beginning of the queue void Clear(); // clear the entire queue private: Node Back; // is a pointer to the front element of the queue Node Front; // is a pointer to the back element of the stack int size; // holds the size of the queue };

Queue Method Implementation boolean Empty() { if (size==0) return true; else return false; } boolean Full() const { if (size == Max. Size) return true; else return false; } int Back. Of. Queue() { if (!Empty()) return Back. get. Data(); else System. out. println( “Queue is Empty “); }

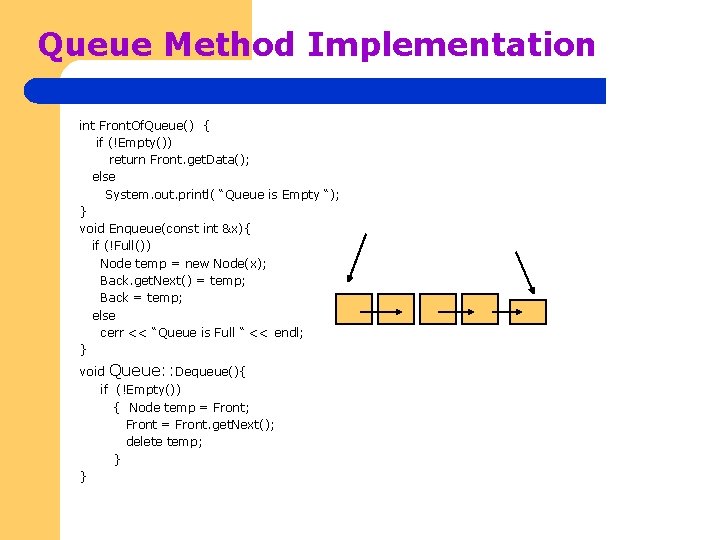
Queue Method Implementation int Front. Of. Queue() { if (!Empty()) return Front. get. Data(); else System. out. printl( “Queue is Empty “); } void Enqueue(const int &x){ if (!Full()) Node temp = new Node(x); Back. get. Next() = temp; Back = temp; else cerr << “Queue is Full “ << endl; } void Queue: : Dequeue(){ if (!Empty()) { Node temp = Front; Front = Front. get. Next(); delete temp; } }

Queue Method Implementation Void clear( ) { Node temp = Front; while (Front ! = null) { delete temp; Front = Front. get. Next(); temp = Front; } Back = null; size = 0; }