Lecture 20 parts A B First order circuit

Lecture 20 (parts A & B) • First order circuit step response • Nonzero initial conditions and multiple sources • Steady-state response and DC gain • Bias points and nominal operating conditions • Introduction to second order systems • Related educational materials: –Chapters 7. 5, 8. 1
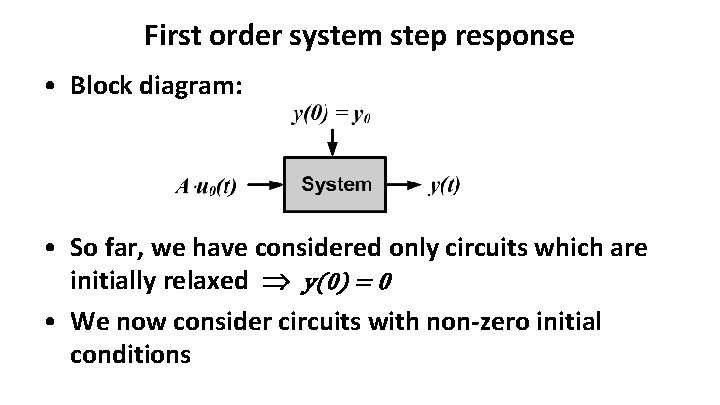
First order system step response • Block diagram: • So far, we have considered only circuits which are initially relaxed y(0) = 0 • We now consider circuits with non-zero initial conditions
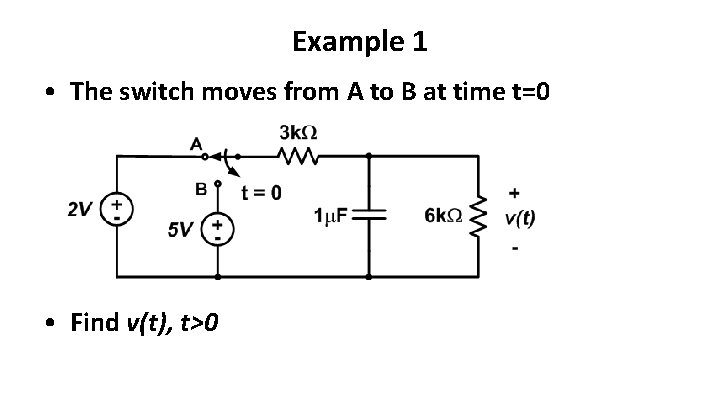
Example 1 • The switch moves from A to B at time t=0 • Find v(t), t>0

• Sketch input function on previous slide
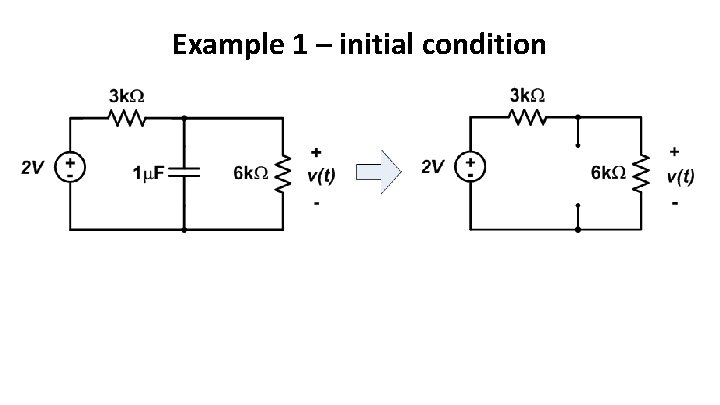
Example 1 – initial condition
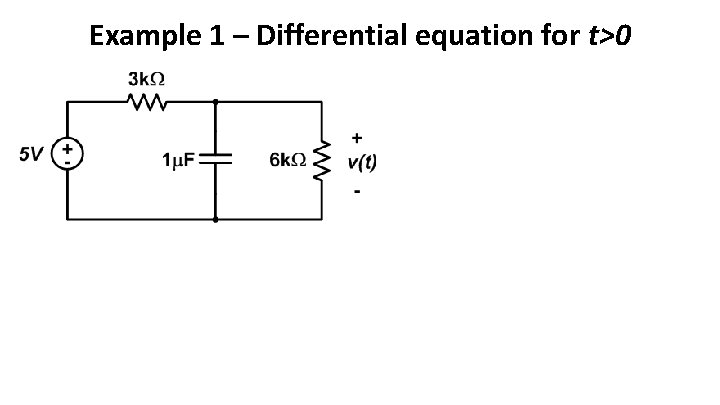
Example 1 – Differential equation for t>0
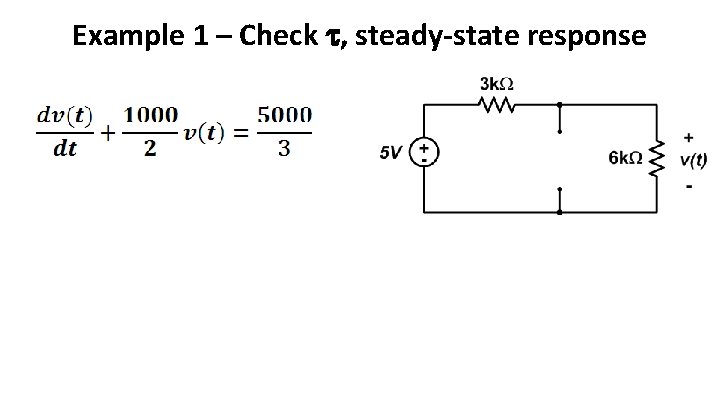
Example 1 – Check , steady-state response

Example 1 – circuit response • Differential equation: • Initial, final conditions: • Form of solution: ,

Example 1 – sketch input, output
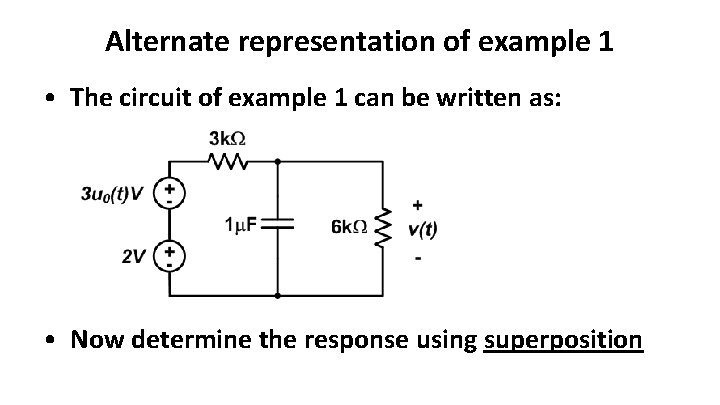
Alternate representation of example 1 • The circuit of example 1 can be written as: • Now determine the response using superposition

• Annotate previous slide to show input function
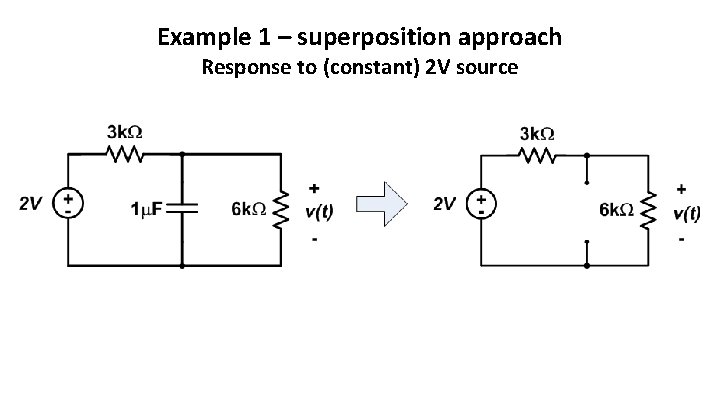
Example 1 – superposition approach Response to (constant) 2 V source
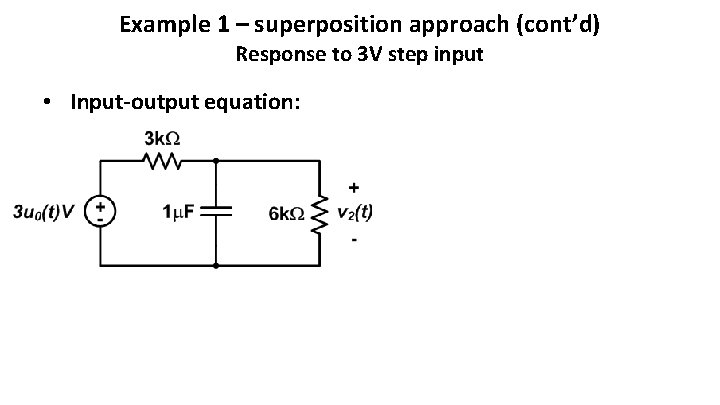
Example 1 – superposition approach (cont’d) Response to 3 V step input • Input-output equation:

Example 1 – superposition approach (cont’d) Response to 3 V step input • Governing equation: • Form of solution: • Initial condition: • Final condition:

Example 1 – superposition approach (cont’d) Overall response
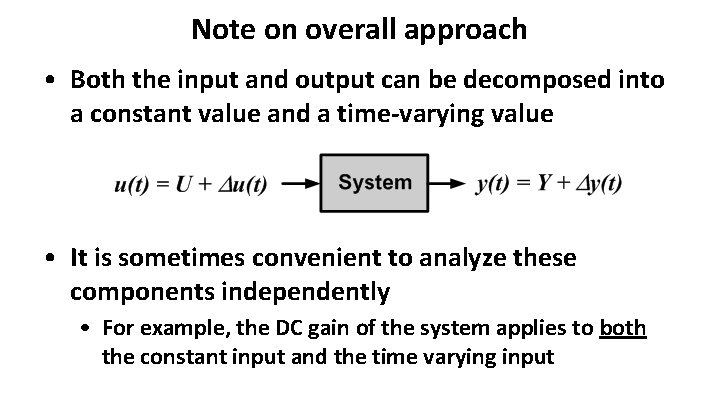
Note on overall approach • Both the input and output can be decomposed into a constant value and a time-varying value • It is sometimes convenient to analyze these components independently • For example, the DC gain of the system applies to both the constant input and the time varying input
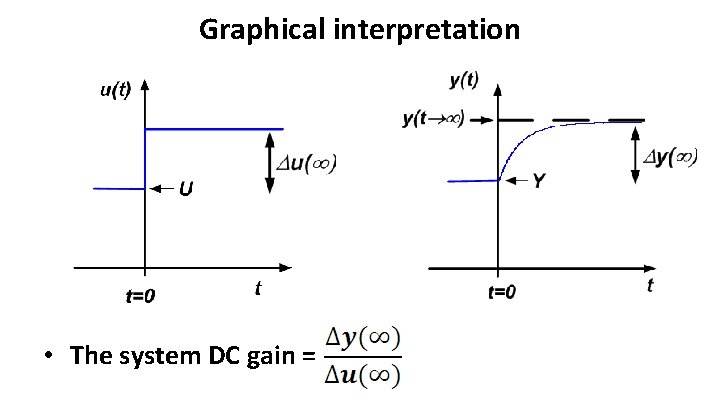
Graphical interpretation • The system DC gain =

Why is this approach useful? • Decomposing the input and output into constant and time-varying components can simplify analysis and interpretation of results • The constant part of the input and output is the bias point or nominal operating point • The system dynamic response is often characterized by the time-varying part of the input-output relationship • A nonlinear system, for example, can be approximated as a linear system with a bias point

Introduction to second order systems • Second order systems are governed by second order differential equations • Input-output relation contains a second order derivative term, but no derivatives higher than second order • The physical system has two independent energy storage elements • The natural response of a second order system can oscillate with time (but doesn’t necessarily have to) • The response can overshoot its final value


Introduction to second order systems – continued • The oscillations in the natural response are due to energy being traded between the energy storage elements • Increasing energy dissipation reduces the amplitude of the oscillations (the system is said to be more highly damped) • If energy dissipation is above a critical value, the response will no longer oscillate • In general, increasing the energy dissipation will also cause the system to respond to changes more “slowly”


• On previous slide, talk about damping and energy dissipation – Example: suspension system in car
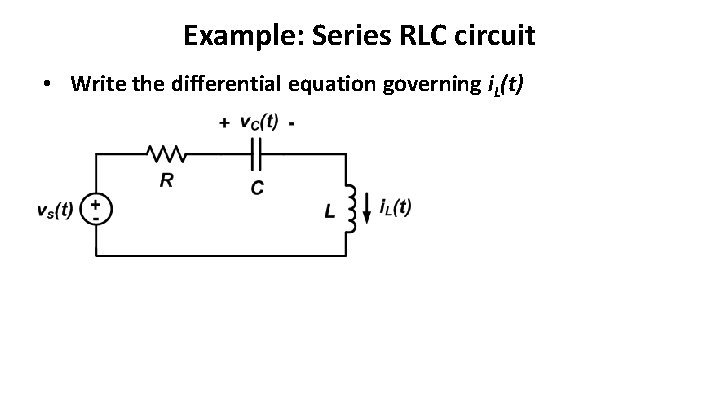
Example: Series RLC circuit • Write the differential equation governing i. L(t)

Series RLC circuit – continued
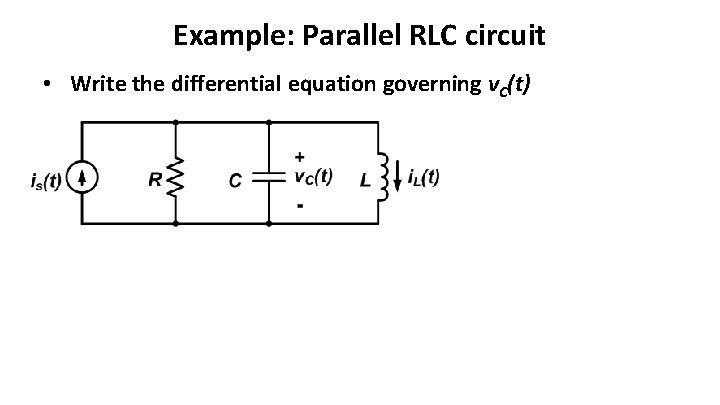
Example: Parallel RLC circuit • Write the differential equation governing v. C(t)

Parallel RLC circuit – continued

- Slides: 28