Lecture 2 Sampling design Analysis of data 1




















- Slides: 24

Lecture 2 • Sampling design • Analysis of data. 1

The sampling design, - the what, the where, and the how. . • The methodology section should in principle enable results to be replicated! • Can you compile a complete data set? • The method used for deciding which member of a statistical population will be included in the sample is called the sampling design. 2

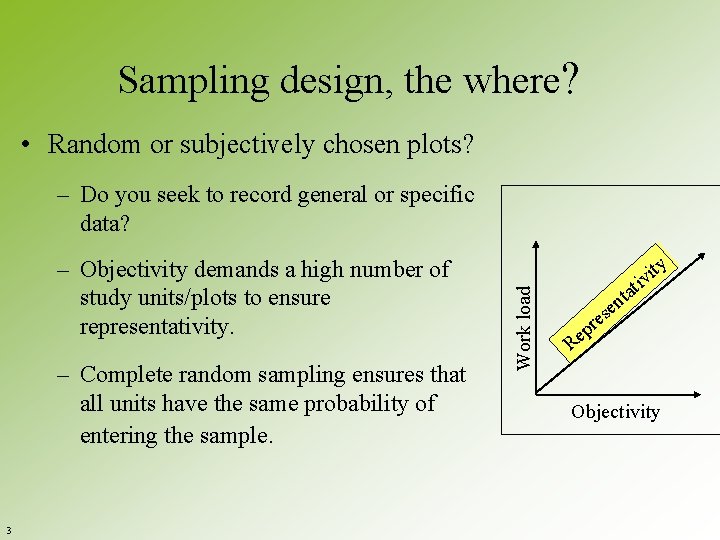
Sampling design, the where? • Random or subjectively chosen plots? – Objectivity demands a high number of study units/plots to ensure representativity. – Complete random sampling ensures that all units have the same probability of entering the sample. 3 Work load – Do you seek to record general or specific data? ty i v i se e r ep at t n R Objectivity

Sampling design, the where? • Statistical qualities of plots /study units, are the plots independent? • Lumping of plots? – How could lumping of plots have effected the results in the study by Peres et al. (the study of Brazil nut)? • Redundancy – are common types too redundant (common)? • Are rare types represented among the samples? 4

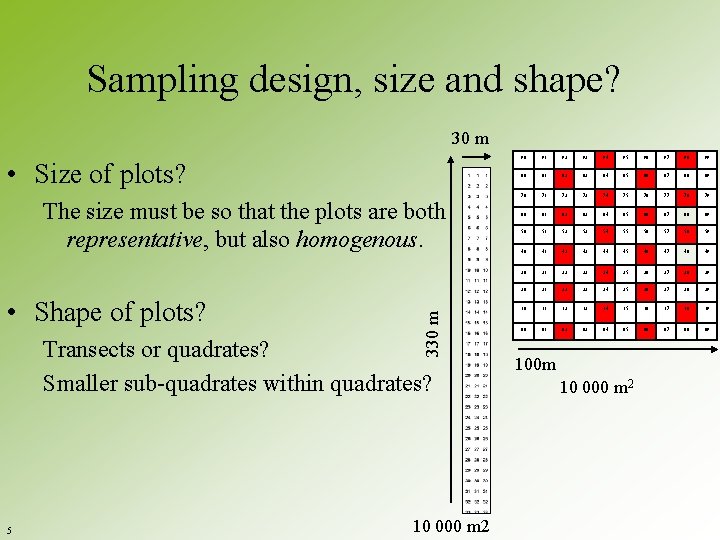
Sampling design, size and shape? 30 m • Size of plots? • Shape of plots? 330 m The size must be so that the plots are both representative, but also homogenous. Transects or quadrates? Smaller sub-quadrates within quadrates? 5 10 000 m 2 90 91 92 93 94 95 96 97 98 99 80 81 82 83 84 85 86 87 88 89 70 71 72 73 74 75 76 77 78 79 60 61 62 63 64 65 66 67 68 69 50 51 52 53 54 55 56 57 58 59 40 41 42 43 44 45 46 47 48 49 30 31 32 33 34 35 36 37 38 39 20 21 22 23 24 25 26 27 28 29 10 11 12 13 14 15 16 17 18 19 00 01 02 03 04 05 06 07 08 09 100 m 10 000 m 2

Sampling design, how many? • How many plots / study units? – High variation requires a higher number of plots/study units. – As many as you can… • Permanent plots? – Do you want to revisit? For other scientists to revisit? – Metal bars in the soil, metal tags on trees etc. , what more. . • Remember that several statistical analyses assume random sampling! 6

Sampling design, the what? qualitative and quantitative approaches. • Qualitative and quantitative approaches work together, both may be important in a study. In what way? – Qualitative approaches are useful and necessary for in depth knowledge of a situation, or when describing the study area or units of research, – Quantitative approaches is useful for more objective comparison of different systems, and may enable statistical analysis. 7

The data, quantitative approaches • Examples of explanatory variables, data to collect: soil variables (moisture, soil type, and more), aspect, shadow sun , income, parents occupation. . • Data collected /ecological variables must be tied directly to the sample plots /sample units. • All variables within a category must be quantified with the same unit in the study. • A questionnaire in social science may give quantitative variables. 8

The data, qualitative approaches. Observations, important in every discipline (ranging from non-participant to participant). – Interviews (ranging from semi-structured to open-ended). • Open ended, initial interviews – Documents • Private – public. – Audio visual (including materials such as photographs, compact disks and videotapes). 9

Analysis of data • The purpose of analysing the data is explore different, interesting characteristics inherent in the results. • Characteristics that the study units have in common. • Characteristics that the study units are different from. 10

Analysis, categorization • Categorization is the way that something is divided up into a set off of different classes. • Selecting categories. • Value can be assigned to different categories • Beware of units and scales, need to be the same. 11

Analysing quantitative forms of data. • In ecology: calculate the density, frequency, dominance, etc. • In social sciences: demography – age classes, percentage of ethnic people in the community, etc. 12

Analysis of data • Graphical presentation – Tables and figures; permits us to present a simplified version of the results. – Graphs, typically relate two dimensions such as quantity of time. – Graphs show trends or movements over time. 13

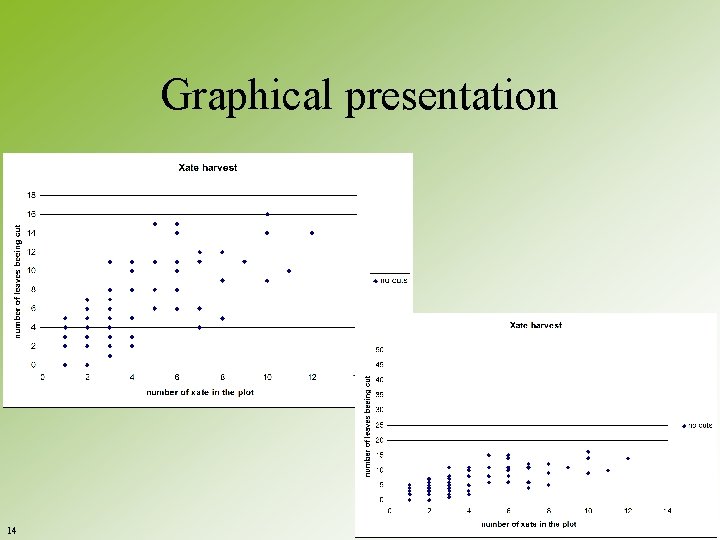
Graphical presentation 14

Analysis of data • An important tool for analyzing data is statistics, a mathematical way of summarizing and interpreting quantifiable research results. • Does the study allow for statistics? • It is important to understand when to apply each statistical tool, and how to interpret the results. 15

Statistical analysis of data • Everything varies, if you measure two things twice they will be different. • Thus, finding that things varies is simply not interesting. That is why statistics are needed. • If we measure bigger differences than would have expected by chance, then we say that the result is statistically significant. • So, why doesn’t all research projects use statistics? 16

The LUPIS project LUPIS will assess the strengths and weaknesses of new policies prior to their introduction, i. e. ex -ante impact assessment through the use and development of tools and models. -The project will test the validity of existing modelling tools used in the European context. Brazil Mali - Models are data intensive, often data generalised for a larger region is used. - What aspects should be considered when discussing model results in relation to the aim of sustainable development? China

An example, a research project “Poverty has been a major barrier to a healthy lifestyle”. The abstract • The elderly have chronic health problems attributed to obesity. • Research suggests that exercise can reduce the risk of some health problems. • The hypothesis of the study: “that older African American women living above the poverty level will practice more health promoting behaviours as measured by the Health. Promoting Lifestyle profile (HPLP) than women living below the poverty level.

The method, including the instruments and procedure. • What were good aspects of the design? Could there be aspects of bias in the design? • What were questionable aspects of the design? What factors other than the projects might have resulted in positive attitudes.

Results • Try to evaluate the results! – Are the presented results supported by the study? – Do the results answer the purpose of the study? – Important part of interpreting the results - Do tables and figures present the results in a comprehendible way? – Are some results missing, are results confounding? – Look for speculation only!

Results, the example – Results lacking, would have been informative! • What percentage of those above poverty level had been graduated from college and high school. • A large percentage were married or widowed, but we don’t know their economic level. • Those below the poverty level had a large range of scores, along with greater variability.

Discussion • Finally you will evaluate the experimentor’s discussion of the results in terms of the extent to which the conclusion is justified, can be generalized and has limitations. • Statements – are they justified? – Look out for statements of which there is no good arguments based on own results. – Or statements where references are lacking.

Discussion / conclusion, the example • The conclusion is inappropriate! – Health-promoting behaviors were not observed. , they were reported. – we don’t know the extent to which test items accurately reflect behavior. – we don’t know the accuracy of the self-reports – Note that score might have been higher if all forms of exercise, not just recreational were reported.

Conclusion, the example • This is misleading, because it implies that exercise is a main factor that accounts for the difference in HPLP between the two groups. • Thus if groups were matched on all non-poverty level variables and were tested by a naive (with respect to the purpose of the study) individual, it would be possible to reach a valid conclusion.