Lecture 2 Replication and pseudoreplication This lecture will

Lecture 2: Replication and pseudoreplication

This lecture will cover: • Experimental units (replicates) • Pseudoreplication • Degrees of freedom

Experimental unit Scale at which independent applications of the same treatment occur Also called “replicate”, represented by “n” in statistics

Experimental unit Example: Effect of fertilization on caterpillar growth

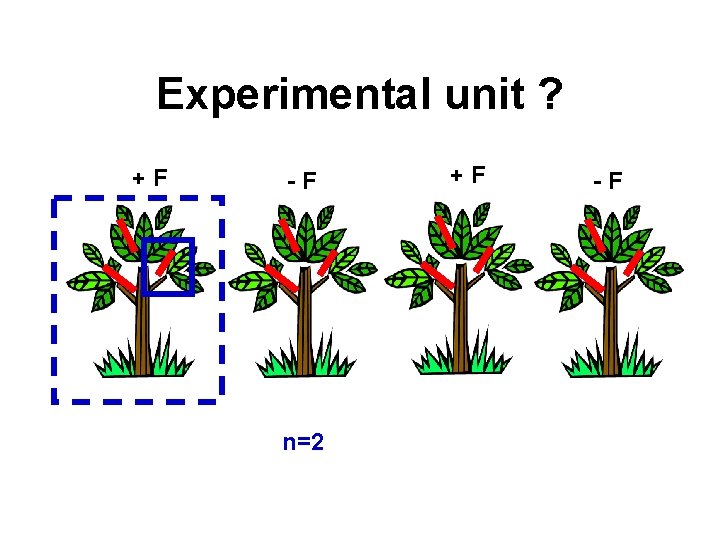
Experimental unit ? +F -F n=2 +F -F

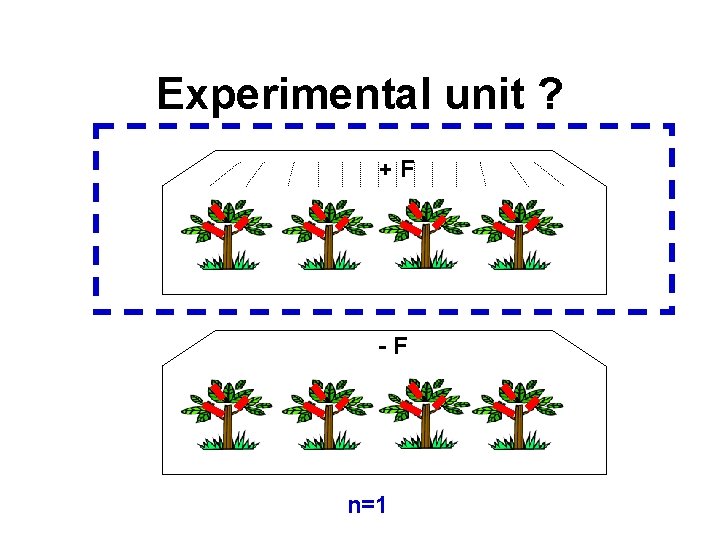
Experimental unit ? +F -F n=1

Pseudoreplication Misidentifying the scale of the experimental unit; Assuming there are more experimental units (replicates, “n”) than there actually are

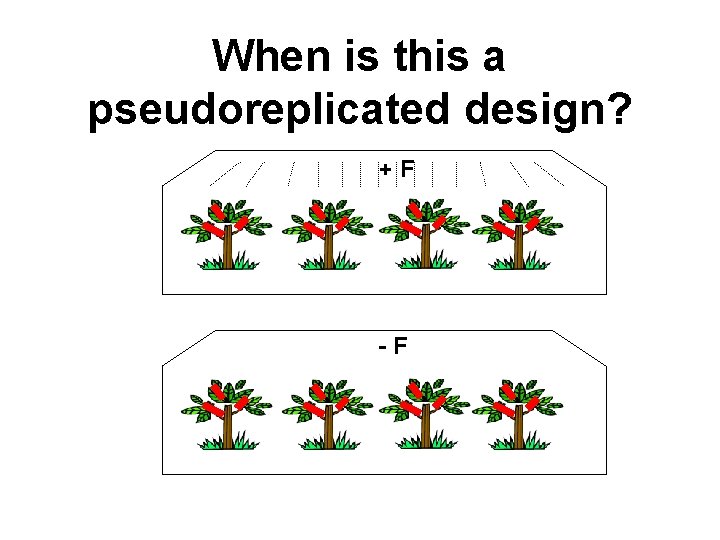
When is this a pseudoreplicated design? +F -F

Example 1. Hypothesis: Insect abundance is higher in shallow lakes

Example 1. Experiment: Sample insect abundance every 100 m along the shoreline of a shallow and a deep lake

Example 2. What’s the problem ? Spatial autocorrelation

Example 2. Hypothesis: Two species of plants have different growth rates

Example 2. Experiment: • Mark 10 individuals of sp. A and 10 of sp. B in a field. • Follow growth rate over time If the researcher declares n=10, could this still be pseudoreplicated?

Example 2.

Example 2. time

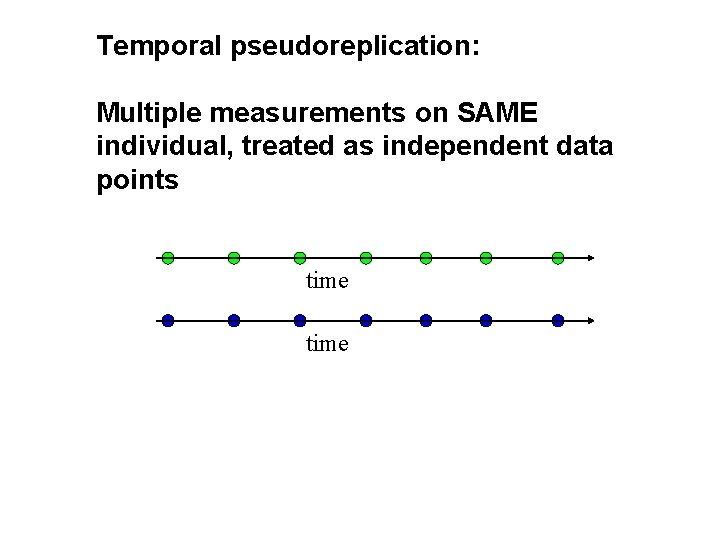
Temporal pseudoreplication: Multiple measurements on SAME individual, treated as independent data points time

Spotting pseudoreplication 1. Inspect spatial (temporal) layout of the experiment 2. Examine degrees of freedom in analysis

Degrees of freedom (df) Number of independent terms used to estimate the parameter = Total number of datapoints – number of parameters estimated from data

Example: Variance If we have 3 data points with a mean value of 10, what’s the df for the variance estimate? Independent term method: Can the first data point be any number? Yes, say 8 Can the second data point be any number? Yes, say 12 Can the third data point be any number? No – as mean is fixed ! Variance is (y – mean)2 / (n-1)

Example: Variance If we have 3 data points with a mean value of 10, what’s the df for the variance estimate? Independent term method: Therefore 2 independent terms (df = 2)

Example: Variance If we have 3 data points with a mean value of 10, what’s the df for the variance estimate? Subtraction method Total number of data points? 3 Number of estimates from the data? 1 df= 3 -1 = 2

Example: Linear regression Y = mx + b Therefore 2 parameters estimated simultaneously (df = n-2)

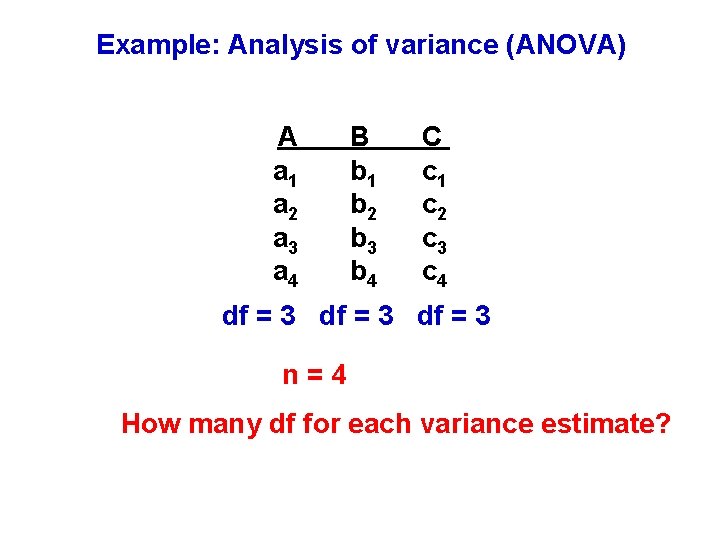
Example: Analysis of variance (ANOVA) A a 1 a 2 a 3 a 4 B b 1 b 2 b 3 b 4 C c 1 c 2 c 3 c 4 What is n for each level?

Example: Analysis of variance (ANOVA) A a 1 a 2 a 3 a 4 B b 1 b 2 b 3 b 4 C c 1 c 2 c 3 c 4 df = 3 n=4 How many df for each variance estimate?

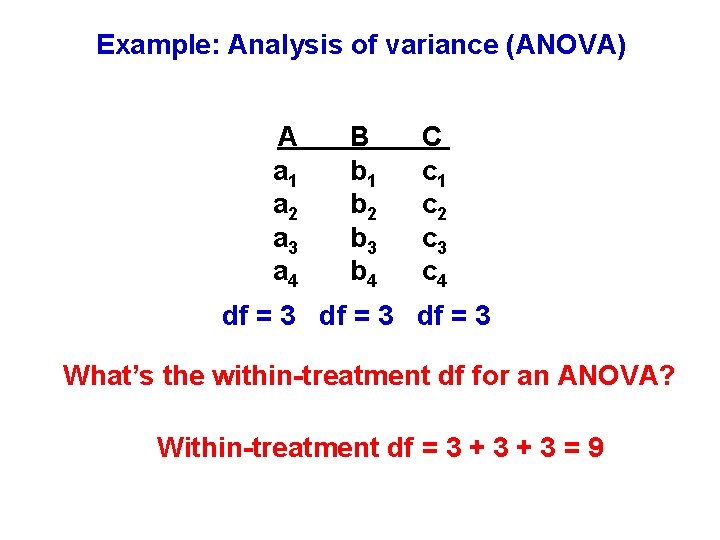
Example: Analysis of variance (ANOVA) A a 1 a 2 a 3 a 4 B b 1 b 2 b 3 b 4 C c 1 c 2 c 3 c 4 df = 3 What’s the within-treatment df for an ANOVA? Within-treatment df = 3 + 3 = 9

Example: Analysis of variance (ANOVA) A a 1 a 2 a 3 a 4 B b 1 b 2 b 3 b 4 C c 1 c 2 c 3 c 4 If an ANOVA has k levels and n data points per level, what’s a simple formula for within-treatment df? df = k(n-1)

Spotting pseudoreplication An experiment has 10 fertilized and 10 unfertilized plots, with 5 plants per plot. The researcher reports df=98 for the ANOVA (within-treatment MS). Is there pseudoreplication?

Spotting pseudoreplication An experiment has 10 fertilized and 10 unfertilized plots, with 5 plants per plot. The researcher reports df=98 for the ANOVA. Yes! As k=2, n=10, then df = 2(10 -1) = 18

Spotting pseudoreplication An experiment has 10 fertilized and 10 unfertilized plots, with 5 plants per plot. The researcher reports df=98 for the ANOVA. What mistake did the researcher make?

Spotting pseudoreplication An experiment has 10 fertilized and 10 unfertilized plots, with 5 plants per plot. The researcher reports df=98 for the ANOVA. Assumed n=50: 2(50 -1)=98

Why is pseudoreplication a problem? Hint: think about what we use df for!

How prevalent? Hurlbert (1984): 48% of papers Heffner et al. (1996): 12 to 14% of papers