Lecture 2 Read textbook CHAPTER 1 4 Apps

Lecture 2 Read textbook CHAPTER 1. 4, Apps B&D Today: Derive EOMs & Linearization Fundamental equation of motion for mass-springdamper system (1 DOF). Linear and nonlinear system. Examples of derivation of EOMs Appendix A Equivalence of principles of conservation of mechanical energy and conservation of linear momentum. Appendix B: Linearization Work problems: Chapter 1: 5, 8, 13, 14, 15, 20, 43, 44, 56 1

Lecture 2 ME 617 Kinetics of 1 -DOF mechanical systems The fundamental elements in a M mechanical system and the K C process to set a coordinate system and derive an equation of motion. LINEARIZATION included. 2014 Luis San Andres© Luis San Andres Texas A&M University 2

A system with an elastic element (linear spring)
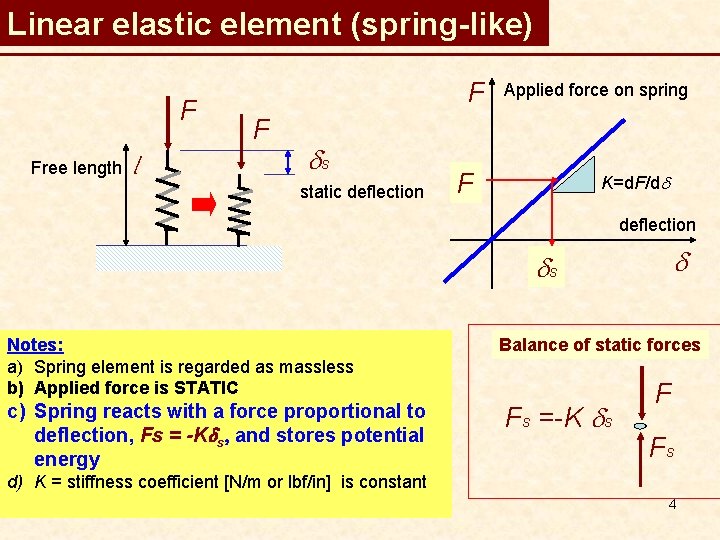
Linear elastic element (spring-like) F Free length l F F ds static deflection Applied force on spring F K=d. F/dd deflection d ds Notes: a) Spring element is regarded as massless b) Applied force is STATIC c) Spring reacts with a force proportional to deflection, Fs = -Kds, and stores potential energy Balance of static forces Fs =-K ds F Fs d) K = stiffness coefficient [N/m or lbf/in] is constant 4

Statics of system with elastic & mass elements

Linear spring + added weight W Free length F W l ds static deflection Reaction force from spring W K=d. F/dd static deflection ds Notes: a) Block has weight W= Mg b) Block is regarded as a point mass Balance of static forces W=Fs = K ds d W Fs 6

Dynamics of system with elastic & mass elements Derive the equation of motion (EOM) for the system

Linear spring + weight (mass x g ) + force F(t) Free length W l F W+F(t) Reaction force from spring W+F ds K=d. F/dd SEP dynamic deflection ds+X(t) Notes: a) Coordinate X describing motion has origin at Static Equilibrium Position (SEP) b) For free body diagram, assume state of motion, for example X(t)>0 c) Then, state Newton’s equation of motion d) Assume no lateral (side motions) d X+ds Free Body diagram W+F M acceleration M Ax = W+F - Fspring 8

Derive the equation of motion W+F M Ax = W+F - Fspring ds Free length SEP l ds+X(t) FBD: X>0 W+F M Fspring X(t) Fspring = K(X+ds ) M Ax = W+F – K(X+ds) M Ax = ( W-Kds) +F – KX Cancel terms from force balance at SEP to get M Ax = +F – KX M Ax + K X= F(t) 9 Note: Motions from SEP
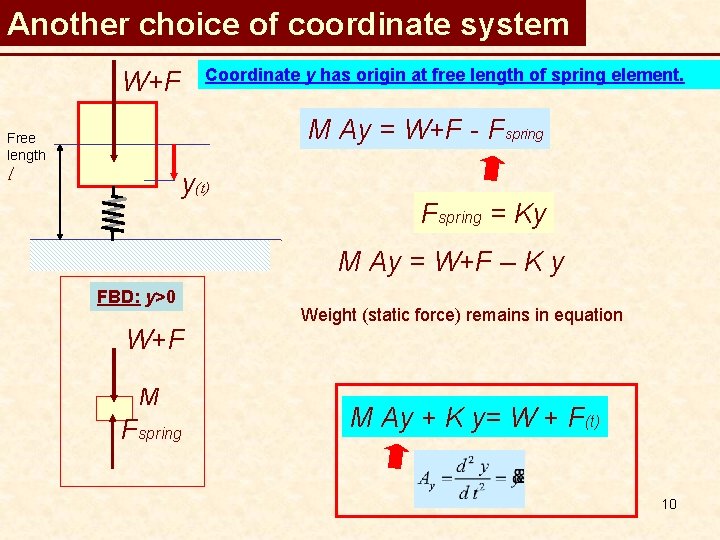
Another choice of coordinate system Coordinate y has origin at free length of spring element. W+F M Ay = W+F - Fspring Free length l y(t) Fspring = Ky M Ay = W+F – K y FBD: y>0 W+F M Fspring Weight (static force) remains in equation M Ay + K y= W + F(t) 10

EOM in two coordinate systems W+F Free length l M Ay + K y = W + F(t) (1) ds SEP y(t) X(t) M Ax + K X= F(t) (2) y = X+ ds Fspring = Ky = K(X+ ds ) Coordinate y has origin at free length of spring element. X has origin at SEP. (? ) Are Eqs. (1) and (2) the same? (? ) Do Eqs. (1) and (2) represent the same system? (? ) Does the weight disappear? (? ) Can I just cancel the weight? 11

K-M system with dissipative element (a viscous dashpot) Derive the equation of motion (EOM) for the system
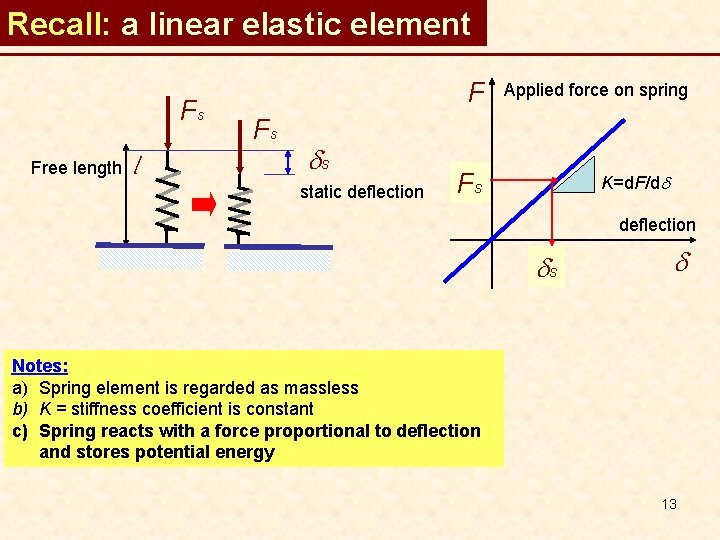
Recall: a linear elastic element Fs Free length l F Fs ds static deflection Applied force on spring Fs K=d. F/dd deflection ds d Notes: a) Spring element is regarded as massless b) K = stiffness coefficient is constant c) Spring reacts with a force proportional to deflection and stores potential energy 13

(Linear) viscous damper element F F F V velocity F Applied force on damper D=d. F/d. V velocity V Notes: a) Dashpot element (damper) is regarded as massless b) D = damping coefficient [N/(m/s) or lbf/(in/s) ] is constant c) A damper needs velocity to work; otherwise it can not dissipate mechanical energy d) Under static conditions (no motion), a damper does NOT react with a force 14
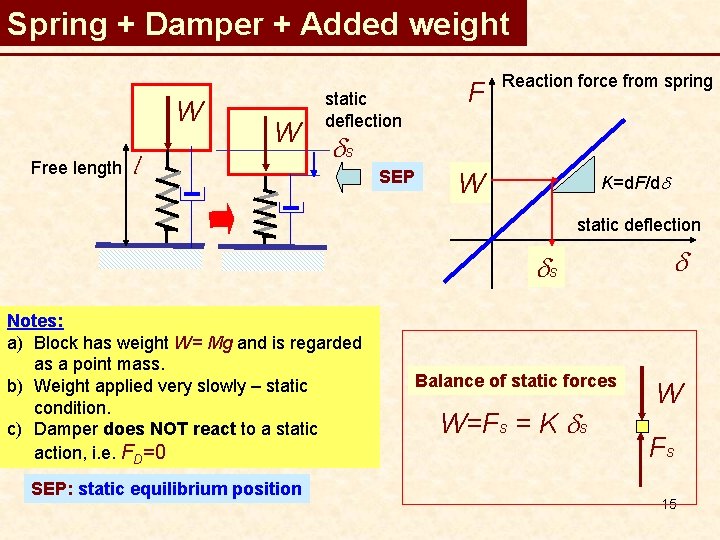
Spring + Damper + Added weight W Free length W l static deflection F Reaction force from spring ds SEP W K=d. F/dd static deflection ds Notes: a) Block has weight W= Mg and is regarded as a point mass. b) Weight applied very slowly – static condition. c) Damper does NOT react to a static action, i. e. FD=0 SEP: static equilibrium position Balance of static forces W=Fs = K ds d W Fs 15
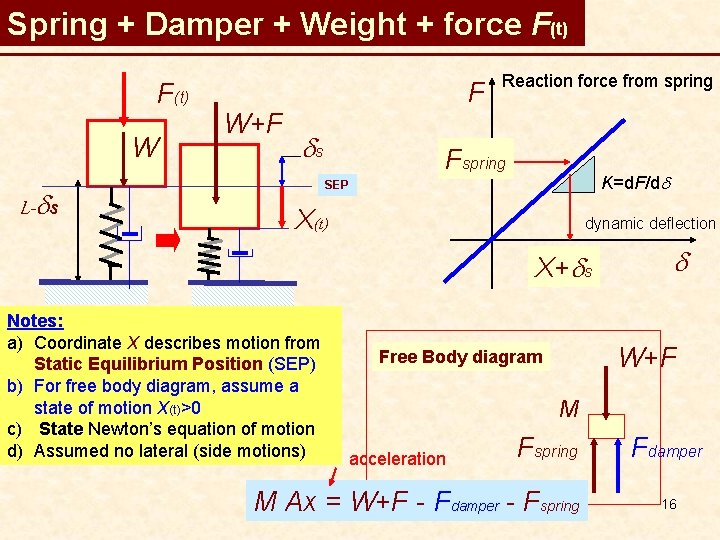
Spring + Damper + Weight + force F(t) W L-ds W+F F ds Reaction force from spring Fspring K=d. F/dd SEP X(t) dynamic deflection X+ds Notes: a) Coordinate X describes motion from Static Equilibrium Position (SEP) b) For free body diagram, assume a state of motion X(t)>0 c) State Newton’s equation of motion d) Assumed no lateral (side motions) d W+F Free Body diagram M acceleration Fspring M Ax = W+F - Fdamper - Fspring Fdamper 16

Equation of motion: spring-damper-mass W+F M Ax = W+F(t) - Fdamper - Fspring Fdamper = D VX SEP L-ds X(t) K Fspring = K(X+ ds ) D M Ax = W+F – K(X+ds) – D VX FBD: X>0 W+F M Fspring Fdamper M Ax = ( W-Kds) +F – KX - DVX Cancel terms from force balance at SEP to get M Ax = +F – KX – D VX M Ax + DVX + K X = F(t) EOM: Notes: Motions from SEP 17

Simple nonlinear mechanical system Derive the equation of motion (EOM) for the system and linearize EOM about SEP
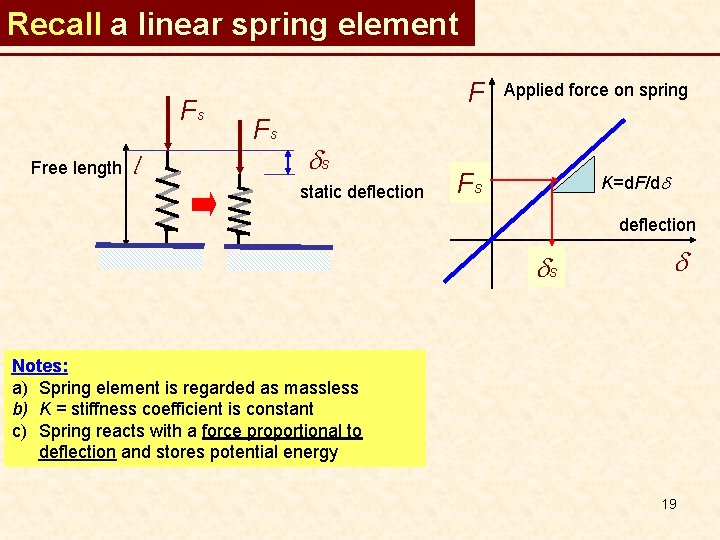
Recall a linear spring element Fs Free length l F Fs ds static deflection Applied force on spring Fs K=d. F/dd deflection ds d Notes: a) Spring element is regarded as massless b) K = stiffness coefficient is constant c) Spring reacts with a force proportional to deflection and stores potential energy 19
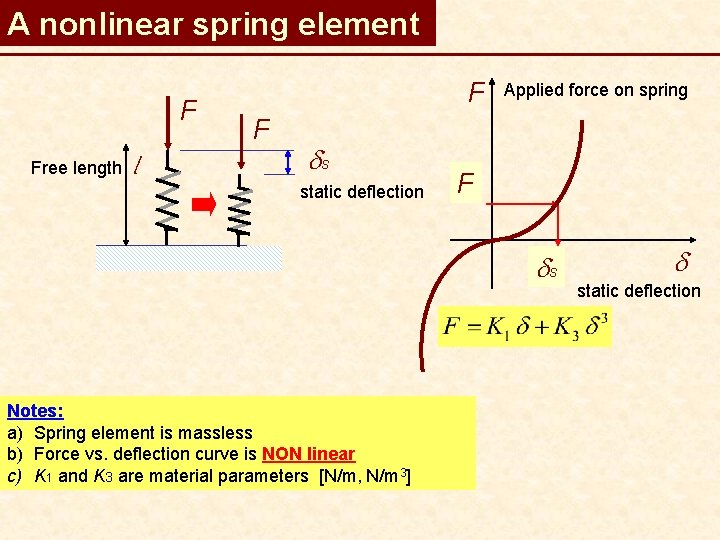
A nonlinear spring element F Free length l F F ds static deflection Applied force on spring F ds Notes: a) Spring element is massless b) Force vs. deflection curve is NON linear c) K 1 and K 3 are material parameters [N/m, N/m 3] d static deflection
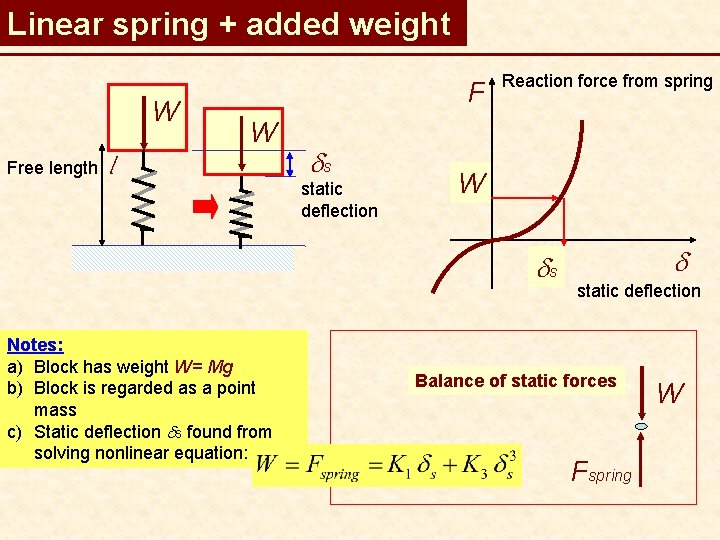
Linear spring + added weight W Free length F W l ds static deflection Reaction force from spring W ds Notes: a) Block has weight W= Mg b) Block is regarded as a point mass c) Static deflection ds found from solving nonlinear equation: d static deflection Balance of static forces Fspring W
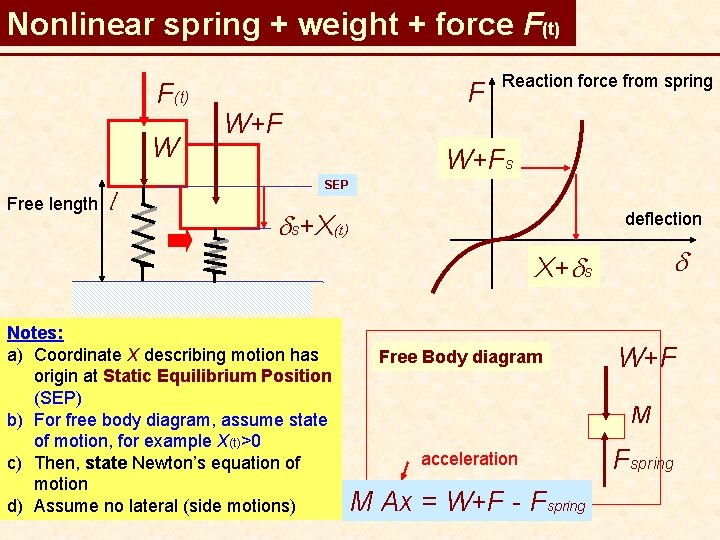
Nonlinear spring + weight + force F(t) W Free length l F W+F Reaction force from spring W+Fs SEP ds+X(t) deflection d X+ds Notes: a) Coordinate X describing motion has origin at Static Equilibrium Position (SEP) b) For free body diagram, assume state of motion, for example X(t)>0 c) Then, state Newton’s equation of motion d) Assume no lateral (side motions) Free Body diagram W+F M acceleration M Ax = W+F - Fspring

Nonlinear Equation of motion W+F Free length SEP ds+X(t) l Expand RHS: FBD: X>0 W+F M Cancel terms from force balance at SEP to get Fspring Notes: Motions are from SEP

Linearize equation of motion W+F EOM is nonlinear: SEP Free length ds+X(t) l Assume motions X(t) << ds which means |F(t)| << W and set X 2 ~0, X 3~0 FBD: X>0 to obtain the linear EOM: W+F M Fspring where the linearized stiffness is a function of the static condition
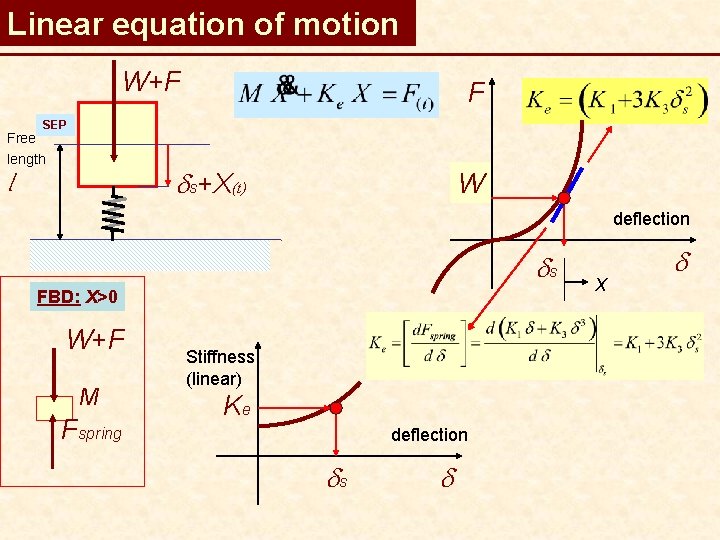
Linear equation of motion W+F F SEP Free length ds+X(t) l W deflection ds FBD: X>0 W+F M Fspring Stiffness (linear) Ke deflection ds d X d

Read & rework Examples of derivation of EOMS for physical systems available on class URL site(s) 2014 Luis San Andres©
- Slides: 26