Lecture 2 Producing Brine EAS 7970 Multiphase Subsurface

Lecture 2: Producing Brine EAS 7970: Multiphase Subsurface Fluid Flow L. M. Cathles Tammo Steenhuis Larry Brown Spring 2017 3160 Snee Hall

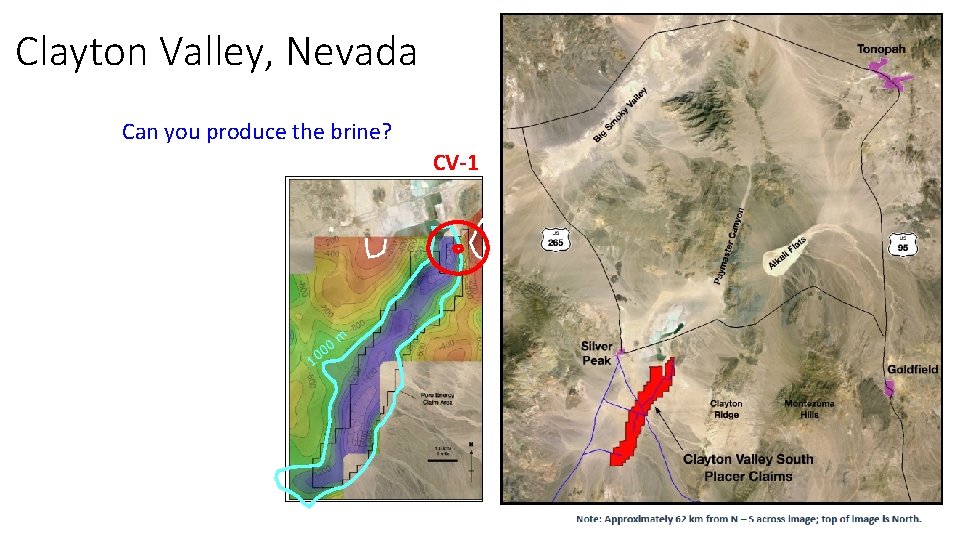
Clayton Valley, Nevada Can you produce the brine? CV-1 m 1 0 00

Li Brine Fresh water Pump test: pump 14 inch well diameter Perforated interval 116 m

Theory Darcy’s Law Continuity equation Chain rule rock compressibility Constitutive relations water compressibility specific storage Define: S=Ssb, and T=Kb Diffusion equation Storativity and transmissability Final pumping equations

The solution for a confined aquifer is the Theis equation Theis solution confined aquifer pumped at constant rate The well function transmissivity storativity

The well function is tabulated As t gets large, W→ limit Which means drawdown becomes ~ constant 1/u → Note: It W=4π, Dht→large = Q/T. Thus, T estimates long term drawdown

A little mathematics is very useful… Series expansion 1 st two terms very good approximation for u<~0. 1 Thus: u ln 1/1. 78 u sum to n=3 sum to n=5 Sum to n=20 W(u) 5 -1. 91 3. 50 2. 205 0. 0011 1 -0. 5766 0. 228 0. 219 0. 1 1. 725 1. 82 0. 01 4. 028 4. 04

A little knowledge of material properties helps

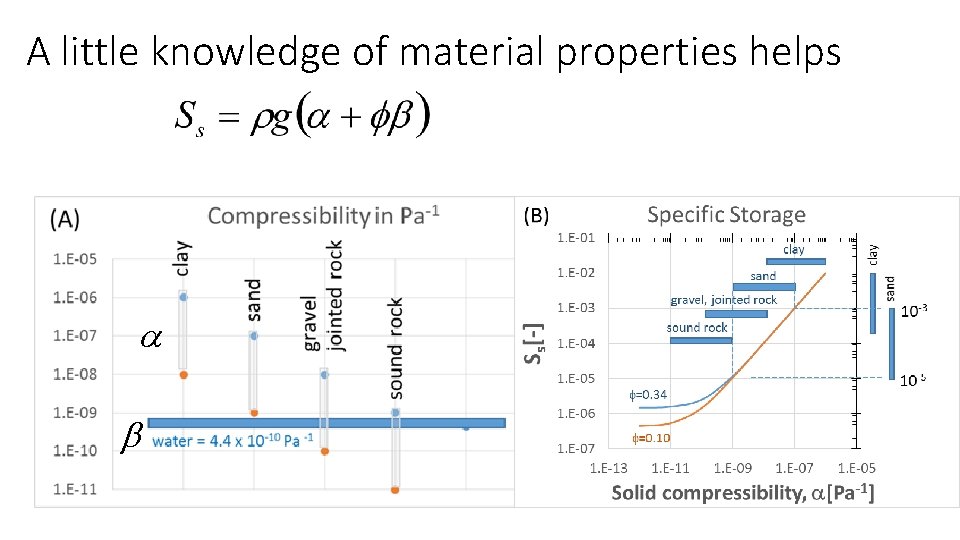
A little knowledge of material properties helps a b

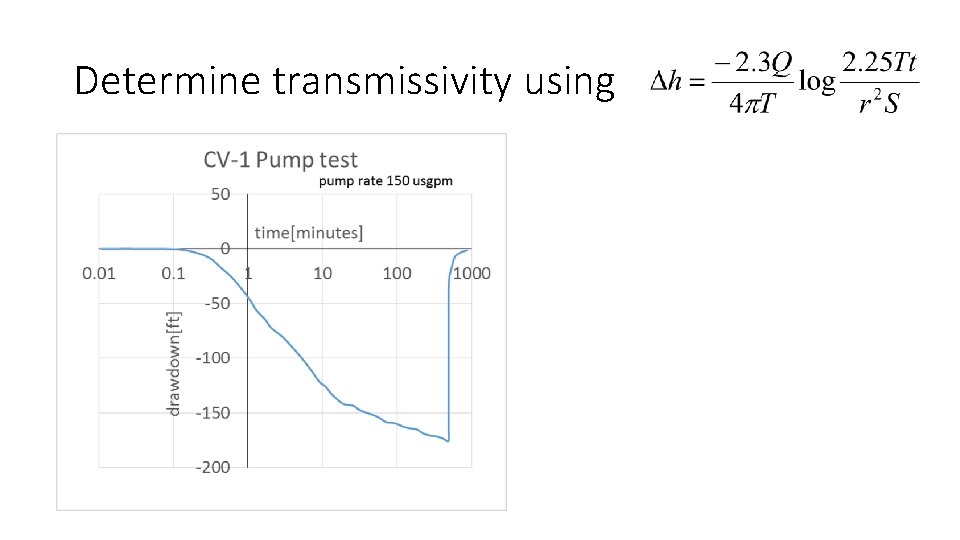
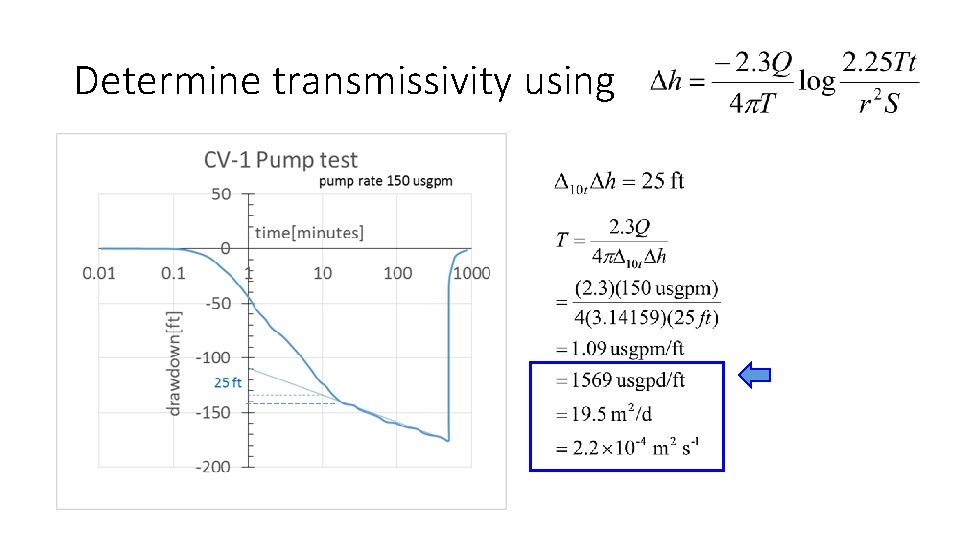
Determine transmissivity using

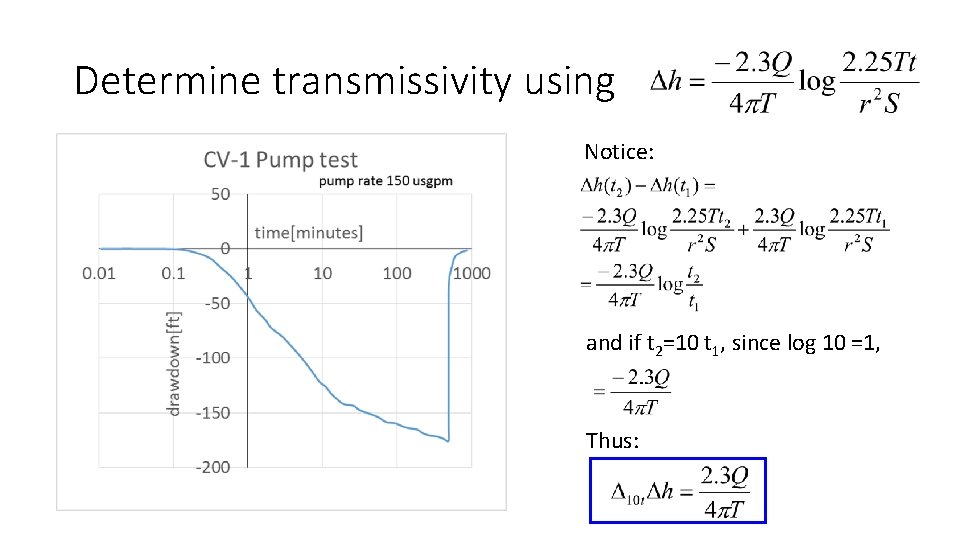
Determine transmissivity using Notice: and if t 2=10 t 1, since log 10 =1, Thus:

Determine transmissivity using

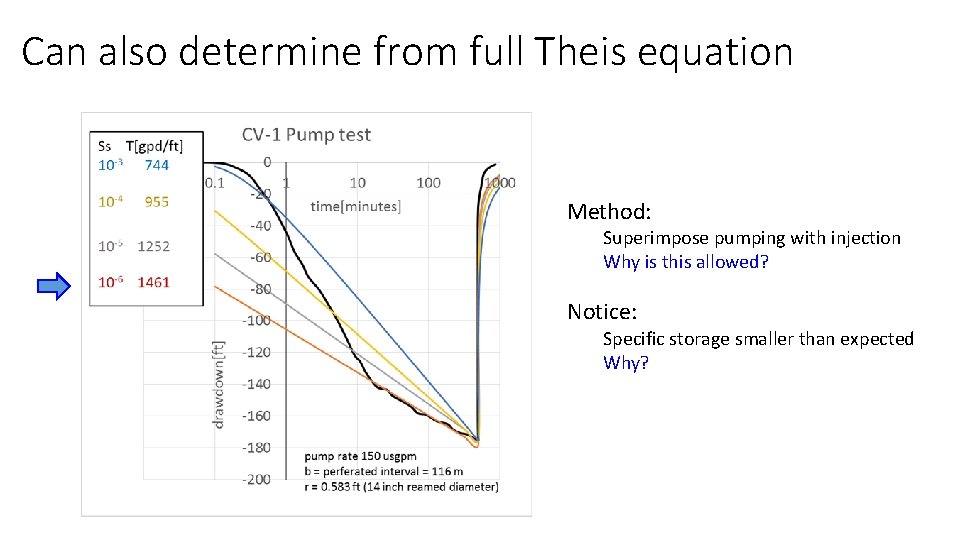
Can also determine from full Theis equation Method: Superimpose pumping with injection Why is this allowed? Notice: Specific storage smaller than expected Why?

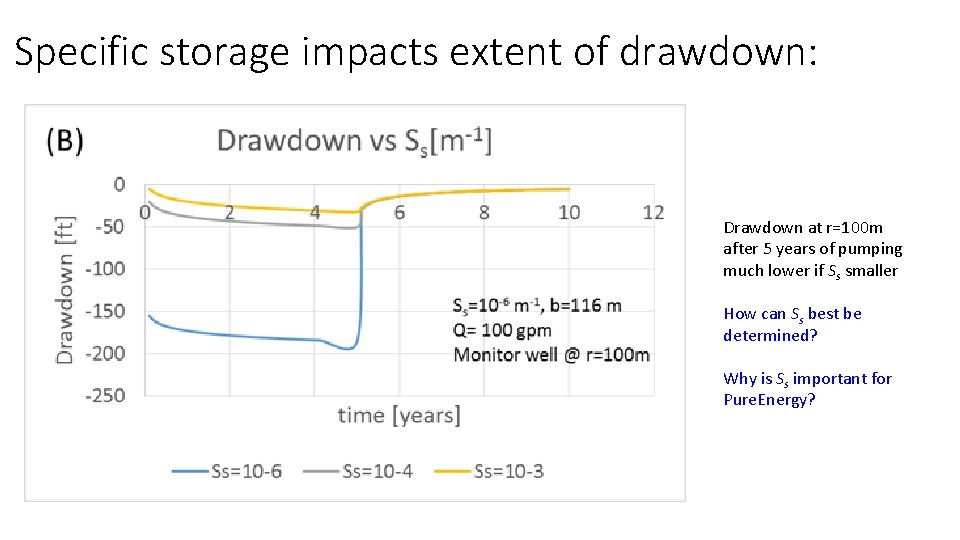
Specific storage impacts extent of drawdown: Drawdown at r=100 m after 5 years of pumping much lower if Ss smaller How can Ss best be determined? Why is Ss important for Pure. Energy?

Ss matters to permeability Ss 10 -6 10 -5 10 -4 10 -3 T[gpd/ft] 1461 1252 995 744 T[m 2/s] 2. 1 x 10 -4 1. 8 x 10 -4 1. 43 x 10 -4 1. 07 x 10 -4 K[m/s]=T/b 1. 8 x 10 -6 1. 6 x 10 -6 1. 2 x 10 -6 0. 9 x 10 -9 low specific storage high specific storage Formation is much less permeable if specific storage is high Does this make sense?

Determining storativity: Notice that if Dh=0, the log argument must =1, and Therefore extrapolate drawdown as a function of log distance to 0, determine ro, and use known values of t and T to determine S.

Specific storage impacts radius of influence: For: t=10 y = 31. 5 x 107 s T=1. 43 x 10 -4 m 2 s-1 Ss=10 -4 m-1 b=116 m S=1. 16 x 10 -2 ro=2. 95 km What would ro be for Ss=10 -6 m-1 ? Why would this matter to Pure. Energy?

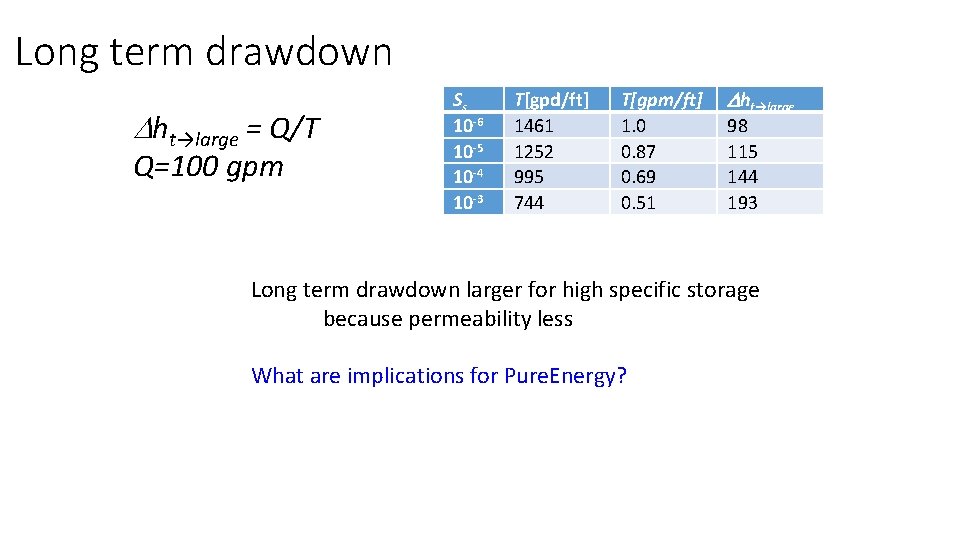
Long term drawdown Dht→large = Q/T Q=100 gpm Ss 10 -6 10 -5 10 -4 10 -3 T[gpd/ft] 1461 1252 995 744 T[gpm/ft] 1. 0 0. 87 0. 69 0. 51 Dht→large 98 115 144 193 Long term drawdown larger for high specific storage because permeability less What are implications for Pure. Energy?

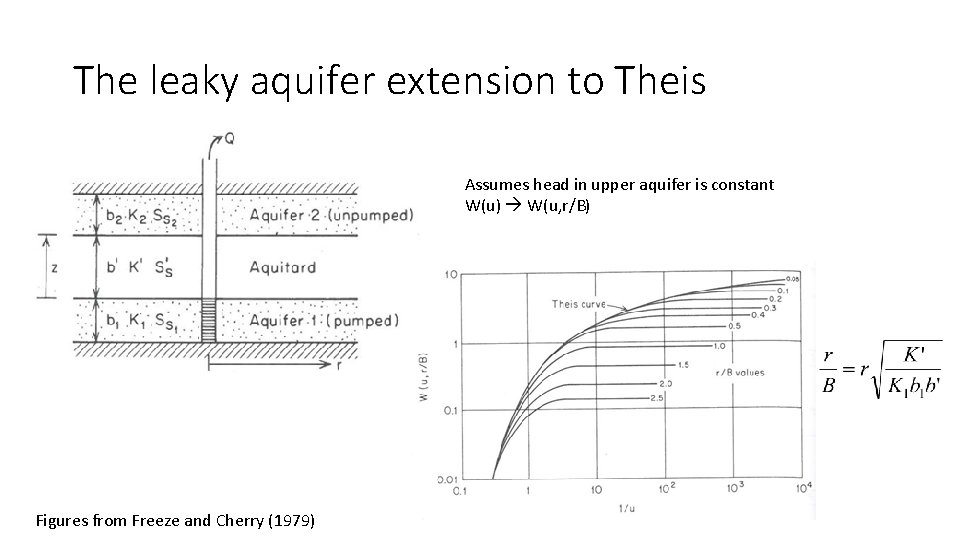
The leaky aquifer extension to Theis Assumes head in upper aquifer is constant W(u) W(u, r/B) Figures from Freeze and Cherry (1979)

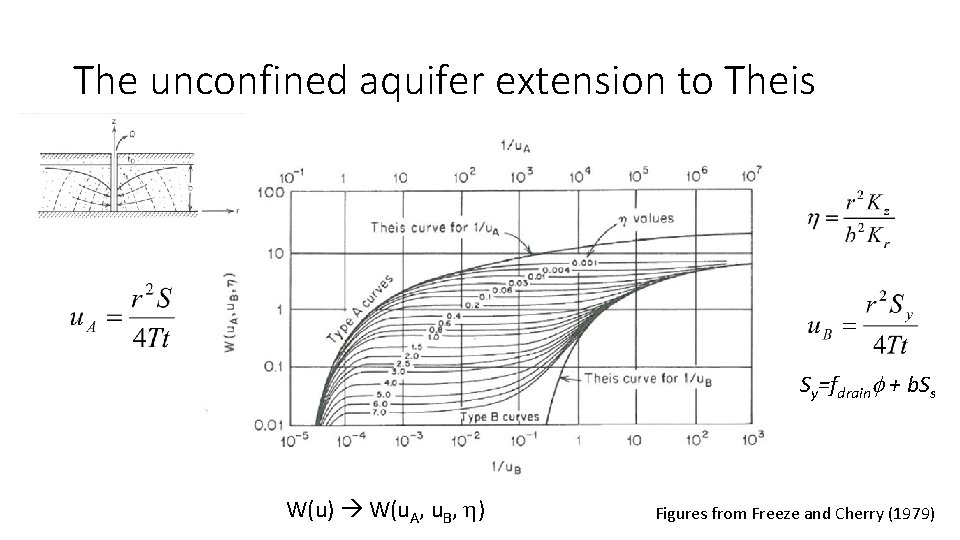
The unconfined aquifer extension to Theis Sy=fdrainf + b. Ss W(u) W(u. A, u. B, h) Figures from Freeze and Cherry (1979)

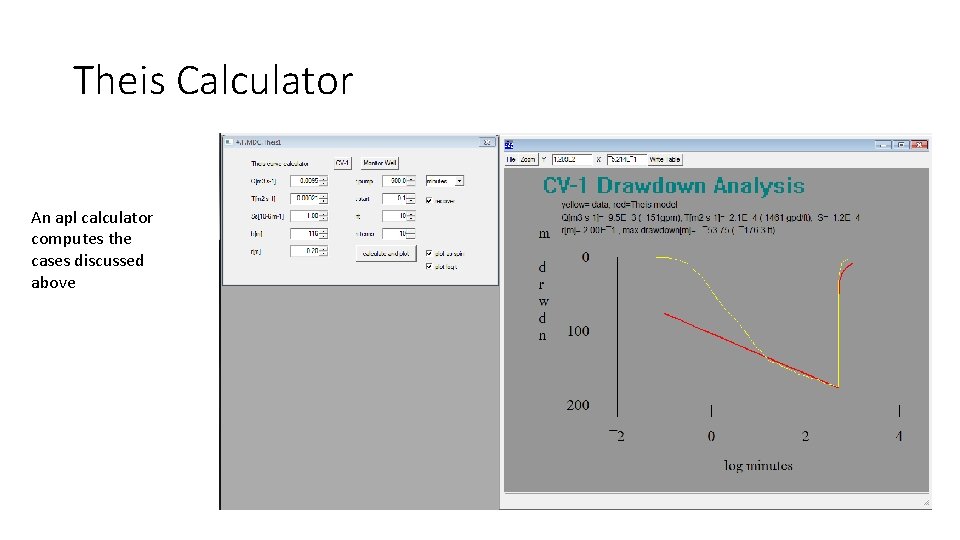
Theis Calculator An apl calculator computes the cases discussed above

The Well function program You all need to develop and maintain programming skills– python probably best

Questions • How realistic is the confined aquifer model? How far off could its suggestions be? What are the greatest risks?

Questions • How realistic is the confined aquifer model? How far off could its suggestions be? What are the greatest risks? • How many Petrel model runs do you think you would have to make to get the insights you have from this analytical approach? What does this suggest for modeling?

Questions • How realistic is the confined aquifer model? How far off could its suggestions be? What are the greatest risks? • How many Petrel model runs do you think you would have to make to get the insights you have from this analytical approach? What does this suggest for modeling? • Could you make a NPV calculation to assess what’s needed for Pure. Energy success?

Problem set #2

PS 2 Solutions L. M. Cathles 2017

(8 d)

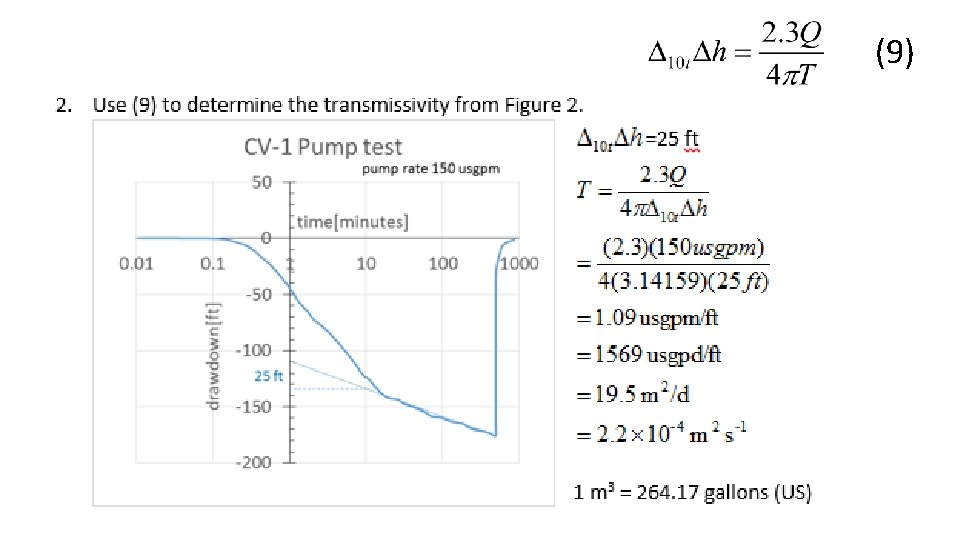
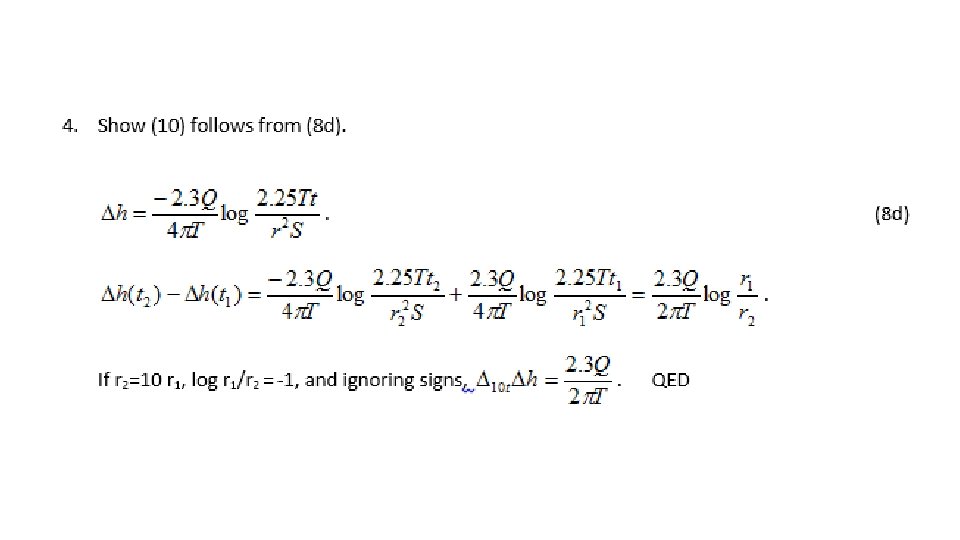
(10)

(12)

(13)