Lecture 2 Perfect Ciphers in Theory not Practice

Lecture 2: Perfect Ciphers (in Theory, not Practice) Shannon was the person who saw that the binary digit was the fundamental element in all of communication. That was really his discovery, and from it the whole communications revolution has sprung. R G Gallager I just wondered how things were put together. Claude Shannon CS 588: Cryptology University of Virginia 25 January 2005 Computer Science Claude Shannon, 1916 -2001 University of Virginia CS 588 David Evans http: //www. cs. virginia. edu/evans

Menu • Survey Results • Perfect Ciphers • Entropy and Unicity 25 January 2005 University of Virginia CS 588 2

Survey Responses • Majors: Cognitive Science, Computer Science (13), Computer Engineering (2), Economics, Math • Year: Third year: 6, Fourth Year: 10, Grad: 1, 2005: 1 • Midterm: March 3: 12, March 15: 3, March 17: 2, March 22: 1 • Broken in? : No: 13, Yes: 5 Full answers are on the course web site 25 January 2005 University of Virginia CS 588 3

What was the coolest thing you learned last semester? “i've been sitting here for like five minutes trying to think of something. perhaps that aristotle (or perhaps plato) hates bands that sell out. ” “hmm. . I learned there was a huge molasses explosion at the Boston harbor in the early 20 th century. . not really all that cool i guess because a lot of people died but still pretty interesting. ” 25 January 2005 University of Virginia CS 588 4

Break In Story In high-school the administrators installed a fairly restrictive rights-control program called "Fool. Proof". It was so restrictive, however, that my AP Comp. Sci class was unable to compile and run programs on the main HD forcing us to use a floppy disk for our source and intermediate files, which was painfully slow as projects increased in size. Having unsuccessfully lobbied to have restrictions lifted so we could compile and run programs on a temporary directory. I tried to convince them that there were more eloquent and flexible security programs out there. So, I did a little research on the version of Fool. Proof being used. It turns out that this version of Fool. Proof had two major security flaws: 25 January 2005 University of Virginia CS 588 5

Break In Story 1) A "backdoor" password used by tech support that is hardcoded into the executable and 2) The password information is stored in plaintext within main memory some number of bytes into one of its main data structures which was marked by an ascii string which was some sort of constant containing the version information. So, I acquired a utility which would allow me to browse and search the contents of physical memory determined what this ascii string would be for the given version of Fool. Proof and searched memory. Sure enough I came up with a match and about 8 bytes later a plaintext ascii string: "What. AFool" 25 January 2005 University of Virginia CS 588 6

Polling Protocol 25 January 2005 University of Virginia CS 588 7

Last Time • Big keyspace is not necessarily a strong cipher • Claim: One-Time Pad is perfect cipher – In theory: depends on perfectly random key, secure key distribution, no reuse – In practice: usually ineffective (VENONA, Lorenz Machine) • Today: what does is mean to be a perfect cipher? 25 January 2005 University of Virginia CS 588 8

Ways to Convince • “I tried really hard to break my cipher, but couldn’t. I’m a genius, so I’m sure no one else can break it either. ” • “Lots of really smart people tried to break it, and couldn’t. ” • Mathematical arguments – key size (dangerous!), statistical properties of ciphertext, depends on some provably (or believed) hard problem • Invulnerability to known cryptanalysis techniques (but what about undiscovered techniques? ) • Show that ciphertext could match multiple reasonable plaintexts without knowing key • Simple monoalphabetic secure for about 10 letters of English: XBCF CF FWPHGW This is secure Spat at troner 25 January 2005 University of Virginia CS 588 9

Claude Shannon • Master’s Thesis [1938] – boolean algebra in electronic circuits • “Mathematical Theory of Communication” [1948] – established information theory • “Communication Theory of Secrecy Systems” [1945/1949] (linked from notes) • Invented rocket-powered Frisbee, could juggle four balls while riding unicycle 25 January 2005 University of Virginia CS 588 10

Entropy Amount of information in a message: n H(M) = Prob [M ] log ([1 / Prob [M ] ) i i i=1 over all possible messages Mi 25 January 2005 University of Virginia CS 588 11

Entropy If there are n equally probable messages, n H(M) = 1/n log n i=1 = n * (1/n log n)) = log n Base of log is alphabet size, so for binary: H(M) = log 2 n where n is the number of possible meanings 25 January 2005 University of Virginia CS 588 12

Entropy Example M = months of the year H(M) = log 2 12 3. 6 (need 4 bits to encode a year) 25 January 2005 University of Virginia CS 588 13

Rate • Absolute rate: how much information can be encoded R = log 2 Z REnglish = (Z=size of alphabet) log 2 26 4. 7 bits / letter • Actual rate of a language: r = H(M) / N M is a source of N-letter messages r of months spelled out using 8 -bit ASCII: = log 2 12 / (8 letters * 8 bits/letter) 0. 06 25 January 2005 University of Virginia CS 588 14

Rate of English • r(English) is about. 28 letters/letter (1. 3 bits/letter) [Book uses 1. 5] – How can one estimate this? • How many meaningful 20 -letter messages in English? r = H(M) / N. 28 = H(M)/20 H(M) = 5. 6 = log 26 n n = 265. 6 ~ 83 million (of 2*1028 possible) Probability that 20 -letters are sensible English is About 1 in 2 * 1020 25 January 2005 University of Virginia CS 588 15

Redundancy • Redundancy (D) is defined: D=R–r • Redundancy in English: D = 1 -. 28 =. 72 letters/letter D = 4. 7 – 1. 3 = 3. 4 bits/letter Each letter is 1. 3 bits of content, and 3. 4 bits of redundancy. (~72%) • 7 -bit ASCII (as in PS 1, problem 5) D = 7 – 1. 3 = 5. 7 81% redundancy, 19% information 25 January 2005 University of Virginia CS 588 16

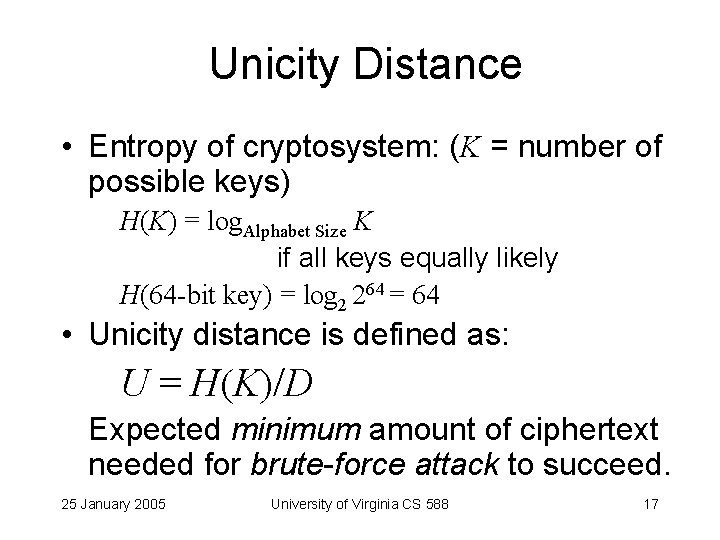
Unicity Distance • Entropy of cryptosystem: (K = number of possible keys) H(K) = log. Alphabet Size K if all keys equally likely H(64 -bit key) = log 2 264 = 64 • Unicity distance is defined as: U = H(K)/D Expected minimum amount of ciphertext needed for brute-force attack to succeed. 25 January 2005 University of Virginia CS 588 17

Unicity Examples • Monoalphabetic Substitution H(K) = log 2 26! 87 D = 3. 4 (redundancy in English) U = H(K)/D 25. 5 Intuition: if you have 25 letters, probably only matches one possible plaintext. D = 0 (random bit stream) U = H(K)/D = infinite 25 January 2005 University of Virginia CS 588 18

Unicity Distance • Probabilistic measure of how much ciphertext is needed to determine a unique plaintext • Does not indicate how much ciphertext is needed for cryptanalysis • If you have less than unicity distance ciphertext, can’t tell if guess is right. • As redundancy approaches 0, hard to cryptanalyze even simple cipher. 25 January 2005 University of Virginia CS 588 19

Shannon’s Theory [1945] Message space: { M 1, M 2, . . . , Mn } Assume finite number of messages Each message has probability p(M 1) + p(M 2) +. . . + p(Mn) = 1 Key space: { K 1, K 2, . . . , Kl } (Based on Eli Biham’s notes) 25 January 2005 University of Virginia CS 588 20

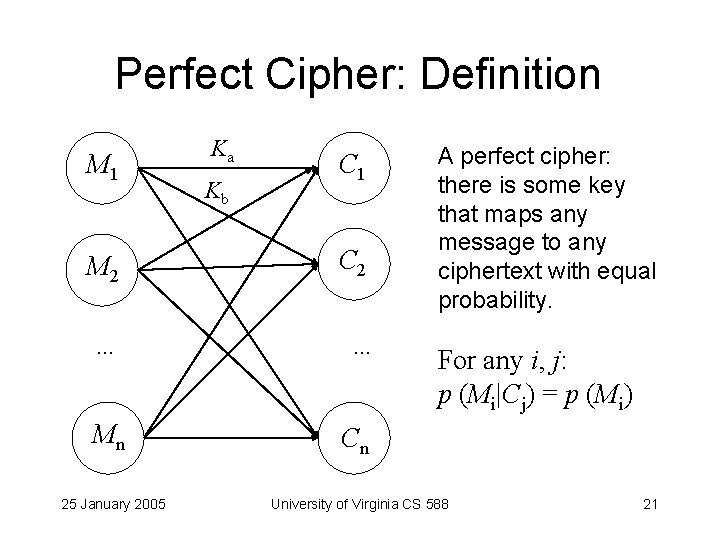
Perfect Cipher: Definition M 1 Ka Kb C 1 M 2 C 2 . . . Mn 25 January 2005 A perfect cipher: there is some key that maps any message to any ciphertext with equal probability. For any i, j: p (Mi|Cj) = p (Mi) Cn University of Virginia CS 588 21

Conditional Probability Prob [B | A] = The probability of B, given that A occurs Prob [ coin flip is tails ] = ½ Prob [ coin flip is tails | last coin flip was heads ] =½ Prob [ today is Monday | yesterday was Sunday] =1 Prob [ today is a weekend day | yesterday was a workday] = 1/5 25 January 2005 University of Virginia CS 588 22

Calculating Conditional Probability P [B | A ] = Prob [ A B ] Prob [ A ] Prob [ coin flip is tails | last coin flip was heads ] = Prob [ coin flip is tails and last coin flip was heads ] Prob [ last coin flip was heads ] = (½ * ½) / ½ = ½ 25 January 2005 University of Virginia CS 588 23

P (today is a weekend day | yesterday was a workday) = P (today is a weekend day and yesterday was a workday) / P (yesterday was a workday) = P (today is a weekend day) * P(yesterday was a workday) / P (yesterday was a workday) = 2/7 * 5/7 / 5/7 = 2/7 Wrong! P(A B) = P(A) * P(B) only if A and B are independent events 25 January 2005 University of Virginia CS 588 24

Perfect Cipher Definition: i, j: P (Mi|Cj) = P (Mi) A cipher is perfect iff: M, C P (C | M) = P (C) Or, equivalently: M, C P (M | C) = P (M) 25 January 2005 University of Virginia CS 588 25

Perfect Cipher M, C P (C | M) = P (C) M, C P (C) = K P(K) such that EK(M) = C Or: C P(K) K is independent of M such that EK(M) = C Without knowing anything about the key, any ciphertext is equally likely to match any plaintext. 25 January 2005 University of Virginia CS 588 26

Example: Monoalphabetic • Random monoalphabetic substitution for one letter message: C, M: P (C) = P (C | M) = 1/26. 25 January 2005 University of Virginia CS 588 27

Example: One-Time Pad For each bit: P(Ci = 0) = P(Ci = 0 | Mi = 0) = P (Ci = 0 | Mi = 1) = ½ since Ci = Ki Mi P (Ki Mi = 0) = P (Ki = 1) * P (Mi = 1) + P (Ki = 0) * P (Mi = 0) Truly random K means P (Ki = 1) = P (Ki = 0) = ½ * P (Mi = 1) + ½ * P (Mi = 0) = ½ * (P (Mi = 1) + P (Mi = 0)) = ½ All key bits are independent, so: P(C) = P(C | M) QED. 25 January 2005 University of Virginia CS 588 28

Perfect Cipher Keyspace Theorem: If a cipher is perfect, there must be at least as many keys (l) are there are possible messages (n). 25 January 2005 University of Virginia CS 588 29

Proof by Contradiction Suppose there is a perfect cipher with l < n. (More messages than keys. ) Let C 0 be some ciphertext with P(C 0) > 0. There exist m messages M such that M = DK(C 0 ) n - m messages M 0 such that M 0 DK(C 0 ) We know 1 m l < n so n - m > 0 and there is at least one message M 0. 25 January 2005 University of Virginia CS 588 30

Proof, cont. Consider the message M 0 where M 0 DK(C 0 ) for any K. So, P (C 0 | M 0) = 0. In a perfect cipher, P (C 0 | M 0) = P (C 0) > 0. Contradiction! It isn’t a perfect cipher. Hence, all perfect ciphers must have l n. 25 January 2005 University of Virginia CS 588 31

Example: Monoalphabetic Random monoalphabetic substitution is not a perfect cipher for messages of up to 20 letters: l = 26! n = 2620 l < n its not a perfect cipher. In previous proof, could choose C 0 = “AB” and M 0 = “ee” and P (C 0 | M 0) = 0. 25 January 2005 University of Virginia CS 588 32

Example: Monoalphabetic Is random monoalphabetic substitution a perfect cipher for messages of up to 2 letters? l = 26! l n. n = 262 No! Showing l n does not prove its perfect. 25 January 2005 University of Virginia CS 588 33

Summary • Cipher is perfect: i, j: p (Mi|Cj) = p (Mi) Given any ciphertext, the probability that it matches any particular message is the same. • Equivalently, i, j: p (Ci|Mj) = p (Ci) Given any plaintext, the probability that it matches any particular ciphertext is the same. 25 January 2005 University of Virginia CS 588 34

Imperfect Cipher • To prove a cipher is imperfect either: – Find a ciphertext that is more likely to be one message than another – Show that there are more messages than keys • Implies there is some ciphertext more likely to be one message than another even if you can’t find it. 25 January 2005 University of Virginia CS 588 35

Charge • Problem Set 1: due Feb 3 – All other questions covered (as much as we will cover them in class) already • Next time: – Classical ciphers (Nate Paul) 25 January 2005 University of Virginia CS 588 36