Lecture 2 Introduction to wave theory II Mathematical

Lecture 2: Introduction to wave theory (II) Mathematical description of waves (Y&F 15. 3): o Phase velocity: the velocity (speed) at which we would have to move to keep up with a point of constant phase on the wave. o Right moving wave: o Derivative with respect to t is zero: Phase velocity: is the same as speed of wave: o Transverse speed of wave: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 1

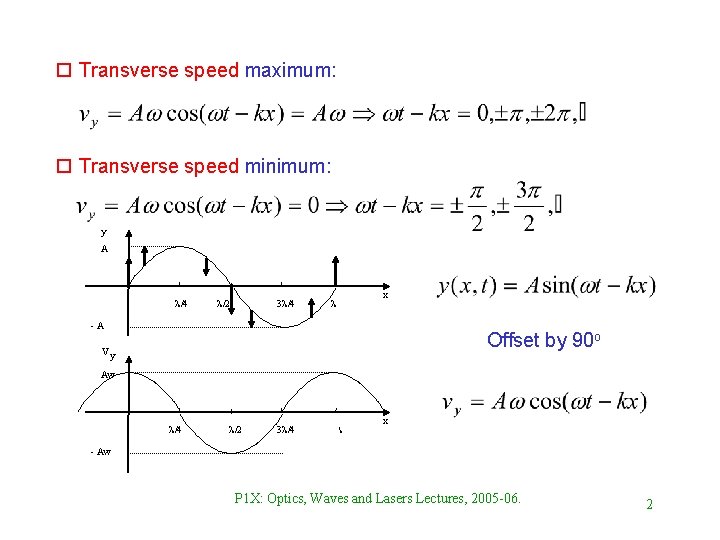
o Transverse speed maximum: o Transverse speed minimum: y A l/4 l/2 3 l/4 x l -A Offset by 90 o vy Aw l/4 l/2 3 l/4 l x - Aw P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 2

Example: 15 -2 from Y&F (page 556) Find the maximum transverse speed of the example shown in lecture 1. What is the velocity at t=0, at the end of the clothes-line and at 3. 0 m from the end. At x=t=0, velocity is maximum transverse speed = +0. 94 ms-1 At x=3. 0 m and t=0: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 3

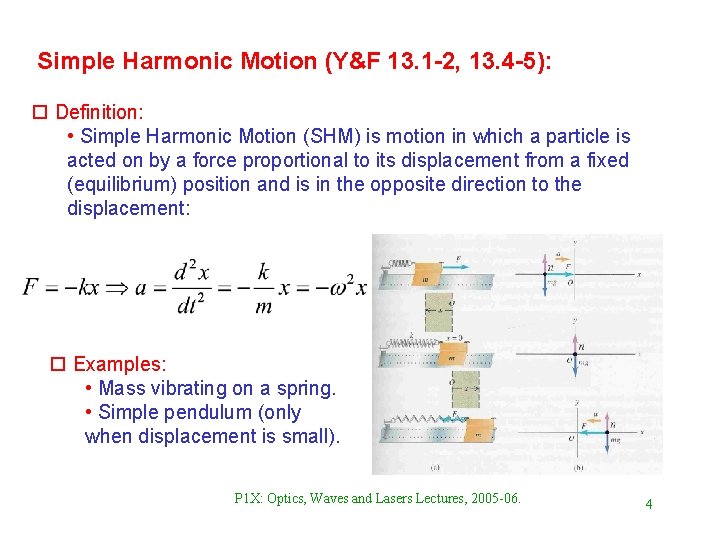
Simple Harmonic Motion (Y&F 13. 1 -2, 13. 4 -5): o Definition: • Simple Harmonic Motion (SHM) is motion in which a particle is acted on by a force proportional to its displacement from a fixed (equilibrium) position and is in the opposite direction to the displacement: o Examples: • Mass vibrating on a spring. • Simple pendulum (only when displacement is small). P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 4

o Simple pendulum: • Vertical: • Horizontal: If q is small then when and therefore: and: The same as the restoring force of a spring but with: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 5

o Solution: • What function satisfies ? • Try with x the angular frequency (rad/s): A • For the case of the spring: T/4 T/2 3 T/4 T t • For the case of the pendulum: -A P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 6

o. Definitions: a) Amplitude A is maximum displacement (m). b) Frequency f: number of oscillations per second. (Units: 1 Hertz = 1 cycle/s = 1 s-1) c) Period T: time (s) between oscillations d) Phase constant (f ): gives position of oscillation at t=0. P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 7

Example: 13 -2 from Y&F A spring is mounted horizontally. A force of 6. 0 N causes a displacement of 0. 030 m. If we attach an object of 0. 50 kg to the end and pull it a distance of 0. 020 m and watch it oscillate in SHM, find (a) the force constant of the spring, (b) the angular frequency, frequency and period of oscillation. (a) At x = 0. 030 m, F=-6. 0 N (b) m=0. 50 kg, k=200 N/m: The frequency: The period: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 8

Example: 13 -8 from Y&F Find the frequency and period of a simple pendulum that is 1. 0 m long (assume g=9. 80 m/s). The angular frequency: The period: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 9

Example: Vertical SHM Vertical oscillations from a spring hanging vertically. 1) At rest: Spring is stretched by Dl such that: 2) x above equilibrium: 3) x below equilibrium: Fnet Same SHM as in vertical case, oscillations with angular frequency: Equilibrium is at stretched position Dl instead of x=0 P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 10

Example: 13 -6 from Y&F Shock absorbers of an old car with mass 1000 kg are worn out. When a person weighing 100 kg climbs into the car, it sinks by 2. 8 cm. When the car is in motion and hits a bump it oscillates. What is the frequency and period of oscillation? The spring constant: The angular frequency: The period: P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 11

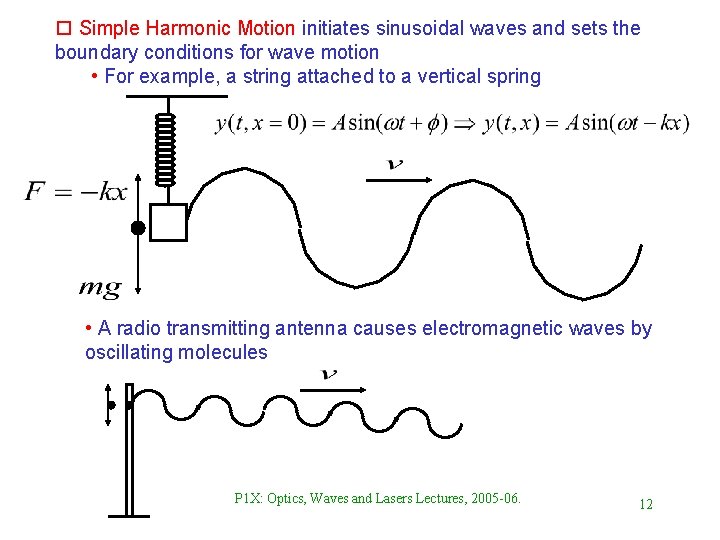
o Simple Harmonic Motion initiates sinusoidal waves and sets the boundary conditions for wave motion • For example, a string attached to a vertical spring • A radio transmitting antenna causes electromagnetic waves by oscillating molecules P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 12