Lecture 2 Goals Introduction to recursion Examples of

Lecture 2 Goals: • Introduction to recursion • Examples of recursive programs Reading: Chapter 1 of the text. Jan 23 -12

Recursion Recursive function • A function defined in terms of itself e. g. f(x)= 2 * f(x – 1) Recursive definition • a concept defined in terms of itself. e. g. an arithmetic expression is either a number, or is of the form X op Y where X and Y are arithmetic expressions and op is an operator.

Recursion Recursive data structure • a structure whose substructure is of the same type as the structure e. g. a binary tree is either a single node or a node with two children both of which are also binary trees. Recursive program • program that calls itself. int F(int x) { if (x == 1) return 1; else return 2 * F(x – 1); }

Recursion - rules Rule 1: Provide exit from recursion. (focus on base cases – some times, more than one base case is needed. ) Rule 2: Make sure that the successive recursive calls progress towards the base case. Rule 3: Assume that recursive calls work. Rule 4: Compound interest rule: Avoid redundant calls.

Recursion – simple examples 1) Compute n! n! = 1 x 2 … x n = (n – 1)! x n 2) Compute 1 + 2 + … + n f(n) = n + f(n – 1) 3) Compute the n-th Fibonacci number f(n) = f(n – 1) + f(n – 2)

Example: (from Chapter 2 of text) Given x and n, we want to compute xn. Obvious iterative solution: int exp_it(int x, int n) { int temp = x; for (int j= 1; j < n; ++j) temp*= x; return temp; } The number of multiplications performed is n – 1. We will see that a recursive algorithm provides a much faster solution. Faster algorithm is crucial for RSA encryption algorithm.

Idea behind the algorithm Rule of exponents: xn = (x 2)n/2 if n is even x * (x 2)(n-1)/2 if n is odd • base case n = 1 return x • even n call exp(x*x , n/2) and return the result. • odd n call exp(x*x, (n – 1)/2) and multiply the result of call by x and return the product.

Code for recursive exponent algorithm int exp_rec (int x, int n) { if (n == 1) return x; else if (n%2 == 0) return exp_rec(x*x, n/2); else return x* exp_rec(x*x, (n – 1)/2); } Efficiency of the algorithm: exp_it(x, 100000) would perform 99999 multiplications. But exp_rec(x, 100000) the recursive algorithm would perform only 21 multiplications.

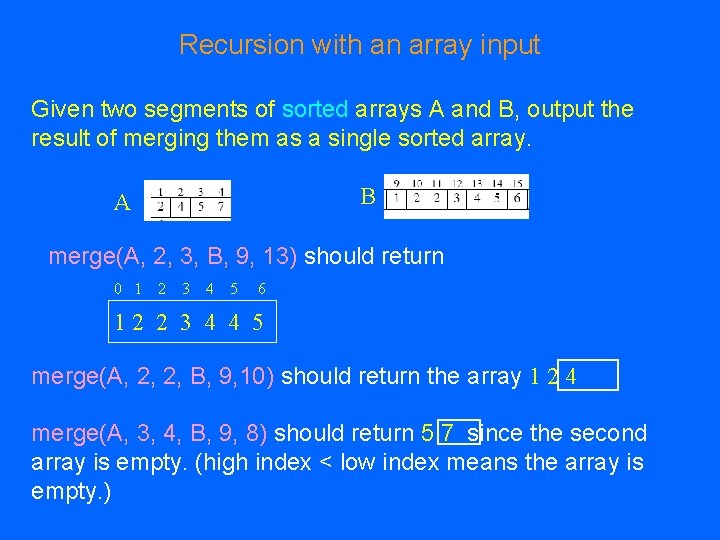
Recursion with an array input Given two segments of sorted arrays A and B, output the result of merging them as a single sorted array. B A merge(A, 2, 3, B, 9, 13) should return 0 1 2 3 4 5 6 12 2 3 4 4 5 merge(A, 2, 2, B, 9, 10) should return the array 1 2 4 merge(A, 3, 4, B, 9, 8) should return 5 7 since the second array is empty. (high index < low index means the array is empty. )

What are the base cases?

What are the base cases? • one array segment is empty. In this case, what is the output?

What are the base cases? • one array segment is empty. In this case, what is the output? • The other array segment, so we just have to copy the segment to the output.

What are the base cases? • one array segment is empty. In this case, what is the output? • The other array segment, so we just have to copy the segment to the output. • what if both segments are not empty? We need to make recursive call.

• Before we proceed, we need to make a change to the prototype of the function merge. • We will add two more parameters - the name of the array and the starting index in the output array at which we want to write.

A B merge(A, 2, 3, B, 9, 13, C, 3) should return 3 4 5 6 7 8 9 C 12 2 3 4 4 5

merge(A, low 1, high 1, B, low 2, high 2, C, low) A B Case 1: A[low 1] < B[low 2] Example: merge(A, 9, 13, B, 2, 3, C, 0) 0 1 2 3 4 5 6 C 12 2 3 4 4 5

merge(A, low 1, high 1, B, low 2, high 2, C, low) A B Case 1: A[low 1] < B[low 2] Example: merge(A, 9, 13, B, 2, 3, C, 0) Step 1: move A[low 1] to C[low]. Now a recursive call to merge will get the rest of the job done. What call? 0 1 2 3 4 5 6 12 2 3 4 4 5

merge(A, low 1, high 1, B, low 2, high 2) A B Case 1: A[low 1] < B[low 2] Example: merge(A, 9, 13, B, 2, 3, C, 0) Step 1: move A[low 1] to Out[0]. Now a recursive call to merge will get the rest of the job done. What call? merge(A, low 1+1, high 1, B, low 2, high 2, C, low + 1) 0 1 2 3 4 5 6 12 2 3 4 4 5

Case 2: A[low 1] > B[low 2]. Move B[low 2] to C[low] and make a recursive call to merge(A, low 1, high 1, B, low 2+1, high 2, C, low+1) The complete code is shown below:

void merge(int A[], int low 1, int high 1, int B[], int low 2, int high 2, int C[], int low) { if (high 1 < low 1) copy(B, low 2, high 2, C, low); else if (high 2 < low 2) copy(A, low 1, high 1, C, low); else if (A[low 1] < B[low 2]) {C[low] = A[low 1]; merge(A, low 1+1, high 1, B, low 2, high 2, C, low + 1); } else {C[low] = B[low 2]; merge(A, low 1, high 1, B, low 2+1, high 2, C, low + 1); } } void copy(int A[], int s, int t, int B[], int s 1) { for (int j= s; j<= t; ++j) B[s 1 +j - s] = A[j]; }