Lecture 2 CMOS Transistor Theory Original Lecture notes

Lecture 2: CMOS Transistor Theory Original Lecture notes © 2010 David Money Harris Modified by Konstantinos Tatas 3: CMOS Transistor Theory 1

Outline q q q Introduction MOS Capacitor n. MOS I-V Characteristics p. MOS I-V Characteristics Gate and Diffusion Capacitance 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 2

Introduction q So far, we have treated transistors as ideal switches q An ON transistor passes a finite amount of current – Depends on terminal voltages – Derive current-voltage (I-V) relationships q Transistor gate, source, drain all have capacitance – I = C (DV/Dt) -> Dt = (C/I) DV – Capacitance and current determine speed 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 3

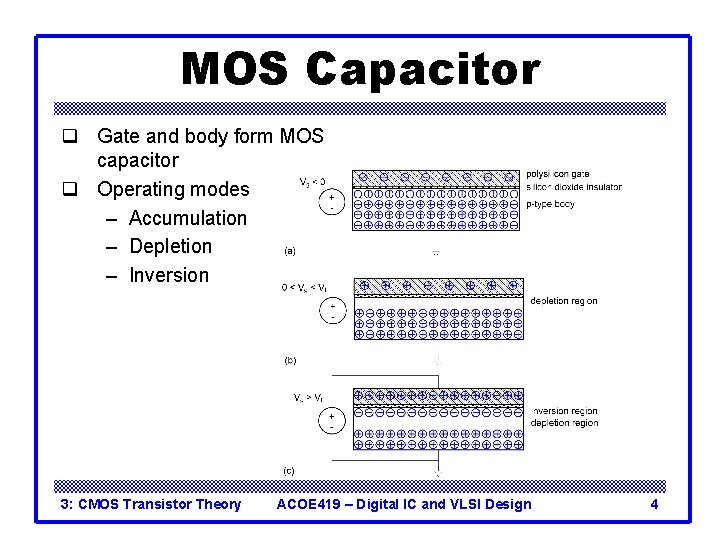
MOS Capacitor q Gate and body form MOS capacitor q Operating modes – Accumulation – Depletion – Inversion 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 4

Terminal Voltages q Mode of operation depends on Vg, Vd, Vs – Vgs = Vg – Vs – Vgd = Vg – Vds = Vd – Vs = Vgs - Vgd q Source and drain are symmetric diffusion terminals – By convention, source is terminal at lower voltage – Hence Vds 0 q n. MOS body is grounded. First assume source is 0 too. q Three regions of operation – Cutoff – Linear – Saturation 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 5

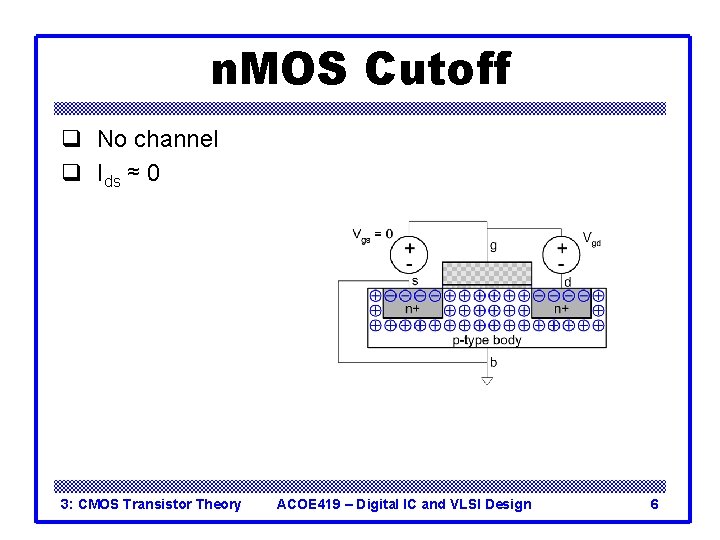
n. MOS Cutoff q No channel q Ids ≈ 0 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 6

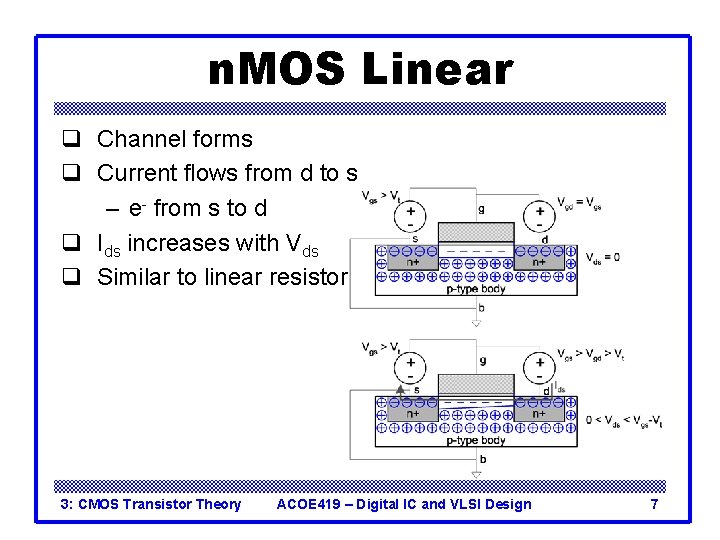
n. MOS Linear q Channel forms q Current flows from d to s – e- from s to d q Ids increases with Vds q Similar to linear resistor 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 7

n. MOS Saturation q q Channel pinches off Ids independent of Vds We say current saturates Similar to current source 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 8

I-V Characteristics q In Linear region, Ids depends on – How much charge is in the channel? – How fast is the charge moving? 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 9

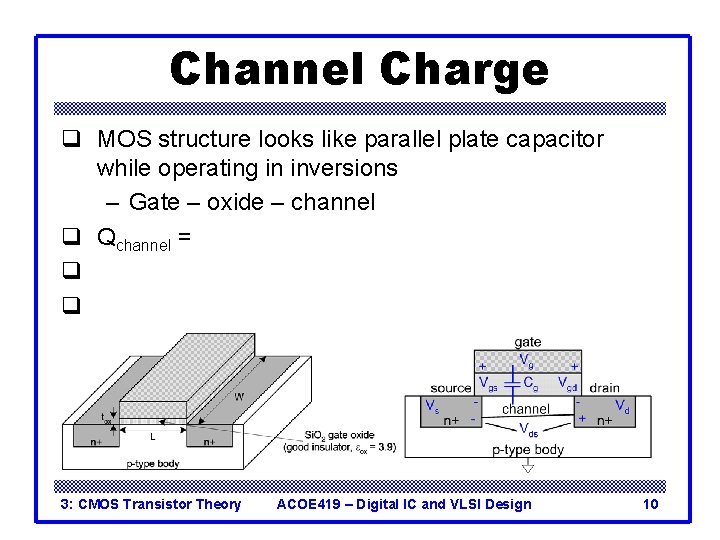
Channel Charge q MOS structure looks like parallel plate capacitor while operating in inversions – Gate – oxide – channel q Qchannel = CV Cox = eox / tox q C = Cg = eox. WL/tox = Cox. WL q V = Vgc – Vt = (Vgs – Vds/2) – Vt 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 10

Carrier velocity q Charge is carried by eq Electrons are propelled by the lateral electric field between source and drain – E = Vds/L q Carrier velocity v proportional to lateral E-field – v = m. E m called mobility q Time for carrier to cross channel: – t=L/v 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 11

n. MOS Linear I-V q Now we know – How much charge Qchannel is in the channel – How much time t each carrier takes to cross 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 12

n. MOS Saturation I-V q If Vgd < Vt, channel pinches off near drain – When Vds > Vdsat = Vgs – Vt q Now drain voltage no longer increases current 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 13

n. MOS I-V Summary q Shockley 1 st order transistor models 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 14

Example q We will be using a 0. 6 mm process for your project – From AMI Semiconductor – tox = 100 Å – m = 350 cm 2/V*s – Vt = 0. 7 V q Plot Ids vs. Vds – Vgs = 0, 1, 2, 3, 4, 5 – Use W/L = 4/2 l 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 15

p. MOS I-V q All dopings and voltages are inverted for p. MOS – Source is the more positive terminal q Mobility mp is determined by holes – Typically 2 -3 x lower than that of electrons mn – 120 cm 2/V • s in AMI 0. 6 mm process q Thus p. MOS must be wider to provide same current – In this class, assume mn / mp = 2 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 16

Capacitance q Any two conductors separated by an insulator have capacitance q Gate to channel capacitor is very important – Creates channel charge necessary for operation q Source and drain have capacitance to body – Across reverse-biased diodes – Called diffusion capacitance because it is associated with source/drain diffusion 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 17

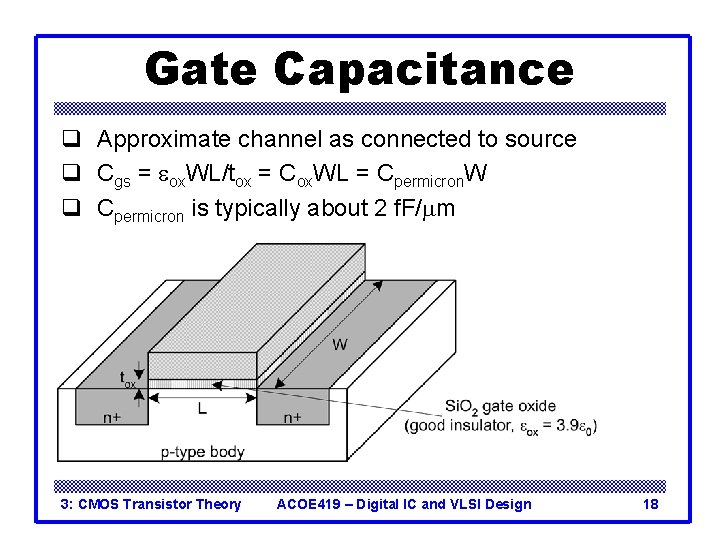
Gate Capacitance q Approximate channel as connected to source q Cgs = eox. WL/tox = Cox. WL = Cpermicron. W q Cpermicron is typically about 2 f. F/mm 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 18

Diffusion Capacitance q Csb, Cdb q Undesirable, called parasitic capacitance q Capacitance depends on area and perimeter – Use small diffusion nodes – Comparable to Cg for contacted diff – ½ Cg for uncontacted – Varies with process 2: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 19

Example 1 q Consider an n. MOS transistor in a 0. 6 μm process with W/L = 4/2λ. In this process, the gate oxide thickness is 100 Å and the mobility of electrons is 350 cm^2/V · s. Give the Ids equation for the linear and saturation regions 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 20

Example 2 q A 90 nm long transistor has a gate oxide thickness of 16 Å. What is its gate capacitance per micron of width? 3: CMOS Transistor Theory ACOE 419 – Digital IC and VLSI Design 21